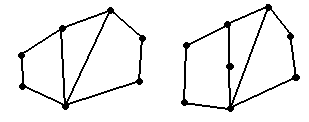
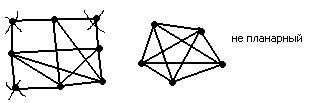
- •Теория графов
- •Деревья
- •Определения
- •Основные свойства деревьев
- •Ориентированные деревья
- •Деревья покрытия. Остовы
- •Раскраска графов
- •Алгоритм правильной раскраски
- •П ланарность
- •Плоские и планарные графы
- •Грани плоского графа. Формула Эйлера
- •Теорема Потрягина-Куратовского
- •Алгоритм укладки графа на плоскости
- •Алгоритм укладки графа на плоскости
-
Теорема Потрягина-Куратовского
Введем операцию подразбиения ребра
![]() графа. Она состоит в следующем: из графа
удалятся ребро
графа. Она состоит в следующем: из графа
удалятся ребро
![]() и добавляются два новых ребра
и добавляются два новых ребра
![]() и
и
![]() ,
где
,
где
![]() новая вершина.
новая вершина.
-
2 графа называются гомеоморфными, если оба они могут быть получены из одного и того же графа подразбиением его рёбер.
Если граф планарный, то любой гомеоморфный ему граф также является планарным.
Исторически первым критерием планарности графов является критерий, доказанный Потрягиным (1927) и Куратовским (1930) независимо друг от друга.
-
Потрягина-Куратовского: Граф планарен т.и.т.т., когда он не содержит подграфов, гомеоморфных К5 или К3,3.
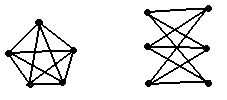 К5
К3,3
К5
К3,3
Без доказательства.
-
Алгоритм укладки графа на плоскости
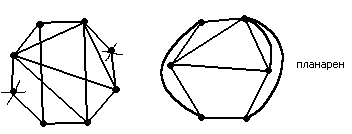
Рассмотренный выше критерий планарности таков, что если даже удалось установить планарность, то нет информации о том, как строить его укладку на плоскости (т.е., как его расположить на плоскости без пересечения рёбер).
В то же время, при решении практических задач недостаточно знать, что граф планарен, а необходимо построить его плоское изображение.
Всё это вызвало появление алгоритмов,
которые не только проверяют граф на
планарность, но и строят его плоскую
укладку, если это возможно. Рассмотрим
один из этих алгоритмов.
![]() .
.
Введем ряд определений.
-
Пусть построена некоторая укладка подграфа
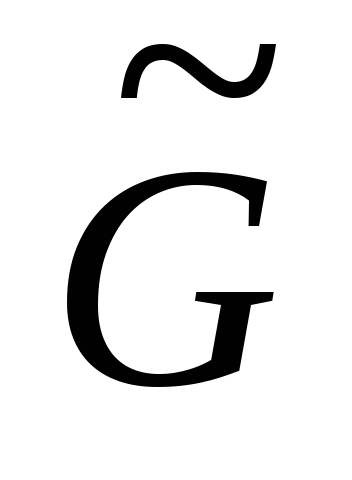 графа
графа
 .
Сегментом
.
Сегментом
 относительно
относительно
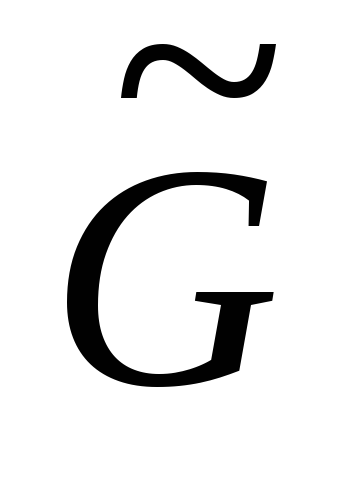 (или просто сегментом) будем называть
подграф графа
(или просто сегментом) будем называть
подграф графа
 одного из двух видов:
одного из двух видов:
-
Ребро
 такое, что
такое, что
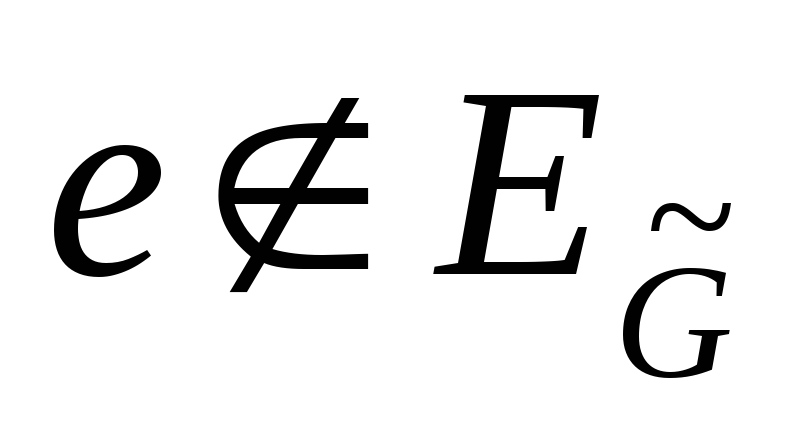 ,
,
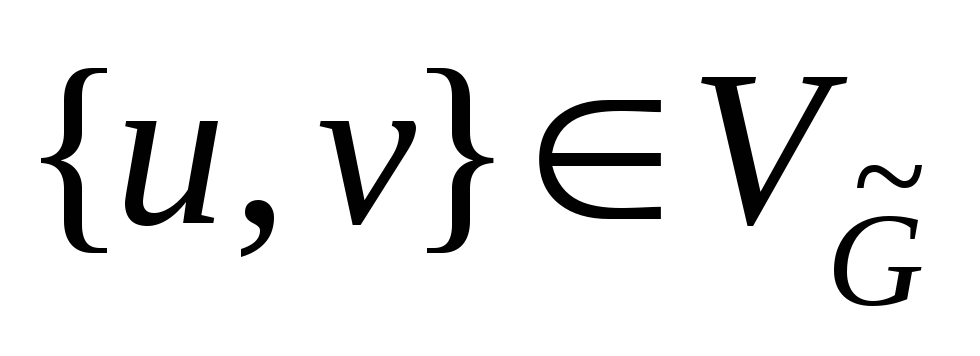 ;
; -
Компоненту связности графа
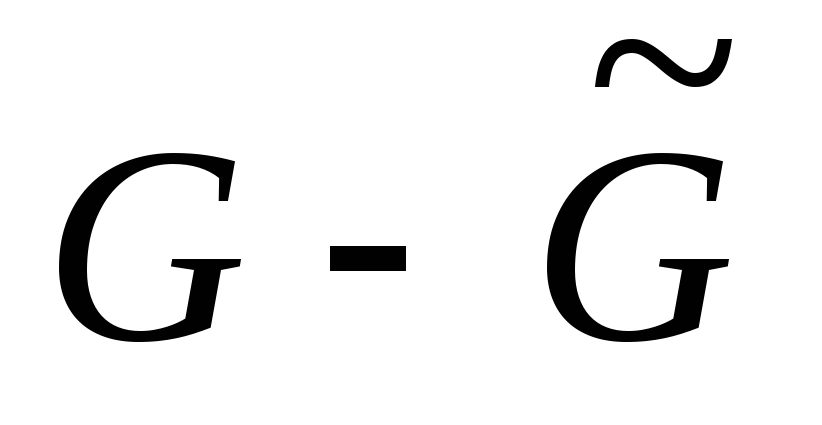 ,
дополненную всеми рёбрами графа
,
дополненную всеми рёбрами графа
 ,
инцидентными ее вершинам (взятой
компоненты), и концами этих рёбер.
,
инцидентными ее вершинам (взятой
компоненты), и концами этих рёбер.
-
Вершину
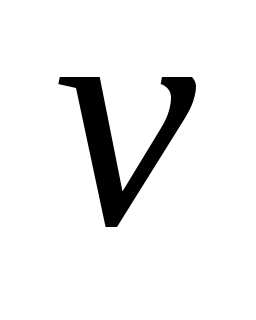 сегмента
сегмента
 относительно
относительно
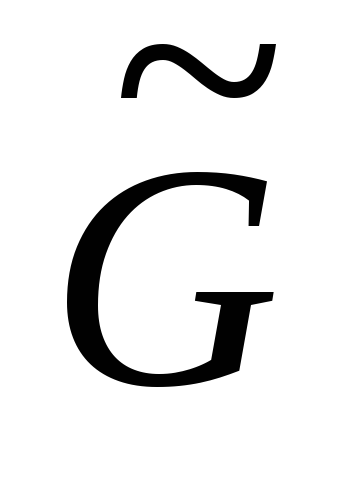 будем
называть контактной, если
будем
называть контактной, если
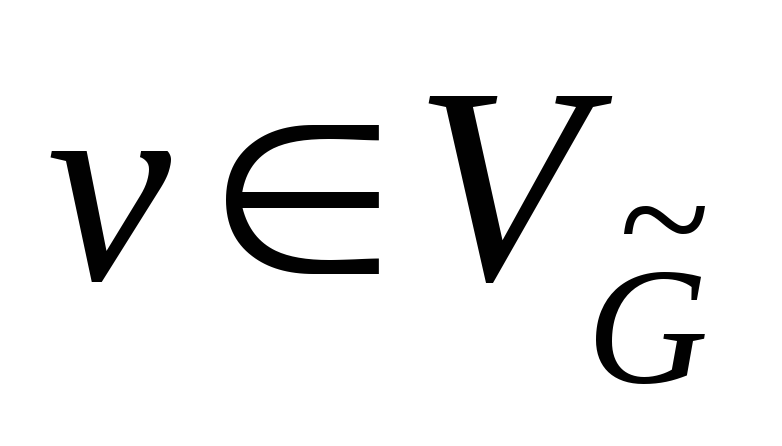 .
.

![]()
![]()
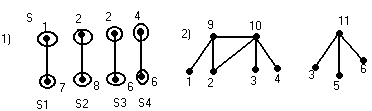
-
Т.к.
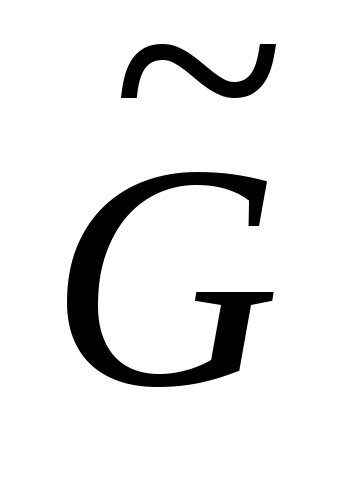 плоский, то он разбивает плоскость на
грани. Допустимой гранью для сегмента
плоский, то он разбивает плоскость на
грани. Допустимой гранью для сегмента
 относительно
относительно
 называется грань
называется грань
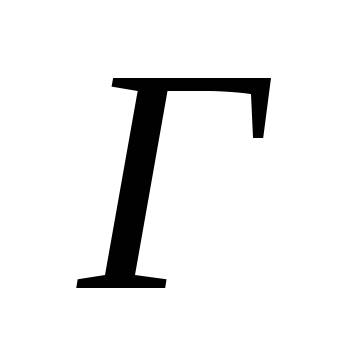 графа
графа
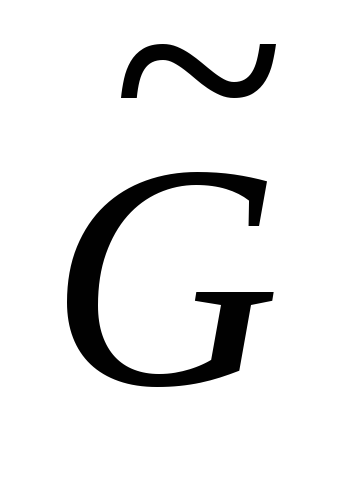 ,
содержащая все контактные вершины
сегмента
,
содержащая все контактные вершины
сегмента
 .
.
Через
![]() будем обозначать множество допустимых
граней для
будем обозначать множество допустимых
граней для
![]() .
Может оказаться, что
.
Может оказаться, что
![]() .
.
-
Простую цепь
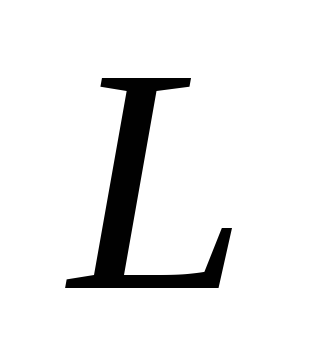 сегмента
сегмента
 ,
соединяющие две различные контактные
вершины и не содержащих других контактных
вершин, назовём
,
соединяющие две различные контактные
вершины и не содержащих других контактных
вершин, назовём
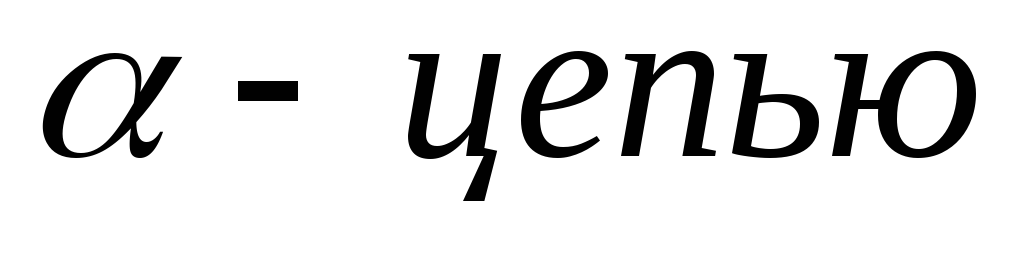 .
.
Алгоритм укладки графа на плоскости
-
Выберем некоторый простой цикл
 графа
графа
 и уложим его на плоскости. Положим
и уложим его на плоскости. Положим
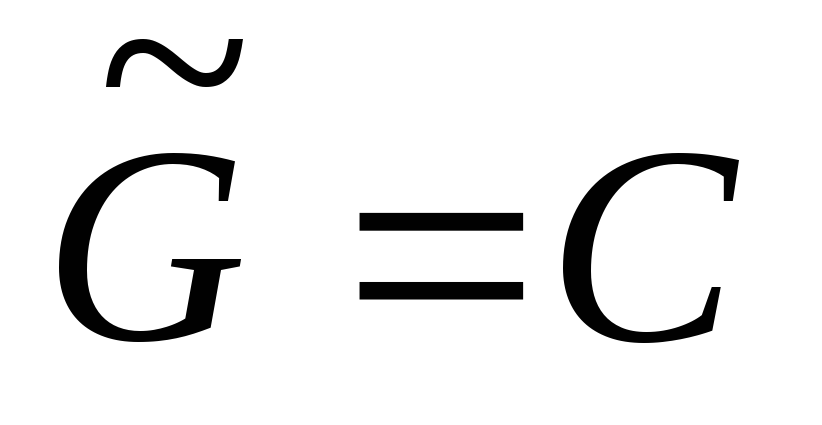 .
. -
Найдем грани
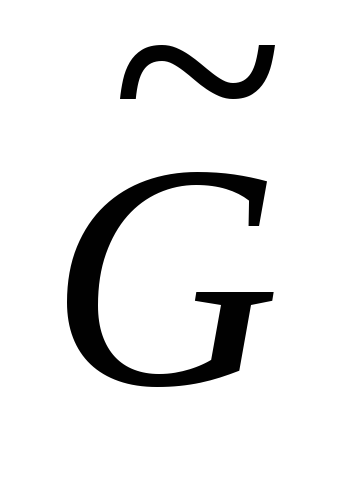 и сегменты относительно
и сегменты относительно
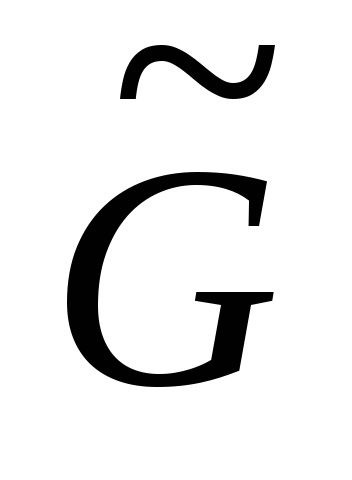 .
Если множество сегментов пусто, то
перейти к п.7.
.
Если множество сегментов пусто, то
перейти к п.7. -
Для каждого сегмента
 определим множество
определим множество
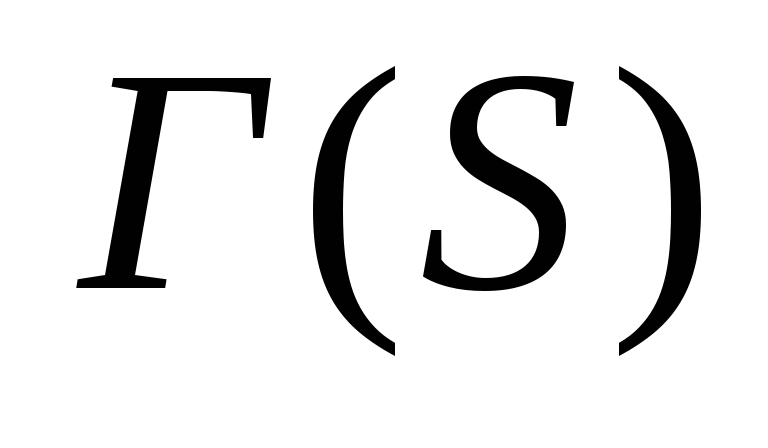 .
. -
Если
 сегмент
сегмент
 ,
для которого
,
для которого
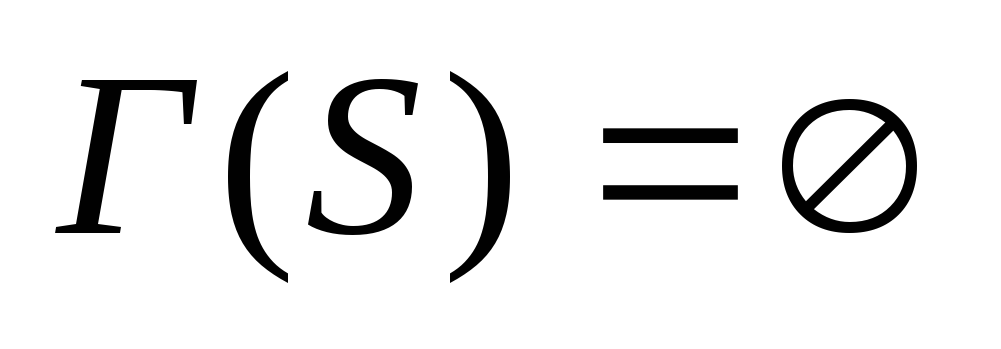
-
Если
 сегмент
сегмент
 ,
для которого имеется единственная
грань
,
для которого имеется единственная
грань
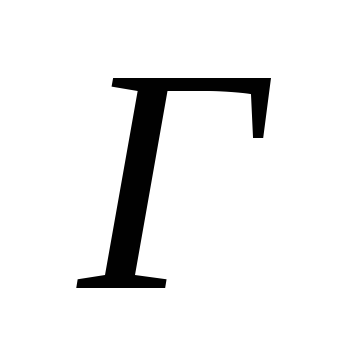 ,
то перейдём к п.6. Иначе к п.5
,
то перейдём к п.6. Иначе к п.5 -
Для некоторого сегмента
 выбираем
произвольно допустимую грань
выбираем
произвольно допустимую грань
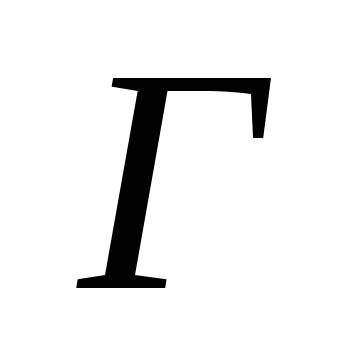 .
. -
Поместим произвольную
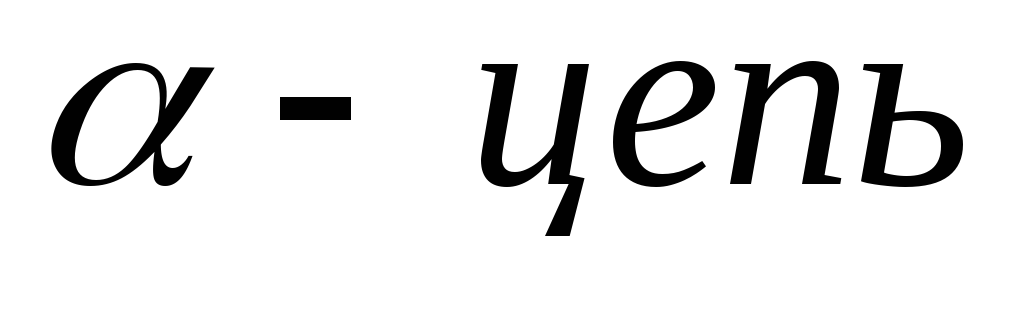
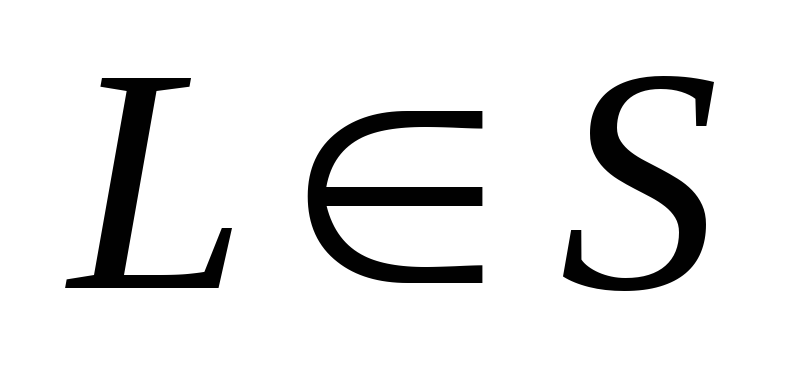 в грань
в грань
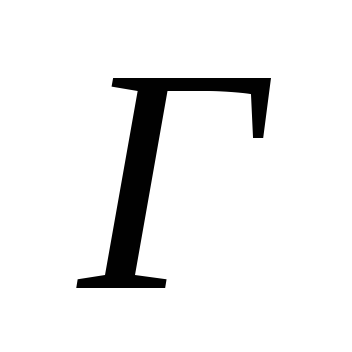 ;
заменим
;
заменим
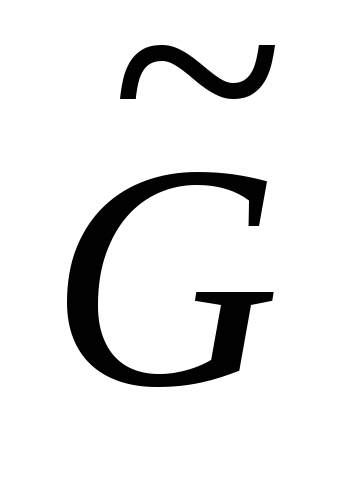 на
на
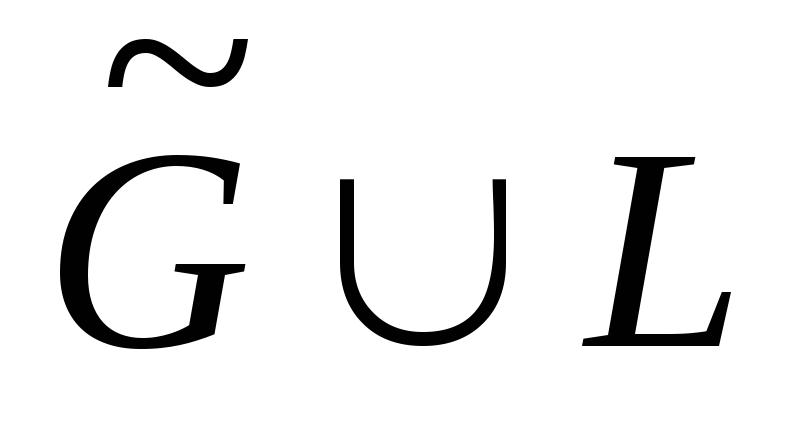 и перейдем к п.1
и перейдем к п.1 -
П
 остроена
укладка
остроена
укладка
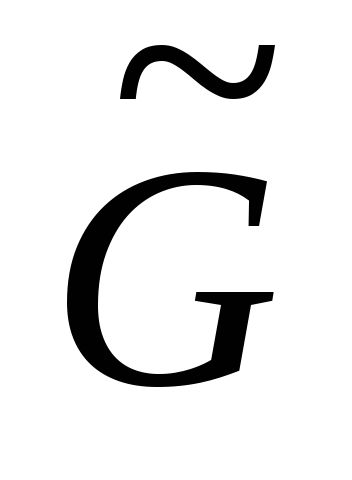 графа
графа
 на плоскости. Конец.
на плоскости. Конец.
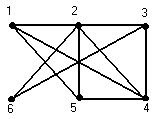
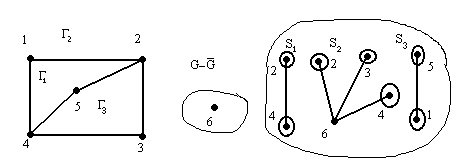
Уложим сначала цикл
![]() ,
который разбивает плоскость на две
грани
,
который разбивает плоскость на две
грани
![]() и
и
![]() .
.
![]()
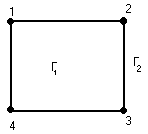
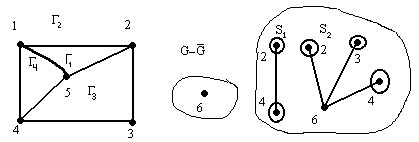
Найдем его сегменты.
![]()
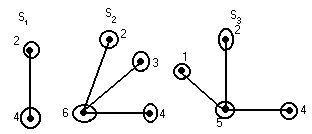
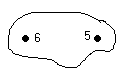
![]() - контактные вершины.
- контактные вершины.
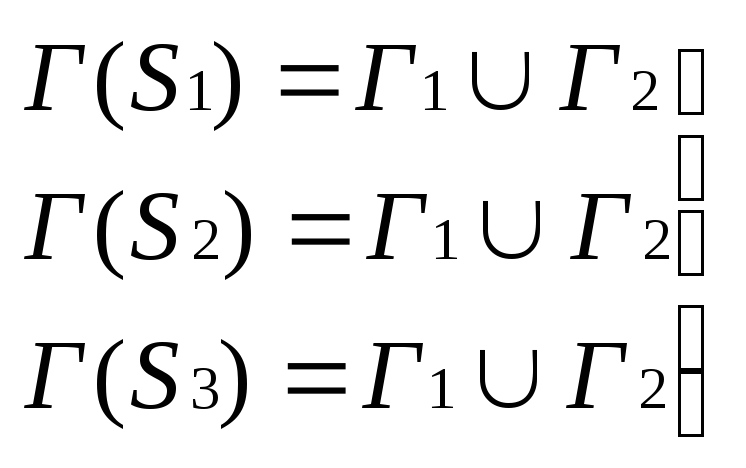 -допустимые грани
-допустимые грани
![]()
![]()


EMBED
Equation.3
![]()
![]()
![]()
![]()
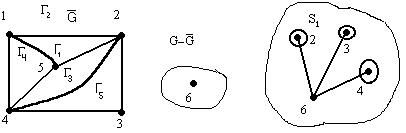
![]()
![]()
![]()

![]()
![]()