3. Двойственная задача в лп.

Каждой задаче ЛП можно поставить в соответствие другую задачу ЛП, называемую двойственной.

Рассмотрим две задачи:

1: найти (1.13)

при этом

(1.14)

2: найти (1.15)

при этом

(1.16)

Задача (2) называется двойственной задаче (1), при этом задача (1) называется прямой задачей ЛП.

Пример1.7:

Найти max f(x) = 4x₁ + 5x₂ + 9x₃

min φ(y) =16y₁ + 25y₂

Пример 1.8:

Найти max f(x) = x₁ - 4x₂ - 3x₃

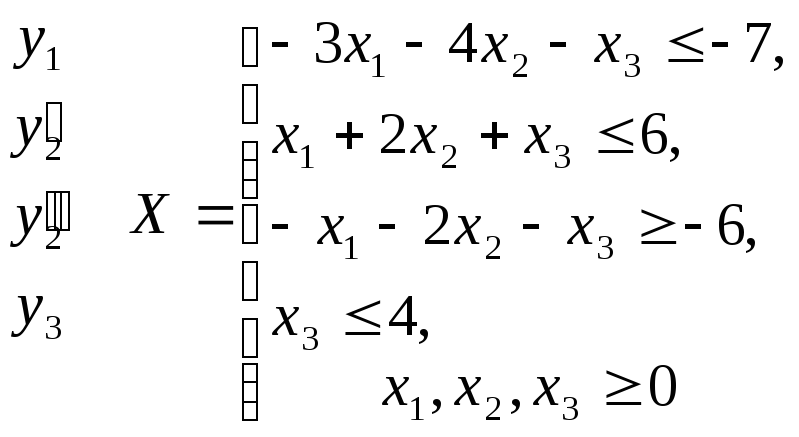
Запишем двойственную задачу:

min φ(y)= -7y₁ + 6y'₂ - 6y''₂ + 4y₃

Конечная форма двойственной задачи:

y₂ = y'₂ - y''₂

min φ(y) = -7y₁ + 6y₂ + 4y₃

Пример 1.9:

найти max f(x) = -6x₁ - 10x₂

найти max f(x) = -6x₁ - 10

Запишем двойственную задачу:

найти min φ(y) = -10y₁ + 4y₂

1.3.1 Правила и особенности перехода к двойственной задаче.

1. Столбцы коэффициентов ограничений прямой задачи совпадают со строками коэффициентов ограничений двойственной задачи.

2. Строка коэффициентов целевой функции прямой задачи совпадает со столбцом правых частей ограничений двойственной задачи.

3. Столбец правых частей ограничений прямой задачи совпадает со строкой коэффициентов целевой функции двойственной задачи.

4. Направление знаков неравенств коэффициентов прямой задачи противоположно направлению знаков неравенств двойственной задачи.

5. Если ограничение в прямой задаче задано в виде равенства, то соответствующая переменная двойственной задачи будет неопределенного знака.

6. Если переменная прямой задачи неопределенного знака, то соответствующее ограничение двойственной задачи будет со знаком равенства.

7. Требование максимизации в прямой задаче заменяется минимизацией в двойственной задаче.

8. Число ограничений в прямой задаче совпадает с числом переменных в двойственной задаче.

9. Число переменных в прямой задаче совпадает с числом ограничений в двойственной задаче.

1.3.2. Теоремы двойственности.

Теорема 1: Для любых допустимых планов и для исходной и двойственной задач значение целевой функции в задаче максимизации не больше значения целевой функции в задаче минимизации.

(1.17)

Экономический смысл: суммарный доход от реализации продукции не больше суммарной оценки ресурсов.

Теорема 2: Если исходная и двойственная ей задачи имеют допустимый план, то существует оптимальный план исходной задачи идвойственной задачи.

Теорема 3 (первая основная теорема двойственности): Если одна из задач двойственной пары имеет оптимальный план, то другая – также имеет оптимальный план.

Для любых оптимальных планов и имеет место равенство:

(1.18)

Теорема 4: (вторая основная теорема двойственности – теорема о дополнительной нежесткости): Для того чтобы допустимые планы ипары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:

(1.19)

Это означает, что если какое-либо ограничение одной задачи при подстановке в него оптимального плана обращается в строгое неравенство, то соответствующая этому ограничению переменная в оптимальном плане двойственной задачи равна 0.

Если какая-либо переменная в оптимальном плане одной задачи положительна, то соответствующее ей ограничение двойственной задачи при подстановке в него оптимального плана обращается в равенство.

Если (1.20)

Если (1.21)

Если (1.22)

Если (1.23)

Пример 1.10:

Используя теоремы двойственности найти решение ЗЛП

max f(x) = 7x₁ + x₃ - 4x₄

Решение:

min φ(y) = 6y₁ - y₂

Надо найти х.

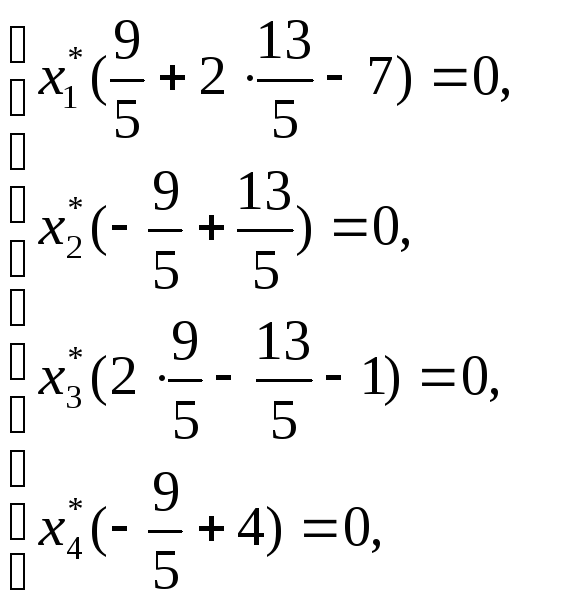
Найдем и :

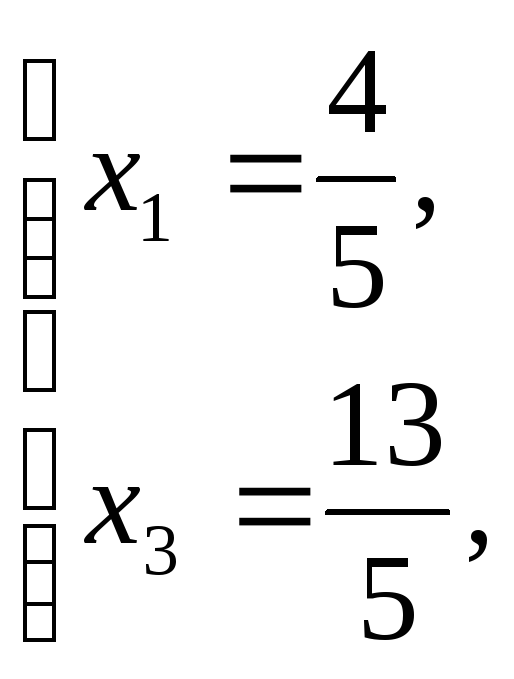
Значения совпали.

Пример 1.11:

Найденное оптимальное решение (см. предыдущую тему):

Запишем двойственную задачу

.