-
Редукция и конверсия -термов.
Определим
преобразование термов (известное и в
других формальных системах с переменными
и операторами) и назовем его
-правилом,
или правилом замены операторной
(связанной) переменной:
Так
как
,
то и, обратно,
.
В связи с этим, это правило называют
правилом
-конверсии
термов. Далее термы рассматриваются с
точностью до
-конверсии
или, иными словами, с точностью до
обозначения связанных переменных. С
учетом этого замечания можно доопределить
и операцию подстановки. В ранее не
определенном случае всегда можно найти
переменную
,
такую, что
,
и сделав замену переменной
на
,
можно внести операцию подстановки под
знак
-оператора:
.
Основу
-исчисления
составляет так называемое правило
-редукции
термов, формализующее связь аппликации
и
-оператора.
Если вспомнить, что неформальной основой
-исчисления
является
-нотация
функций, то легко заметить, что значение
функции
для аргумента, являющегося значением
выражения
,
есть значение выражения, полученного
подстановкой
в выражение
вместо переменной
,
точнее, вместо ее свободных вхождений
в выражение
.
Так, например, значение функции
для аргумента – денотата константы 3,
есть денотат константы
,
то есть число десять. Формально эта
взаимосвязь представлена в
-исчислении
в форме бинарного отношения
так называемой
-редукции
термов, определяемого как некоторое
замыкание базового отношения
между термами:
.
Терм
слева называется
-редексом,
а справа -
-контрактом.
Отношение
-редукции
определяется как наименьшее отношение,
удовлетворяющее следующим требованиям:
-
. -
. -
. -
,
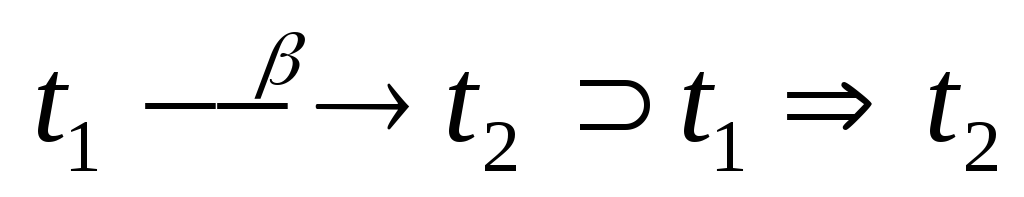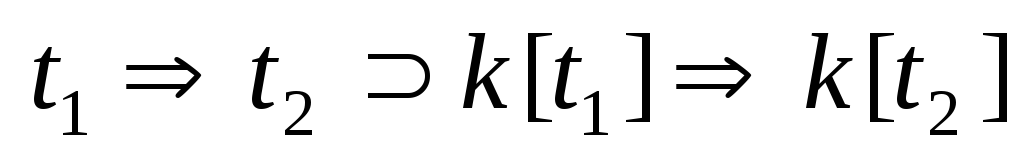где
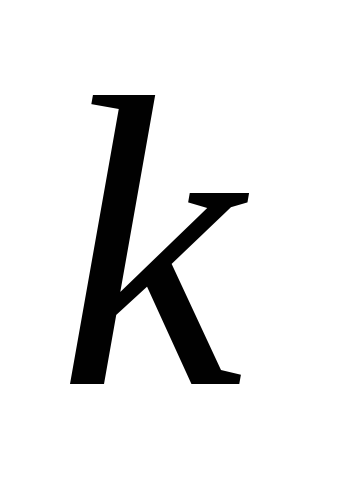- произвольный
-контекст.
Еще
раз заметим, что термы рассматриваются
с точностью до
-конверсии.
Последовательность
термов
,
,
называется процессом редукции терма
к терму
,
если
-
, -
, -
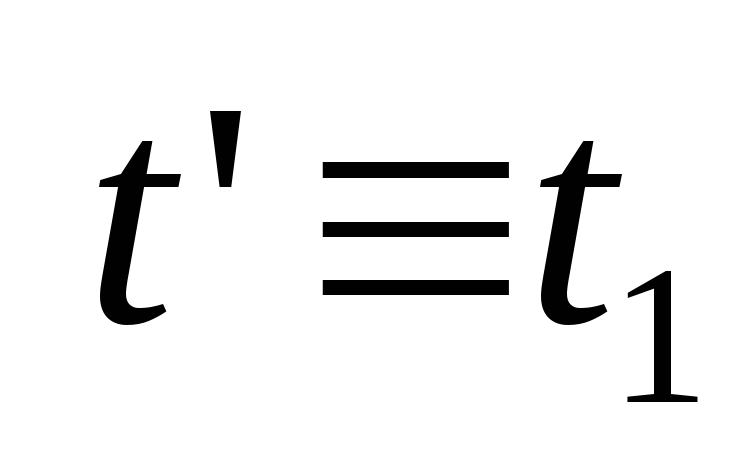для всех
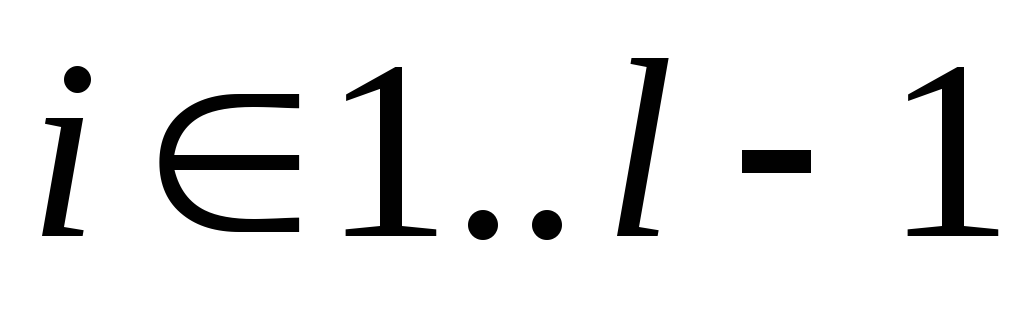существуют
-редекс
,
соответствующий ему
-контракт
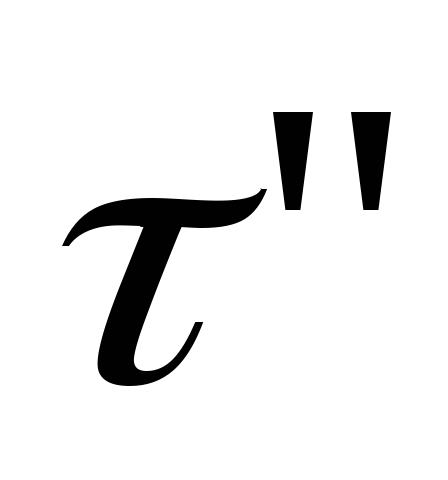и контекст
,
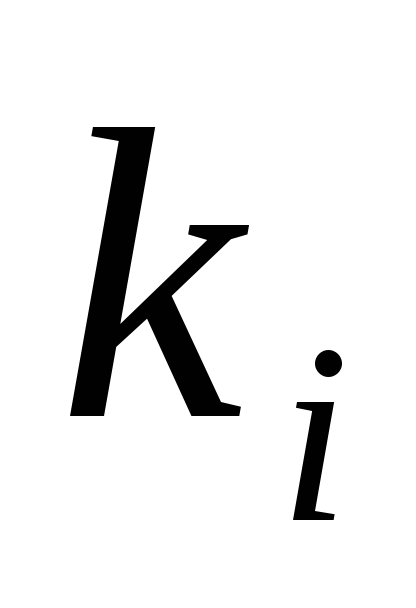такие, что
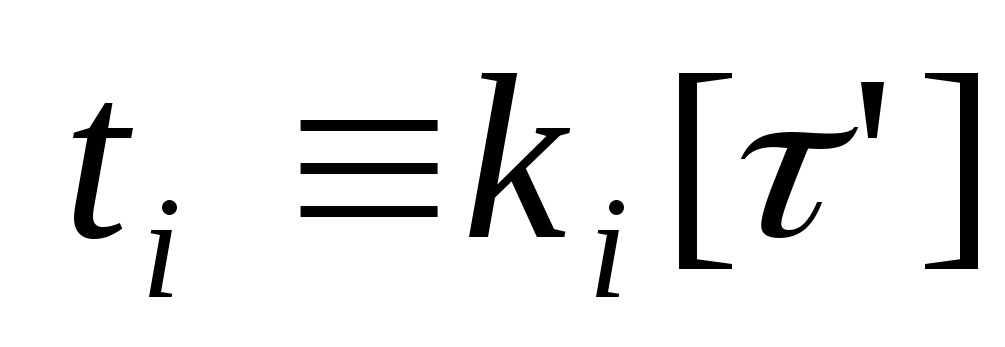и
.
Определение
1. Терм
находится в нормальной форме, если
он не содержит
-редексов.
Иными словами, терм
находится в нормальной форме, если не
существуют такие
и контекст
,
что
.
Очевидно,
что соответствующий предикат
,
проверяющий, находится терм – аргумент
в нормальной форме или нет, рекурсивен
(разрешим). В следующем разделе можно
найти его описание.
Определение
2. Терм
имеет нормальную форму, если
существует такой терм
в нормальной форме, что
.
Нетрудно
привести примеры термов, как имеющих,
так и не имеющих нормальную форму: термы
,
находятся в нормальной форме и,
следовательно, имеют нормальную форму,
терм
не находится в нормальной форме, но
имеет нормальную форму
,
а терм
не имеет нормальной формы (представляет
собой
-редекс,
после замены его на контракт вновь
представляет собой тот же самый
-редекс
и т.д.).
Определение
3. Процесс редукции
,
,
называется стандартной редукцией,
если на каждом шаге
в качестве контекста
вхождения заменяемого на контракт
-редекса
выбирается контекст самого левого из
всех вхождений любых редексов в терм
(
).
Заметим, что все вхождения
-редексов
в некоторый терм естественно упорядочиваются
слева направо по позициям, занимаемым
в терме внешними открывающими скобками
вхождений этих редексов).
Теорема 1 (о стандартной редукции).
Если терм имеет нормальную форму, то она достигается в результате стандартной редукции.
Доказательство. Кратко, идея доказательства такова. Нетрудно показать, что самый внешний редекс терма остается редексом в результате замены любых других редексов на соответствующие контракты. Поэтому для получения в результате редукции терма в нормальной форме замена его на контракт необходима. В то же время в результате этой замены некоторые из других редексов могут исчезнуть, не оставив «потомков».
Стандартная
редукция
-термов
в программировании является аналогом
стратегии вызова параметров функций
по имени (или стратегии так называемых
ленивых вычислений), как альтернативы
стратегии вызова параметров по значению
(энергичных вычислений) Как известно,
стратегия вызова параметров функций
по имени позволяет достигнуть максимально
возможной результативности вычисления
значения функции (для параметров процедур
с «побочным эффектом» эти стратегии, в
общем случае, могут приводить к разным
результатам).
Определение
4. Отношение редукции на некотором
множестве
термов называется конфлюэнтным,
если имеет место утверждение:
.
Теорема 2 (Черча-Россера).
Отношение
-редукции
на множестве
-термов
является конфлюэнтным.
Доказательство
можно найти в монографиях, посвященных
более глубокому изложению теории
-исчисления,
например в [2].
Следствие 1 (теоремы 2).
Если
-терм
имеет нормальную форму, то она –
единственная (с точностью до
-конверсии).
Доказательство очевидно.
Если
к определению отношения
-редукции
термов добавить дополнительно условие
симметричности, то минимальное отношение,
удовлетворяющее перечисленным ниже
требованиям, называется отношением
-конверсии
термов и обозначается инфиксом
:
-
. -
. -
. -
. -
,
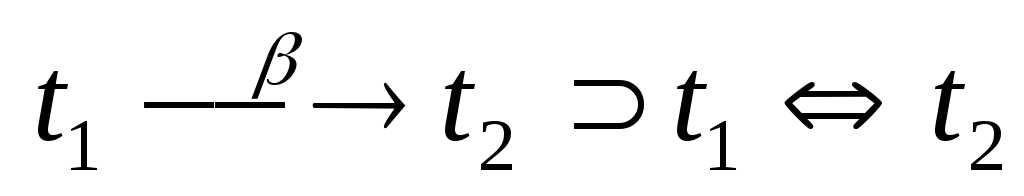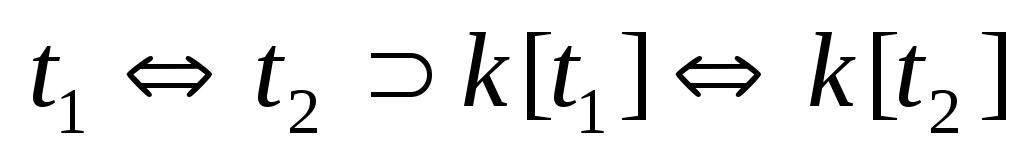где
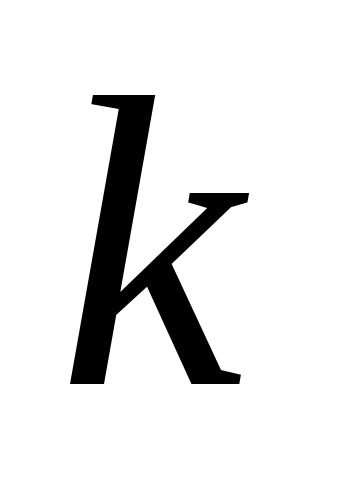- произвольный
-контекст.
Следствие 2 (теоремы 2).
Если
(терм
конвертируется с термом
),
то существует такой терм
,
что
и
.
Доказательство очевидно.
Соглашение об обозначениях.
Для
облегчения дальнейшего изложения примем
некоторые соглашения о сокращенном
представлении
-термов:
-
-
-
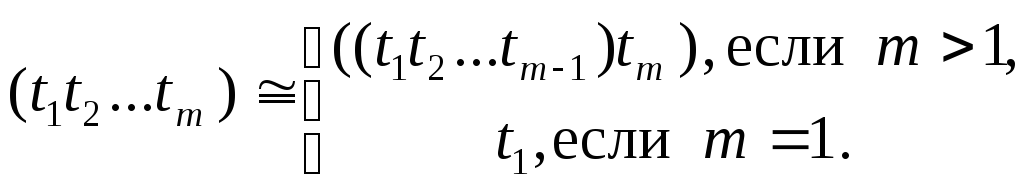
Внешние скобки в представлении
-термов,
полученных аппликацией, внутри текстов
могут быть опущены (в основном, этим
соглашением мы будем пользоваться при
формулировке одного из вариантов
комбинаторного исчисления в разделе
5). -
Вместо символов переменных
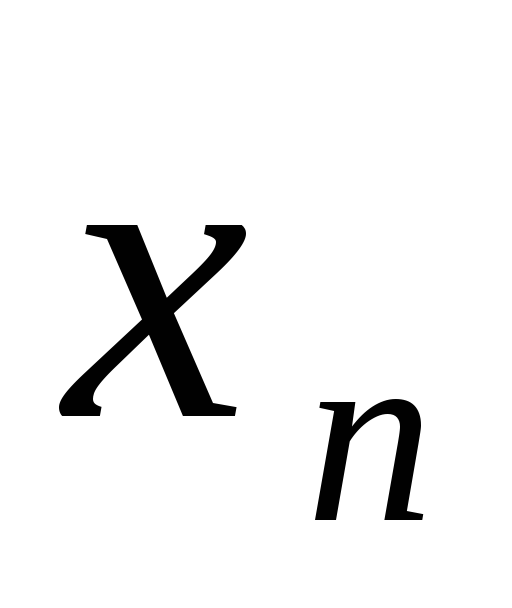могут использоваться любые строчные
латинские буквы, причем разным буквам
будут соответствовать переменные с
разными номерами. -
Прописные латинские буквы в позициях переменных рассматриваются как метапеременные; в качестве их значений могут быть переменные с любыми конкретными номерами.
Например,
запись
представляет собой сокращенную запись
терма
.
Теорема 3 (Карри).
Для
любого
-терма
и любой переменной
существует
-терм
,
такой, что
.
Иными
словами, всякое уравнение
имеет решение в
-исчислении
(с точностью до отношения конверсии
термов).
Доказательство.
Пусть
(
называют парадоксальным комбинатором
Карри). Тогда терм
,
существование которого утверждает
теорема 3, может быть получен так:
.
Действительно,
-
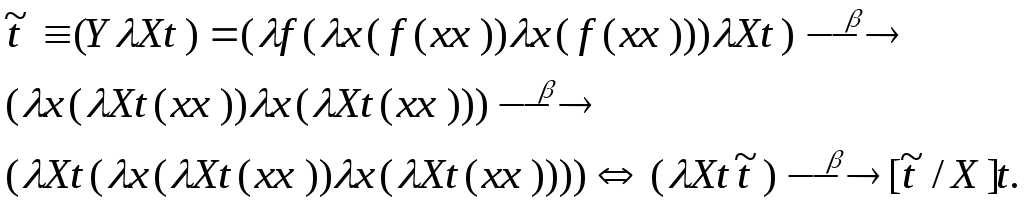
Моделирование в
-исчислении
конструктивных объектов и вычислимых
функций.
Пусть
- подмножество замкнутых, т.е. не содержащих
свободных вхождений переменных,
-термов
(
-термов);
- подмножество
-термов
в нормальной форме (
-термов),
а
- их пересечение (множество
-термов).
Пусть
- многосортный эрбрановский универсум,
где
- множество сортов объектов универсума.
Предположим, что для построения объектов
сорта
используется
различных конструкторов:
,
где
- арность
-го
конструктора для сорта
.
Для всех
через
обозначим взаимно-однозначные отображения
в множество
-термов.
Если
,
то
будем далее обозначать как «
»
и называть
-образом
объекта
.
Если для построения объектов различных
сортов используются различные наборы
конструкторов, то в обозначении
-образа
объекта
нет необходимости указывать его сорт
,
и он обозначается просто как «
».
Определим образы объектов по общему
правилу. Пусть
.
Тогда «
»
«
»«
»…«
»
.
-образом
функции
,
вообще говоря, частичной, назовем такой
-терм
«
»,
что для всех наборов значений аргументов
из области определения функции
(
,
,…,
или имеет место
«
»«
»«
»…«
»
«
»,
или
«
»«
»«
»…«
»
не имеет нормальной формы, если значение
не определено. Возможность решения
уравнений в
-исчислении
с помощью комбинатора Карри позволяет
пользоваться рекурсивной формулировкой
образов моделируемых функций. Конструкция
же образа «
»
любого объекта
такова, что терм вида
«
»
фактически осуществляет разбор случаев
конструкции объекта
,
так как
«
»
«
»«
»…«
»
,
если
.
Следовательно, терм
должен определять необходимое значение
для этого случая как функцию от образов
тех объектов, из которых построен объект
с помощью
-го
из конструкторов для объектов сорта
.
Для
освоения техники описанного моделирования
в
-исчислении
различных конструктивных объектов и
функций на этих объектах, в том числе и
предикатов, познакомимся с некоторыми
примерами. Будем, как и ранее, использовать
имена, начинающиеся со строчных букв
для обозначения сортов объектов, а
имена, начинающиеся с прописных букв,
для обозначения конструкторов. В случае,
когда конструируемые объекты имеют
общепризнанное представление, будем
на его основе определять вводимые
конструкторы. Арность конструкторов
при необходимости указывается в скобках
в качестве верхнего индекса.
Пример
1. Сорт
- логические значения, конструкторы
,
:
«
»
,
«
»
.
Заметим,
что образы логических значений играют
роль функций выбора значения одного из
двух аргументов, «
»
- первого, а «
»
- второго, что позволяет использовать
это при моделировании условных определений
.
Действительно,
«
»
,
а
«
»
.
Пример
2. Сорт
- натуральные числа, конструкторы
,
:
«
»
,
«
»
«
»
.
«
»
«
»
.
В этом рекурсивном описании образа
функции сложения натуральных чисел
предполагается, что вместо переменной
будет подставлен образ числа, на единицу
меньшего числа, образ которого
подставляется вместо переменной
.
Явное решение этого уравнения может
быть получено так:
«
»
«
»
«
»
«
»
«
»
.
«
»
«
»
.
В этом примере используется упомянутый
выше прием условного определения.
«
»
«
»
«
»
.
Описание образа функции умножения
натуральных чисел.
«
»
«
»
«
»
«
»
.
Описание образа функции возведения в
степень для натуральных чисел.
«
»
«
»
«
»
«
»
.
Описание образа функции вычисления
номера упорядоченной пары натуральных
чисел диагональным способом нумерации.
Пример
3. Сорт
- последовательности натуральных чисел
любой конечной длины, конструкторы
,
,
где
:
«
»
,
«
»
«
»«
»
.
«
»
«
»
.
Описание образа функции сцепления двух
последовательностей в одну.
«
»
«
»
.
Описание образа функции включения числа в качестве последнего элемента в заданный список.
«
»
«
»
«
»
.
Описание образа функции, изменяющей
порядок следования элементов
последовательности на обратный.
«
»
«
»
«
»
«
»
.
слияния двух упорядоченных по
неубыванию последовательностей
натуральных чисел в одну общую неубывающую
последовательность.
«
»
«
»
.
Описание функции, выделяющей подсписок
элементов с нечетными номерами в списке
– аргументе.
«
»
«
»
.
Описание функции, выделяющей подсписок
элементов с четными номерами в списке
– аргументе.
«
»
«
»
«
»
«
»
«
»
«
»
.
Описание функции сортировки по неубыванию
последовательности натуральных чисел
методом слияния.
Пример
4. Сорт
-
-термы,
конструкторы
,
и
:
«
»
«
»
,
«
»
«
»«
»
,
«
»
«
»«
»
,
«
»
«
»
«
»
«
»
«
»
«
»
.
Описание предиката, устанавливающего,
находится
-терм
в нормальной форме или нет.
- вспомогательный предикат:
«
»
«
»
«
»
«
»
«
»
«
»
.
«
»
«
»
«
»
«
»
«
»
«
»
«
»
«
»
.
Описание предиката
,
где
«
»
«
»
«
»
«
»
«
»
.
Описание предиката неравенства двух
натуральных чисел.
«
»
«
»«
»
.
Описание функции, вычисляющей наименьший
номер переменной, не имеющей свободных
вхождений в заданный терм, с помощью
вспомогательной функции «
»:
«
»
«
»
«
»
.
«
»
«
»
«
»
«
»
«
»
«
»
«
»
«
»
.
Описание функции, вычисляющей результат
подстановки одного терма вместо свободных
вхождений переменной с заданным номером
в другой терм.
«
»
«
»
«
»
«
»
.
Описание частичной функции, вычисляющей
нормальную форму заданного
-терма.
«
»
«
»
«
»
«
»
«
»
«
»
«
»
.
Описание функции, вычисляющей шаг
редукции для самого левого редекса
заданного
-терма,
не находящегося в нормальной форме.
«
»
,
т. е.
«
»«
»«
»
«
».
«
»
- образ функции, вычисляющей образ
заданного терма, т.е.
«
»«
»
««
»».