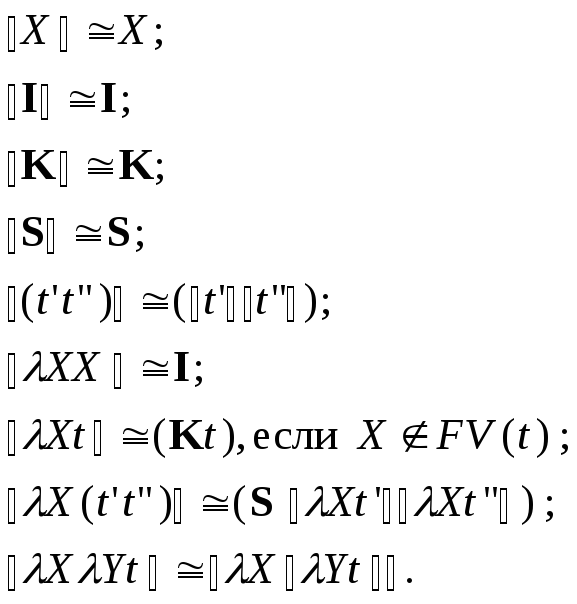4. Алгоритмически неразрешимые проблемы.

Теорема 4(о существовании специальной фиксированной точки).

Для всякого -терма существует -терм , такой, что «».

Доказательство.

Пусть «», где «»«». Действительно,

«»«»«»«»«»«»«»

«»«»««»»««»»«».

Определение 5. Пусть и - подмножества множества . называется рекурсивно отделимым от , если существует рекурсивное подмножество множества , такое, что и .

Напомним, что подмножество множества называется рекурсивным, если существует всюду определенный на вычислимый предикат , такой, что .

Определение 6. Подмножество множества называется нетривиальным, если и .

Определение 7. Подмножество -термов замкнуто относительно отношения -конверсии, если .

Теорема 5 (о рекурсивной неотделимости).

Два произвольных нетривиальных подмножества -термов, замкнутых относительно отношения -конверсии, не являются рекурсивно отделимыми.

Доказательство.

Пусть и - два подмножества -термов, удовлетворяющие условиям теоремы. Так как они не пересекаются (в этом случае результат очевиден) и не пусты, то выберем в них по одному элементу: и . Предположим от противного, что существует рекурсивное подмножество , такое, что и . Рекурсивность означает, что существует всюду определенный на множестве -термов вычислимый предикат , такой, что 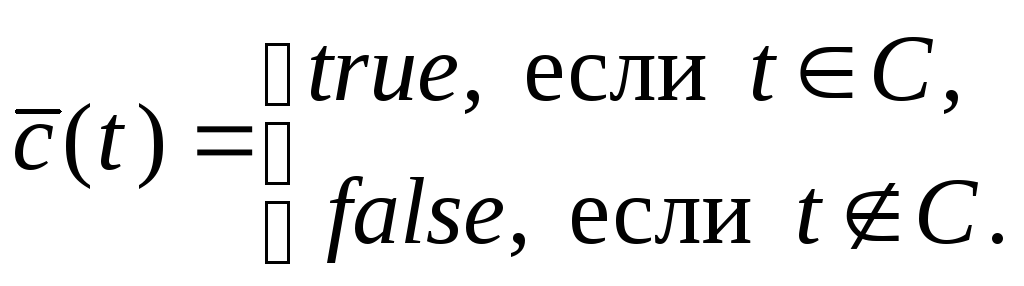Вычислимость этого предиката означает, что существует его -образ «», такой, что «»«»«», если , и «»«»«», если .

Построим терм «», для которого будет иметь место утверждение: если , то «», если , то «». Согласно теореме 4 построим для -терма такой -терм , что «». Возникает вопрос: или ? Начнем с первого предположения. Так как и , то . С другой стороны, «», и, в силу замкнутости относительно отношения -конверсии, . Получилось противоречие. Рассмотрим второе предположение. Так как , а , то . С другой стороны, «», и, в силу замкнутости относительно отношения -конверсии, . Вновь получилось противоречие. Следовательно, исходное предположение о рекурсивной отделимости и ложно.

Следствие 1 (теоремы 5).

Множество -термов, имеющих нормальную форму, не рекурсивно.

Доказательство. Достаточно рассмотреть множество -термов, имеющих нормальную форму, и его дополнение до множества всех -термов. Пара этих множеств удовлетворяет условиям теоремы 5. Если бы множество было бы рекурсивно, то это противоречило бы утверждению теоремы (в качестве множества можно было бы взять само ).

Аналогичным образом можно получить и другие результаты. Например,

Следствие 2 (теоремы 5).

Множество -термов, находящихся с заданным термом в отношении -конверсии, не рекурсивно.

Следствие 3 (теоремы 5).

Любое нетривиальное подмножество -термов, замкнутое относительно отношения -конверсии, не рекурсивно.

И так далее…

Доказательства аналогичны доказательству следствия 1.

5. Комбинаторное исчисление.

При более внимательном рассмотрении -исчисления, прежде всего, правила -редукции, возникает мысль о реализации идей декомпозиции -термов и построения формальной системы, обладающей теми же возможностями как математической модели вычислимости, что и -исчисление, но без явного введения на синтаксическом уровне -оператора, а вследствие этого, и без использования понятия связанной переменной, -конверсии и т.д.

Введем три «комбинатора» – три замкнутых, т.е. не содержащих свободных вхождений переменных, -терма в нормальной форме:

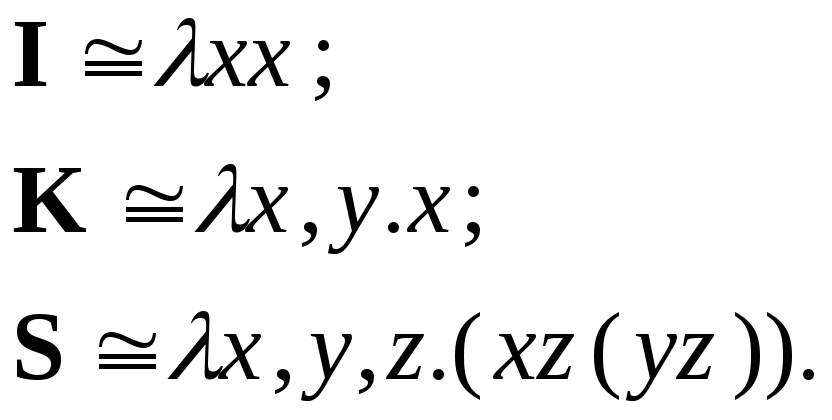
Определим специальное представление -термов, как будет показано далее, экстенсионально эквивалентное: