Национальный Исследовательский Университет

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

Институт автоматики и вычислительной техники

Кафедра прикладной математики

Лабораторная работа № 2

Решение задачи поиска кратчайшего пути в обыкновенном графе с учетом веса рёбер

Курс «Параллельные системы и параллельные вычисления»

Выполнил

студент 5 курса группы А-13-08

Захаров Антон

Преподаватель

Панков Николай Александрович

Постановка задачи

Пусть дана матрица смежности графа :

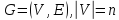Требуется найти путь минимальной длины из начальной вершины в конечную .

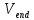Для нахождения кратчайшего пути необходимо составить последовательно-параллельную программу на языке C/C++ с применением интерфейса передачи сообщений (MPI, Message Passing Interface), а также исследовать характеристики разработанной программы в зависимости от числа исполнителей.

Последовательный алгоритм решения Алгоритм Флойда-Уоршелла

Один из нескольких алгоритмов, высчитывающих кратчайшие расстояния между всеми вершинами взвешенного ориентированного графа на ряду с алгоритмами Дейкстры, Джонсона и Данцига.

Пусть вершины графа 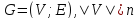пронумерованы от 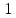до 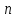и введено обозначение 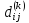для длины кратчайшего пути от 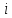до 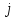, который кроме самих вершин 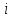, 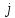проходит только через вершины . Очевидно, что 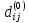– длина (вес) ребра 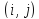, если таковое существует (в противном случае его длина может быть обозначена как ).

Существует два варианта значения :

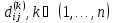1. Кратчайший путь между 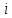, 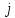не проходит через вершину , тогда

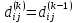
2. Существует более короткий путь между i,\;j, проходящий через k, тогда он сначала идёт от 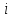до 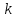, а потом от 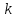до 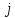. В этом случае, очевидно,

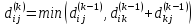
Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений.

Алгоритм Флойда-Уоршелла последовательно вычисляет все значен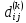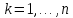ия , . Полученные значения 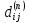являются длинами кратчайших путей между вершинами 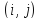. Алгоритм можно легко дополнить для получения интересующего пути, добавив вычисление матрицы предшествования .

1. for (k = 0; k < n; k++) {

2. for (i = 0; i < n; i++) {

3. for (j = 0; j < n; j++) {

4. if(M[i][j] > M[i][k] + M[k][j]) {

5. P[i][j] = P[k][j];

6. M[i][j] = M[i][k] + M[k][j];

7. } } } }

Параллельный алгоритм решения

В данной работе предложена параллельная реализация алгоритма Флойда-Уоршелла: матрица смежности и исходная матрица предшествования рассылаются на все узлы, каждый узел вычисляет по одной полосе фиксированного размера двух искомых матриц (матрицы весок кратчайших путей и матрицы предшествования). На каждой k-ой итерации происходит объединение результатов и повторная рассылка матриц узлам.

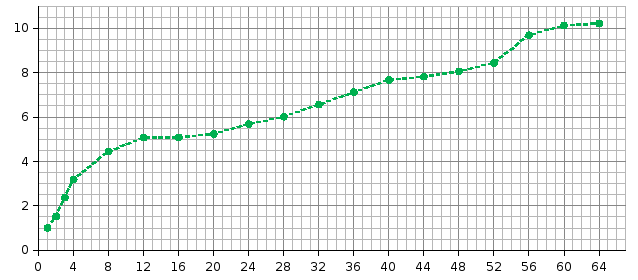
Результаты вычислительного эксперимента Число вершин 100

Число узлов	Число исполнителей на узле	Общее число исполнителей	Время решения^1 (сек)	Ускорение
1	1	1	0,14214	1,00000
1	2	2	0,09310	1,52670
1	3	3	0,05993	2,37179
1	4	4	0,04455	3,19037
2	4	8	0,03193	4,45093
3	4	12	0,02803	5,07051
4	4	16	0,02795	5,08462
5	4	20	0,02715	5,23588
6	4	24	0,02502	5,68143
7	4	28	0,02364	6,01243
8	4	32	0,02168	6,55732
9	4	36	0,01996	7,12086
10	4	40	0,01854	7,66733
11	4	44	0,01818	7,81905
12	4	48	0,01765	8,05527
13	4	52	0,01685	8,43797
14	4	56	0,01468	9,68230
15	4	60	0,01404	10,12669
16	4	64	0,01392	10,21372

Время

(сек)

Зависимость времени решения задачи от числа исполнителей

Число

исполнителей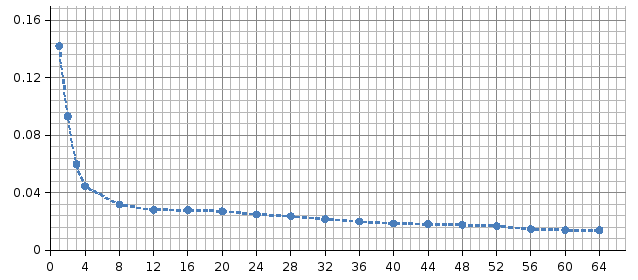

Ускорение

Зависимость ускорения параллельного решения от числа исполнителей

Число

исполнителей