
Задача 18.
Построить кривую, заданную уравнением, приведя его к каноническому виду. Определить:
-
для окружности – координаты центра и радиус;
-
для эллипса – координаты центра, полуоси, координаты фокусов, эксцентриситет, уравнения директрис;
-
для гиперболы – координаты центра, действительную и мнимую полуоси, координаты фокусов, эксцентриситет, уравнения директрис, уравнения асимптот;
-
для параболы – координаты вершины, параметр параболы, координаты фокуса, уравнение директрисы.
Решение.
а)
Исследуем кривую второго порядка,
заданную своим уравнением
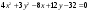 .
.
В этом уравнении второго порядка коэффициенты при квадратах переменных имеют одинаковый знак. Значит, уравнение относится к эллиптическому типу. Выделяя полные квадраты по обоим переменным, получаем
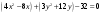 ,
,
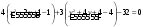 ,
,
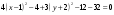 ,
,
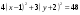 ,
,
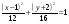 .
.
Точка
 центр эллипса.
центр эллипса.
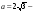 малая полуось,
малая полуось,
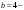 большая полуось эллипса. Так как
большая полуось эллипса. Так как
 ,
то фокусы лежат на вертикальной оси
симметрии. Поэтому
,
то фокусы лежат на вертикальной оси
симметрии. Поэтому
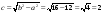 ,
а эксцентриситет (отношение фокального
расстояния эллипса к его большой оси)
,
а эксцентриситет (отношение фокального
расстояния эллипса к его большой оси)
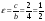 .
Координаты фокусов:
.
Координаты фокусов:
 .
Уравнения директрис:
.
Уравнения директрис:
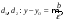 ;
для данного эллипса:
;
для данного эллипса:
 .
.
Рисунок
б)
В уравнении кривой второго порядка
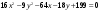 коэффициенты при квадратах переменных
имеют противоположный знак. Поэтому
уравнение относится к гиперболическому
типу. Выделяя полные квадраты по обоим
переменным, получаем
коэффициенты при квадратах переменных
имеют противоположный знак. Поэтому
уравнение относится к гиперболическому
типу. Выделяя полные квадраты по обоим
переменным, получаем
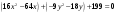 ,
,
 ,
,
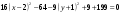 ,
,
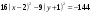 ,
,
 .
.
Уравнение
задает сопряженную гиперболу с центром
в точке
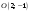 ,
действительной полуосью
,
действительной полуосью
 ,
мнимой полуосью
,
мнимой полуосью
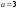 .
При этом
.
При этом
 ,
а эксцентриситет (отношение фокального
расстояния гиперболы к ее действительной
оси)
,
а эксцентриситет (отношение фокального
расстояния гиперболы к ее действительной
оси)
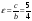 .
Координаты фокусов:
.
Координаты фокусов:
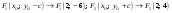 .
Уравнения директрис:
.
Уравнения директрис:
 ;
для данной гиперболы:
;
для данной гиперболы:
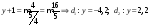 .
Уравнения асимптот:
.
Уравнения асимптот:
 ;
для данной гиперболы:
;
для данной гиперболы:

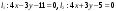 .
.
Рисунок
в)
Уравнение кривой второго порядка
 относится к параболическому типу,
поскольку содержит только одно слагаемое
с переменным в квадрате. Выделяя полный
квадрат по
относится к параболическому типу,
поскольку содержит только одно слагаемое
с переменным в квадрате. Выделяя полный
квадрат по
 ,
получаем
,
получаем
 ,
,
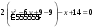 ,
,
 ,
,
 ,
,
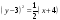 ,
,
 .
.
Это
парабола с горизонтальной осью симметрии,
для которой параметр
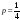 ,
а
,
а
 .
Вершина параболы находится в точке
.
Вершина параболы находится в точке
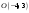 .
Координаты фокуса:
.
Координаты фокуса:
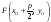 ;
для данной параболы
;
для данной параболы
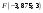 .
Уравнение директрисы
.
Уравнение директрисы
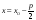 ;
для данной параболы
;
для данной параболы
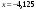 .
.
Рисунок
Задача 19.
Составить
уравнение плоскости, проходящей через
точку
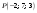 параллельно плоскости
параллельно плоскости
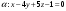 .
.
Решение.
В
качестве нормального вектора искомой
плоскости можно взять нормальный вектор
данной плоскости, то есть
 .
Теперь, зная нормаль плоскости и точку
.
Теперь, зная нормаль плоскости и точку
 ,
ей принадлежащую, запишем ее уравнение:
,
ей принадлежащую, запишем ее уравнение:
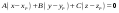 ,
,
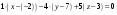 ,
,
 ,
,
 .
.
Задача 20.
Составить
уравнение плоскости, проходящей через
точку
 перпендикулярно к вектору
перпендикулярно к вектору
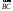 ,
если
,
если
 .
.
Решение.
Найдем
вектор
 :
:
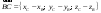 ,
,
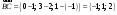 .
.
Так как он перпендикулярен к плоскости, то, используя его в качестве нормального вектора, запишем уравнение плоскости:
 ,
,
 ,
,
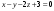 .
.
Задача 21.
Найти
расстояние от точки
 до плоскости
до плоскости
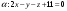 .
.
Решение.
Расстояние от точки до плоскости находим по формуле:
 ,
,
где
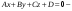 уравнение плоскости.
уравнение плоскости.
Имеем
 .
.
Задача 22.
Найти
угол между плоскостями
 .
.
Решение.
Угол
 между плоскостями определяется как
угол между их нормальными векторами.
Нормальные векторы данных плоскостей
соответственно равны
между плоскостями определяется как
угол между их нормальными векторами.
Нормальные векторы данных плоскостей
соответственно равны
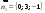 и
и
 .
По формуле найдем косинус искомого угла
.
По формуле найдем косинус искомого угла
 :
:
 ,
,
 ,
,
откуда
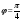 .
.
Задача 23.
Записать
канонические уравнения прямой, проходящей
через точки
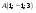 и
и
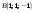 .
Выясните, лежит ли точка
.
Выясните, лежит ли точка
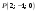 на этой прямой.
на этой прямой.
Решение.
Учитывая
уравнения прямой, проходящей через две
точки, уравнения прямой
 можно записать в виде:
можно записать в виде:
 ,
,
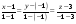 ,
,
 ,
,
и окончательно
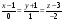 .
.
Чтобы
точка
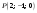 лежала на прямой
лежала на прямой
 ,
необходимо и достаточно, чтобы ее
координаты удовлетворяли уравнениям
данной прямой. Проверим это:
,
необходимо и достаточно, чтобы ее
координаты удовлетворяли уравнениям
данной прямой. Проверим это:
 ,
,
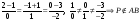 .
.
Задача 24.
Прямая задана общими уравнениями
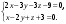
Записать ее канонические и параметрические уравнения.
Решение.
Для
записи канонических уравнений прямой
надо знать какую-нибудь точку этой
прямой и ее направляющий вектор. В
качестве координат точки прямой можно
взять любое решение данной системы двух
уравнений, например
 ,
а направляющий вектор найдем по формуле
,
а направляющий вектор найдем по формуле
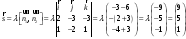 .
.
Тогда
 ,
,
 канонические
уравнения прямой.
канонические
уравнения прямой.
Каждое
отношение в последнем соотношении
обозначим буквой
 :
:
 ,
,
то
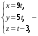 параметрические
уравнения прямой.
параметрические
уравнения прямой.
Задача 25.
Составить
канонические уравнения прямой, которая
проходит через точку
 перпендикулярно плоскости
перпендикулярно плоскости
 .
.
Решение.
Нормальный
вектор плоскости параллелен прямой и
его можно принять в качестве ее
направляющего вектора. Зная точку
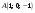 и направляющий вектор
и направляющий вектор
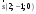 прямой, запишем ее канонические уравнения:
прямой, запишем ее канонические уравнения:
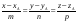 ,
,
 .
.
Задача 26.
Найти
точку пересечения прямой
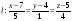 и плоскости
и плоскости
 .
Вычислить угол между прямой
.
Вычислить угол между прямой
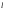 и плоскостью
и плоскостью
 .
.
Решение.
Точку пересечения прямой и плоскости можно найти из системы

где
 параметрические уравнения прямой
параметрические уравнения прямой
 ;
;
 уравнение плоскости
уравнение плоскости
 .
.
Канонические уравнения прямой перепишем в ее параметрические уравнения:
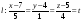 ;
;

Точка
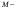 точка пересечения прямой
точка пересечения прямой
 и плоскости
и плоскости
 .
Ее координаты найдем из системы:
.
Ее координаты найдем из системы:
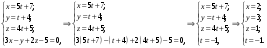
Следовательно,
 .
.
Зная
направляющий вектор
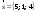 и нормаль
и нормаль
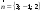 ,
вычислим по формуле величину
,
вычислим по формуле величину
 угла между данными прямой и плоскостью:
угла между данными прямой и плоскостью:
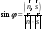 ,
,
 ,
,
 .
.
