17. Векторы на плоскости и в пространстве: определение, линейные операции

Вектор – это направленный отрезок прямой.

То есть, в качестве вектора мы принимаем отрезок на плоскости или в пространстве, считая одну из его граничных точек началом, другую – концом.

Для обозначения векторов будем использовать строчные латинские буквы со стрелочкой над ними, например . Если заданы граничные точки начала и конца отрезка, к примеру А и В, то вектор будем обозначать как .

Нулевой вектор  – это любая точка плоскости или пространства.

Будем считать, что нулевому вектору можно придать любое направление на плоскости и в пространстве.

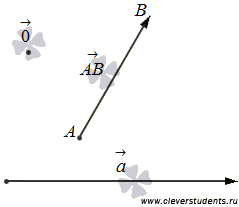
Длина вектора  - это неотрицательное число, равное длине отрезка АВ.

Длину вектора  будем обозначать как .

Так как обозначение длины вектора в точности совпадает со знаком модуля, то можно услышать, что длину вектора называют модулем вектора. Все же рекомендуем использовать термин "длина вектора". Длина нулевого вектора равна нулю.

Два вектора называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Два вектора называют неколлинеарными, если они не лежат на одной прямой или параллельных прямых.

Нулевой вектор коллинеарен любому другому вектору.

Два коллинеарных вектора  и  называют сонаправленными, если их направления совпадают и обозначают .

Два коллинеарных вектора  и  называют противоположно направленными, если их направления противоположны и обозначают ).

Будем считать, что нулевой вектор сонаправлен с любым другим вектором.

Два вектора называются равными, если они сонаправленные и их длины равны.

Два вектора называются противоположными, если они противоположно направлены и их длины равны.

Понятие равных векторов дает нам возможность рассматривать векторы без привязки к конкретным точкам. Другими словами, мы имеем возможность заменить вектор равным ему вектором, отложенным от любой точки.

Пусть  и  два произвольных вектора на плоскости или в пространстве. Отложим от некоторой точки O плоскости или пространства векторы  и . Лучи OA и OBобразуют угол .

Угол  называется углом между векторами  и .

Угол между сонаправленными векторами равен нулю градусам (или нулю радиан), а угол между противоположно направленными векторами равен 180 градусам (или  радиан).

Два вектора называются перпендикулярными, если угол между ними равен 90градусам

(или  радиан).

   Линейные операции над векторами.

 

Определение 5.4. Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

                   b

                         a+b

a

 

                                       Замечание. Такое правило сложения векторов называют правилом треугольника.

 

                             Свойства сложения:

Свойство 1. a + b = b + a.

Доказательство. Приложим векторы а и b к общему началу и рассмотрим параллелограмм

AOBC. Из определения 5.4 и треугольника ОВС следует, что ОС=b+a, а из треугольника

                                                 ОАС – ОС=а+b. Свойство 1 доказано.        

            В              а    С            Замечание. При этом сформулировано еще одно правило

          b                      b             сложения векторов – правило параллелограмма: сумма

                 a+b=                        векторов a и b есть диагональ параллелограмма, построенно-

                =b+a                         го на них как на сторонах, выходящая из их общего начала.           

 

О                   А

                 а

                                                                    Свойство 2. (a+b)+c=a+(b+c).

                                b                                 Доказательство. Из рисунка видно, что

          A                a+b      B                            (a+b)+c=(OA+AB)+BC=OB+BC=OC,

          a                                                             a+(b+c)=OA+(AB+BC)=OA+AC=OC.

                                                                         Свойство 2 доказано.

                       b+с

O                                       c  С

 

 

 

Свойство 3. Для любого вектора a существует нулевой вектор О такой, что a+О=а.

Доказательство этого свойства следует из определения 5.4.

 

Свойство 4. Для каждого вектора a существует противоположный ему вектор a^/ такой, что а+а^/=О.

Доказательство. Достаточно определить a^/  как вектор, коллинеарный вектору a, имеющий одинаковую с ним длину и противоположное направление.

 

Определение 5.5. Разностью а – b  векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

 

           a           a-b

 

 

                                           b

 

Определение 5.6. Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

 

Свойства умножения вектора на число:

Свойство 1. k(a + b) = ka + kb.

Свойство 2. (k + m)a = ka + ma.

Свойство 3. k(ma) = (km)a.

 

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.

18. Скалярное произведение векторов. Условия ортогональности двух векторов.

Скалярное произведение векторов.

 

Определение 5.14. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:

                         ab = |a||b| cosφ .                                                                         (5.4)

Обозначения скалярного произведения: ab, (ab), a·b .

 

 Свойства скалярного произведения:

 

1. ab = |a| пр_аb.

 

Доказательство. По свойству проекции пр_аb = |b| cosφ, следовательно, ab = |a| пр_аb.

 

2. ab = 0 a b.                                             3. ab = ba .

4. (ka)b = k(ab).                                                  5. (a + b)c = ac + bc .

6. a² = aa = |a|² , где а² называется скалярным квадратом вектора а.

7. Если векторы а и b определены своими декартовыми координатами

              a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂},                                               (5.5)

то            ab = X₁X₂ + Y₁Y₂ + Z₁Z₂ . 

                                                         (5.6)

Доказательство. Используя формулу (5.3), получим:

                          ab = (X₁i + Y₁j + Z₁k)(X₂i + Y₂j + Z₂k) .

 Используя свойства 4 и 5, раскроем скобки в правой части полученного равенства:

ab = X₁X₂ii +Y₁Y₂jj + Z₁Z₂kk + X₁Y₂ij +X₁Z₂ik + Y₁X₂ji + Y₁Z₂jk + Z₁X₂ki + Z₁Y₂kj.

Но ii = jj = kk = 1 по свойству 6, ij = ji = ik = ki = jk = kj = 0 по свойству 2, поэтому

                      ab = X₁X₂ + Y₁Y₂ + Z₁Z₂ . 

 

8. cosφ = .                                                  (5.6)

Замечание. Свойства 2, 3, 4 доказываются из определения 5.14, свойства 5, 6 – из свойств проекции, свойство 8 – из свойства 7 и свойств направляющих косинусов.

 

Пример.

a = {1, -5, 12}, b = {1, 5, 2}. Найдем скалярное произведение векторов а и b :

ab = 1·1 + (-5)·5 + 12·2 = 1 – 25 + 24 = 0. Следовательно, векторы а и b ортогональны.

 

Условия ортогональности векторов. Два вектора a и b ортогональны (перпендикулярны), если ихскалярное произведение равно нулю a · b = 0

19. координаты вектора: определения, действия с векторами, заданными своими координатами

Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

20. Общее уравнение прямой линии на плоскости

Теорема.

Всякое уравнение первой степени вида , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и любая прямая в прямоугольной системе координат Oxy на плоскости задается уравнением вида  при некотором наборе значений A, B и C.

Доказательство.

Как видите, теорема состоит из двух частей. Докажем сначала, что уравнение вида  задает прямую на плоскости.

Пусть координаты точки  удовлетворяют уравнению , то есть, . Вычтем из левой и правой частей уравнения соответственно левую и правую части равенства , при этом получаем уравнение вида , которое эквивалентно .

Уравнение  представляет собой необходимое и достаточное условие перпендикулярности двух векторов  и . То есть, множество всех точек  определяет в прямоугольной системе координат Oxy прямую линию, перпендикулярную направлению вектора . Если бы это было не так, то векторы  и  не были бы перпендикулярными и равенство  не выполнялось бы.

Таким образом, уравнение  задает прямую линию в прямоугольной декартовой системе координат Oxy на плоскости, следовательно, эквивалентное ему уравнение вида  задает эту же прямую. На этом первая часть теоремы доказана.

Теперь докажем, что всякая прямая в прямоугольной системе координат Oxy на плоскости определяется уравнением первой степени вида .

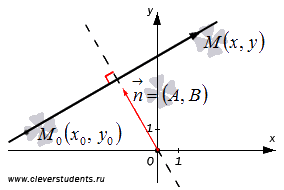
Пусть в прямоугольной системе координат Oxy на плоскости задана прямая a, проходящая через точку ,  - нормальный вектор прямой a, и пусть  - плавающая точка этой прямой. Тогда векторы  и  перпендикулярны, следовательно, их скалярное произведениеравно нулю, то есть, . Полученное равенство можно переписать в виде . Если принять , то получим уравнение , которое соответствует прямой a.

На этом доказательство теоремы завершено.

Уравнение вида  есть общее уравнение прямой на плоскости в прямоугольной системе координат Oxy.

Из доказанной теоремы следует, что в фиксированной прямоугольной декартовой системе координат Oxy на плоскости прямая линия и ее общее уравнение прямой неразделимы. Иными словами, заданной прямой соответствует ее общее уравнение прямой, а этому общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также видно, что коэффициенты А и В при переменных x и yявляются соответствующими координатами нормального вектора прямой, заданной общим уравнением прямой вида .

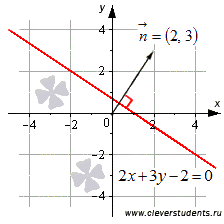
Приведем пример общего уравнения прямой.

Уравнению  соответствует прямая линия в заданной прямоугольной декартовой системе координат Oxy. Ее изображение представлено на чертеже. Нормальным вектором этой прямой линии является вектор .

С другой стороны, прямая линия, изображенная на рисунке, в прямоугольной системе координат Oxy задается общим уравнением прямой вида , так как координаты любой точки этой прямой удовлетворяют записанному уравнению.

Следует заметить, что уравнение вида , полученное из общего уравнения прямой умножением его обеих частей на отличное от нуля число , эквивалентно уравнению , следовательно, определяет ту же самую прямую на плоскости в фиксированной прямоугольной системе координат.