25 Унитарные и ортогональные матрицы.

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на AT равен единичной матрице:[1]

AAT = ATA = E,

или, что эквивалентно, её обратная матрица равна транспонированной матрице:

Унита́рная ма́трица — квадратная матрица с комплексными элементами, результат умножения которой на эрмитово сопряжённую равен единичной матрице:

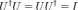
Другими словами, матрица унитарна тогда и только тогда, когда существует обратная к ней матрица, удовлетворяющая условию .

Унитарная матрица, элементы которой вещественны, является ортогональной.

Следующие утверждения относительно данной квадратной матрицы A являются эквивалентными:

A — унитарна.

унитарна.

Столбцы матрицы A образуют ортонормированный базис в унитарном пространстве.

Строки матрицы A образуют ортонормированный базис в унитарном пространстве.

27. Эллипс: определение, вывод канонического уравнения, исследование формы.

Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.

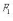
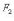
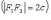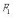
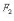Пусть на плоскости заданы две точки и дано число a (a > c). Эллипс - множество точек M плоскости, для каждой из которых сумма расстояний от точекравна 2a. Точкиназываются фокусами эллипса;- большая ось;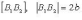- малая ось; O - центр;- левый и правый фокусы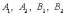- вершины;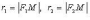- фокальные радиусы;

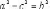
Каноническое уравнение:

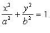
31 Поверхности второго порядка: канонические уравнения, исследование поверхности

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0

в котором по крайней мере один из коэффициентов a11, a22, a33, a12, a23, a13 отличен от нуля.

1) эллипсоиды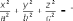

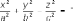
2) гиперболоиды: 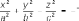3) параболоиды (p > 0, q > 0):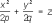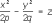4) конусы второго порядка:5) цилиндры второго порядка:При исследовании общего уравнения Поверхности второго порядка важное значение имеют т. н. основные инварианты — выражения, составленные из коэффициентов уравнения (*) и не меняющиеся при параллельном переносе и повороте системы координат. Например, еслито уравнение (*) определяет вырожденные Поверхности второго порядка: конусы и цилиндры второго порядка и распадающиеся Поверхности второго порядка; если определитель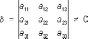то поверхность имеет единственный центр симметрии (центр Поверхности второго порядка) и называется центральной поверхностью. Если d = 0, то поверхность либо не имеет центра, либо имеет бесконечно много центров.

2) система линейных уравнений

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j– номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 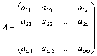, которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.

2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.

3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называетсянесовместной

Метод Гаусса — Жордана используется для решения систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе, отыскания ранга матрицы. Метод является модификацией метода Гаусса.

4)вычисление определителя

Минором M_ij элемента a_ij (i,j=1,n) называется определитель (n-1)-го порядка, полученный из определителя n-го порядка, вычерчиванием i-й строки и j-го столбца. Алгебраическое дополнение Aij элемента Aij определяется равенством 

A_ij=(-1)^i+j M_ij

Для произвольного натурального числа (теорема Лапласа, разложение по i-строке) 

свойства:

1. Если переставить две строки (или два столбца) определителя, то определитель изменит знак.

2. Если соответствующие элементы двух столбцов (или двух строк) определителя равны или пропорциональны, то определитель равен нулю.

3. Значение определителя не изменится, если поменять местами строки и столбцы, сохранив их порядок.

4. Если все элементы какой-либо строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Значение определителя не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число. Для определителей третьего порядка это свойство может быть записано, например, так:

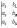
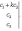
6. Определитель второго порядка вычисляется по формуле

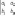
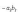(1)

7. Определитель третьего порядка вычисляется по формуле

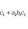
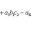
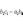
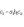(2)

Существует удобная схема для вычисления определителя третьего порядка (см. рис. 1 и рис. 2).

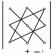
По схеме, приведенной на рис. 1, произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 - с обратным. Величина определителя равна алгебраической сумме полученных шести произведений.

6) Определение

Однородной (хо-мо-JEEN-я-нам) системы линейных алгебраических уравнений является одним

, в котором все цифры на правой стороне равны 0:

Однородной системы Ax = 0 всегда имеет решение х = 0.

Отсюда следует, что любая однородная система уравнений всегда последовательным. Любой ненулевой

решения, если они существуют, называются нетривиальных решений. Они могут или не могут существовать. Мы

можете узнать по строке сокращение соответствующих расширенной матрицы

 Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rankA < n.

     Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

     Тогда n - r линейно независимыми вектор-решениями будут:

а любое другое решение является их линейной комбинацией. Вектор-решения образуют нормированную фундаментальную систему.

В линейном пространстве 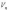множество решений однородной системы линейных уравнений образует подпространство размерности n - r; - базис этого подпространства.

8) обратная матрица