NAShI_OTVETY

1. Скорость и ускорение материальной точки.

Для характеристики движения материальной точки вводят векторную физическую величину - скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.

Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчѐта.

Скалярная величина, точнее модуль производной радиус-вектора.

Ускорение материальной точки прямо пропорционально действующей на нее силе и направлено по линии ее действия

2. Криволинейное движение. Угловая скорость. Угловое ускорение. Их связь с линейной скоростью и с линейным ускорением.

Пройденный путь S , перемещение dr, скорость v , тангенциальное и нормальное ускорение at, и an, представляют собой линейные величины. Для описания криволинейного движения наряду с ними можно пользоваться угловыми величинами.

называют угловой скоростью. Угловая скорость представляет собой вектор, направление которого связывают с направлением оси вращения тела (рис.).

Обратим внимание на то, что, в то время как сам угол поворота φ является скаляром, бесконечно малый поворот dφ — векторная величина, направление которой определяется по правилу правой руки, или буравчика, и связано с осью вращения. Если вращение является равномерным,

то ω=const и точка на окружности поворачивается на равные углы вокруг оси вращения за равные

времена. Время, за которое она совершает полный оборот, т.е. поворачивается на угол 2π,называется периодом движения Т. Выражение (1.15) можно проинтегрировать в пределах от нуля до Т и получить угловую частоту

.

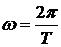Число оборотов в единицу времени есть величина, обратная периоду, — циклическая частота вращения

ν =1/T

Нетрудно получить связь между угловой и линейной скоростью точки. При движении по окружности элемент дуги связан с бесконечно малым поворотом соотношением dS = R·dφ. Подставив его находим

v = ωr

Формула связывает величины угловой и линейной скоростей. Соотношение, связывающее векторы ω и v, следует из рис. А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиусавектора точки r:

.

Таким образом, вектор угловой скорости направлен по оси вращения точки и определяется по правилу правой руки или буравчика.

Угловое ускорение — производная по времени от вектора угловой скорости ω (соответственно вторая производная по

времени от угла поворота) Выразим тангенциальное и нормальное ускорение через угловые скорости и ускорение. Используя связь получаем at = β·R, a =ω2·R

Таким образом, для полного ускорения имеем

Величина β играет роль тангенциального ускорения: если β = 0.полное ускорение при вращении точки не равно нулю, a

=R·ω2 ≠ 0.

3. Закон сохранения импульса.

Зако́н сохране́ния и́мпульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

Рассмотрим второй закон Ньютона

Перепишем его для системы из N частиц:

где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона,

силы вида и будут равны по абсолютному значению и противоположны по направлению, то

есть Тогда после подстановки полученного результата в выражение (1) правая часть будет равна

нулю, то есть:

или

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина

относительно переменной дифференцирования, а значит:

(постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная.

4. Центр инерции системы материальных точек.

Центр масс, центр ине́рции — (в механике) геометрическая точка, характеризующая движение тела или системы частиц как целого.

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется

следующим образом:

где

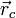— радиус-вектор центра масс,

— радиус-вектор i-й точки системы,

— масса i-й точки.

Для случая непрерывного распределения масс:

где:

— суммарная масса системы,

— объѐм,

— плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

5. Сила. Законы Ньютона.

Зако́ны Ньюто́на — три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих еѐ тел.

Первый закон Ньютона

Существуют такие системы отсчѐта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

Второй закон Ньютона

В инерциальной системе отсчѐта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально еѐ массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

Третий закон Ньютона

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

6. Виды взаимодействий в природе. Силы трения.

Известны четыре вида взаимодействий между элементарными частицами: сильное, электромагнитное, слабое и гравитационное (они перечислены в порядке убывания интенсивности). Интенсивность взаимодействия принято характеризовать так называемой константой взаимодействия α, которая представляет собой безразмерный параметр, определяющий вероятность процессов, обусловленных данным видом взаимодействия. Для электромагнитного взаимодействия константа:

,

где Е – энергия взаимодействия двух электронов, находящихся на расстоянии λ. Следовательно,

.

Тогда характеристическое отношение имеет вид:

.

Константа электромагнитных взаимодействий – безразмерная величина:

.

Константы других видов взаимодействий определяют относительно значения константы электромагнитного взаимодействия.

Отношение констант даѐт относительную интенсивность соответствующих взаимодействий.

Сильное взаимодействие. Этот вид взаимодействия обеспечивает связь нуклонов в ядре. Константа сильного взаимодействия имеет величину порядка 1–10. Наибольшее расстояние, на котором проявляется сильное взаимодействие (радиус действия), составляет примерно м.

Электромагнитное взаимодействие. Константа взаимодействия равна (константа тонкой структуры). Радиус действия не ограничен ( ).

Слабое взаимодействие. Это взаимодействие ответственно за все виды β-распада ядер (включая e-захваты), за распады элементарных частиц, а также за все процессы взаимодействия нейтрона с веществом. Константа взаимодействия равна величине порядка 10–10 – . Слабое взаимодействие, как и сильное, является короткодействующим.

Гравитационное взаимодействие. Константа взаимодействия имеет значение порядка . Радиус действия не ограничен ( ). Гравитационное взаимодействие является универсальным, ему подвержены все без исключения элементарные частицы. Однако в процессах микромира гравитационное взаимодействие ощутимой роли не играет

Сила трения.

Сила, возникающая в месте соприкосновения тел и препятствующая их относительному перемещению, называется силой трения. Направление силы трения противоположно направлению движения. Различают силу трения покоя и силу трения скольжения.

Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения.

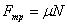, где N — сила реакции опоры, a μ — коэффициент трения скольжения. Коэффициент μ зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения определяется опытным путем.

Сила трения скольжения всегда направлена противоположно движению тела. При изменении направления скорости изменяется и направление силы трения.

Сила трения начинает действовать на тело, когда его пытаются сдвинуть с места. Если внешняя сила F меньше произведения μN,то тело не будет сдвигаться — началу движения, как принято говорить, мешает сила трения покоя. Тело начнет движение только тогда, когда внешняя сила F превысит максимальное значение, которое может иметь сила трения

покоя Трение покоя – сила трения, препятствующая возникновению движению одного тела по поверхности другого.

В некоторых случаях трение полезно (без трения невозможно было бы ходить по земле человеку, животным, двигаться автомобилям, поездам и т.д.), в таких случаях трение усиливают. Но в других случаях трение вредно. Например, из-за него изнашиваются трущиеся детали механизмов, расходуется лишнее горючее на транспорте и т.д. Тогда с трением борются, применяя смазку («жидкостную или воздушную подушку») или заменяя скольжение на качение (поскольку трение каченияхарактеризуется значительно меньшими силами, нежели трение скольжения).

Силы трения, в отличие от гравитационных сил и сил упругости, не зависят от координат относительного расположения тел, они могут зависеть от скорости относительного движения соприкасающихся тел. Силы трения являются непотенциальными силами.

7.Работа и потенциальная энергия.

8.Закон сохранения энергии.

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системыможет быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.

Закон сохранения механической энергии может быть выведен из второго закона Ньютона[5], если учесть, что в консервативной системе все силы, действующие на тело,потенциальны и, следовательно, могут быть представлены в виде

,

где — потенциальная энергия материальной точки ( — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид

,

где — масса частицы, — вектор еѐ скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что , можно получить

Путѐм элементарных операций это выражение может быть приведено к следующему виду

Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.

9. Внутренняя энергия.

Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, еѐ внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:

где

— подведѐнное к телу количество теплоты, измеренное в джоулях 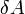[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях

10. Упругие столкновения.

Абсолютно упругие столкновения Для центрального соударения двух тел решение задачи имеет вид[1],[2]

где	— скорости тел до соударения;	— массы двух тел,	— скорости тел после соударения.
Для 'n' тел решение имеет вид[3]

где — номер исследуемого тела системы;

;

.

http://selftrans.narod.ru/v5_1/many_body/many_body65/agfig9.gif

При нецентральном ударе следует учитывать вращающий момент, возникающий за счѐт нецентральности удара, на который распределяется часть энергии и количества движения соударяющихся тел.

11. Абсолютно неупругий удар.

Абсолютно неупругие столкновения Для центрального абсолютно неупругого удара двух тел решение имеет вид[4],[5]

Потеря энергии при ударе определяется теоремой Карно: Кинетическая энергия, потерянная системой тел при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы двигалась с потерянными скоростями[6].

Энергия, которая переходит в нагревание соударяющихся тел вследствие абсолютно неупругого удара, определяется выражением[4]

При нецентральном ударе, как и в случае абсолютно упругого удара, необходимо учитывать вращающий момент, образующийся вследствие нецентральности удара. Он приводит к совместному вращению слипшихся тел после удара.

12. Момент импульса.

Моментом импульса L материальной точки относительно неподвижной точки О называется векторное произведение радиус-вектора r мат. точки, проведенного из точки О на импульс этой мат. точки p=mv

Сумма сил равна произведению массы на укорение a=dV/dt

Сумма F=ma=m(∆V/∆t)= dt

P=Ft= mVколичество движения измеряется в (кг*м)/с

F=dP/dt – второй закон ньютона

Скорость изменения импульса равна изменению сумы сил, дейстующих на это тело!

P=Σ(miVi)=mV F∆t=∆P-импульс силы

Закон сохранения: ΣPi=const L=[rmv]=[rp]

13. Движение в центральном поле.

движения частицы во внешнем поле, в котором ее потенциальная энергия зависит только от расстояния r до определенной неподвижной точки; такое поле называют центральным. Сила

F = − = − ,

действующая на частицу, по абсолютной величине зависит при этом тоже только от r и направлена в каждой точке вдоль радиус-вектора.

При движении в центральном поле сохраняется момент системы относительно центра поля. Для одной частицы это есть М = [rр].

Поскольку векторы М и r взаимно перпендикулярны, постоянство М означает, что при движении частицы ее радиус-вектор все время остается в одной плоскости — плоскости, перпендикулярной к М.

Таким образом, траектория движения частицы в центральном поле лежит целиком в одной плоскости. Введя в ней полярные координаты r, φ, напишем функцию Лагранжа в виде

L = (2 + r 2 2) − U(r ). (14.1)

Эта функция не содержит в явном виде координату φ. Всякую обобщенную координату не входящую явным образом в лагранжеву функцию, называют циклической. В силу уравнения Лагранжа имеем для такой координаты:

=

= 0,

Т.е. соответствующий ей обобщенный импульс pi = ∂L/∂i является интегралом движения. Это обстоятельство приводит к существенному упрощению задачи интегрирования уравнений движения при наличии циклических координат.

В данном случае обобщенный импульс

рφ = mr 2

совпадает с моментом Mz = М, так что мы возвращаемся к известному уже нам закону сохранения момента

М = mr 2 = const.

(14.2)

Заметим, что для плоского движения одной частицы в центральном поле этот закон допускает простую геометрическую интерпретацию. Выражение (1/2)r•rdφ представляет собой площадь сектора, образованного двумя бесконечно близкими радиус-векторами и элементом дуги траектории (рис. 8).

Рис. 8

Обозначив ее как dƒ, напишем момент частицы в виде

М = 2m ,

(14.3)

где производную называют векториальной скоростью. Поэтому сохранение момента означает постоянство секториальной скорости — за равные промежутки времени радиус-вектор движущейся точки описывает равные площади (так называемый второй закон Кеплера).

Полное решение задачи о движении частицы в центральном поле проще всего получить, исходя из законов сохранения

энергии и момента, не выписывая при этом самих уравнений движения. Выражая через М из (14.2) и подставляя в выражение для энергии, получим

E =	(	2 + r 2 2) + U(r ) =	+	+ U (r ).	(14.4)
Отсюда
≡	=				(14.5)
или, разделяя переменные и интегрируя
t =				+ const.	(14.6)
Далее, написав (14.2) в виде
d φ =		dt,

подставив сюда dt из (14.5) и интегрируя, находим

φ = + const. (14.7)

Формулы (14.6) и (14.7) решают в общем виде поставленную задачу. Вторая из них определяет связь между r и φ, т.е. уравнение траектории. Формула же (14.6) определяет в неявном виде расстояние r движущейся точки от центра как

функцию времени. Отметим, что угол φ всегда меняется со временем монотонным образом — из (14.2) видно, что никогда не меняет знака.

Выражение (14.4) показывает, что радиальную часть движения можно рассматривать как одномерное движение в поле с «эффективной» потенциальной энергией

Uэф = U(r ) + . (14.8)

Величину М2/(2mr2) называют центробежной энергией. Значения r, при которых

U(r ) + = E (14.9)

определяют границы области движения по расстоянию от центра. При выполнении равенства (14.9) радиальная скорость обращается в нуль. Это не означает остановки частицы (как при истинном одномерном движении), так как угловая

скорость не обращается в нуль. Равенство = 0 означает «точку поворота» траектории, в которой функция r(t) переходит от увеличения к уменьшению или наоборот.

Если область допустимого изменения r ограничена лишь одним условием r≥rmin, то движение частицы инфинитно — ее траектория приходит из бесконечности и уходит на бесконечность.

Если область изменения r имеет две границы rmin и rmax, то движение является финитным и траектория целиком лежит внутри кольца, ограниченного окружностями r=rmax и r=rmin. Это, однако, не означает, что траектория непременно является замкнутой кривой. За время, в течение которого r изменяется от rmax до rmin и затем до rmax, радиус-вектор повернется на угол Δφ, равный, согласно (14.7),

Δφ = 2

.

(14.10)

Условие замкнутости траектории заключается в том, чтобы этот угол был равен рациональной части от 2, т.е. имел вид

Δφ = 2m⁄n, где m, n — целые числа. Тогда через n повторений этого периода времени радиус-вектор точки, сделав m полных оборотов, совпадает со своим первоначальным значением, т.е. траектория замкнется.

Однако такие случаи исключительны, и при произвольном виде U(r) угол Δφ не является рациональной частью от 2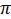. Поэтому в общем случае траектория финитного движения не замкнута. Она бесчисленное число раз проходит через минимальное и максимальное расстояние (как, например, на рис. 9) и за бесконечное время заполняет все кольцо между двумя граничными окружностями.

Рис. 9 Существуют лишь два типа центральных полей, в которых все траектории финитных движений замкнуты. Это поля, в

которых потенциальная энергия частицы пропорциональна 1⁄r или r2. Первый из этих случаев рассмотрен в следующем параграфе, а второй соответствует так называемому пространственному осциллятору.

В точке поворота квадратный корень (14.5) (а вместе с ним и подынтегральные выражения в (14.6) и (14.7)) меняет знак. Если отсчитывать угол φ от направления радиус-вектора, проведенного в точку поворота, то примыкающие с двух сторон к этой точке отрезки траектории будут отличаться лишь знаком φ при каждых одинаковых значениях r; это значит, что траектория симметрична относительно указанного направления. Начав, скажем, от какой-либо из точек r=rmax, мы пройдем отрезок траектории до точки с r=rmin, затем будем иметь симметрично расположенный такой же отрезок до следующей точки с r=rmax и т.д., т.е. вся траектория получается повторением в прямом и обратном направлениях одинаковых отрезков. Это относится и к инфинитным траекториям, состоящим из двух симметричных ветвей, простирающихся от точки поворота rmin до бесконечности.

Наличие центробежной энергии (при движении с М≠0), обращающейся при r→0 в бесконечность, как smallƒrac1r2, приводит обычно к невозможности проникновения движущихся частиц к центру поля, даже если последнее само по себе имеет характер притяжения. «Падение» частицы в центр возможно лишь, если потенциальная энергия достаточно быстро

стремится к − приr→0. Из неравенства

= E − U(r) − > 0

или

r 2U(r) + < Er 2

следует, что r может принимать стремящиеся к нулю значения лишь при условии

r 2U(r)

< −

,

(14.11)

т.е. U(r) должно стремиться к − либо как с >, либо пропорционально − с n>2.

14. Виды движения твердого тела.

Поступательное движение. Поступательным называется такое движение твердого тела, при котором любая прямая, соединяющая две точки тела, дви-жется параллельно самой себе. Траектории точек твердого тела могут быть лю-быми кривыми линиями.

Вращательное движение твердого тела. В р а щ а т е л ь н ы м называ-ется такое движение твердого тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения (колен-чатый вал поршневого двигателя, центробежный компрессор, газовая турбина реактивного двигателя, винт самолета вращаются вокруг неподвижных осей). Угол, отсчитываемый от неподвижной полуплоскости против движения часовой стрелки,

измеряемый в радианах, называется у г л о м п о в о р о т а т е л а - . Уравнение вращения тела вокруг неподвижной оси выражает зави-симость угла поворота от времени (рис. 1.53):

(1.64)

15. Энергия движущегося твердого тела. Теорема Гюйгенса-Штейнера.

Кинетическая энергия твѐрдого тела, вращающегося вокруг неподвижной оси

В твѐрдом теле, вращающемся с угловой скоростью w относительно неподвижной оси z, выделим элемент массой Dmi. Эта частица будет двигаться по окружности радиуса ri с линейной скоростью Vi = wri

Кинетическую энергию тела можно получить, сложив энергии всех его частиц:

.

Здесь = Iz — момент инерции тела относительно оси z, поэтому выражение кинетической энергии вращающегося тела окончательно представим так:

.

(10.6)

Этот результат напоминает формулу кинетической энергии поступательно движущегося тела:

. (10.7)

Различие только в том, что в одном случае при расчѐте энергии используется масса тела и линейная скорость, в другом — момент инерции и угловая скорость вращения.

Кинетическая энергия тела при плоском движении Любое движение твѐрдого тела может быть представлено суперпозицией двух движений — поступательного и вращательного.

Представим плоское движение тела суммой поступательного со скоростью , равной скорости центра масс, и вращения

с угловой скоростью вокруг оси, проведѐнной через центр масс тела — точку С.

Скорость i-той частицы тела (Dmi) будет равна векторной сумме еѐ скоростей в этих двух движениях:

.

Здесь — радиус-вектор частицы, определяющий еѐ положение относительно точки центра масс — С (рис. 10.4).

Рис. 10.4

Вычислим кинетическую энергию i-той частицы:

.

Заметим (см. рис. 10.4), что модуль векторного произведения равен:

,

где Ri — радиус круговой траектории частицы Dmi, или, что то же самое, — еѐ расстояние от оси вращения. Теперь раскроем скобки, попутно сделав циклическую перестановку сомножителей во втором слагаемом: Кинетическая энергия тела равна сумме энергий всех еѐ частиц, поэтому:

.

Анализируя этот результат, приходим к следующим выводам:

Сумма = М равна массе тела.

Сумма равна произведению массы тела на радиус-вектор точки центра масс . Но так как в этой задаче все радиус-векторы откладываются от точки центра масс, то = 0, и = = 0.

Сумма = IC представляет собой момент инерции тела относительно оси вращения, проходящей через центр масс (точку С).

Таким образом, кинетическая энергия тела равна:

. (10.8)

Представив движение суммой поступательного и вращательного движений, мы пришли к выводу, что кинетическая энергия плоского движения равна сумме энергий поступательного движения со скоростью, равной скорости центра масс VС и вращения относительно оси, проходящей через центр масс тела:

.

Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

где

— известный момент инерции относительно оси, проходящей через центр масс тела,

— искомый момент инерции относительно параллельной оси,

— масса тела,

— расстояние между указанными осями. Момент инерции по определению

Радиус-вектор

можно расписать как сумму двух векторов:

,

где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:

Вынося за сумму , получим:

Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:

Тогда:

Откуда и следует искомая формула:

,

где — известный момент инерции относительно оси, проходящей через центр масс тела.

16,17. Вычисление моментов инерции: тонкий однородный стержень, однородная тонкая пластина и прямоугольный параллелепипед.

Вычисление моментов инерции: бесконечно тонкие кольцо и диск, цилиндр.

Рассмотрим теперь проблему определения момента инерции различных тел. Общая формула для нахождения момента инерции объекта относительно оси z имеет вид

Иными словами, нужно сложить все массы, умножив каждую из них на квадрат ее расстояния до оси (x2i + y2i). Заметьте, что это верно даже для трехмерного тела, несмотря на то, что расстояние имеет такой «двумерный вид». Впрочем, в большинстве случаев мы будем ограничиваться двумерными телами.

В качестве простого примера рассмотрим стержень, вращающийся относительно оси, проходящей через его конец и перпендикулярной к нему (фиг. 19.3). Нам нужно просуммировать теперь все массы, умноженные на квадраты расстояния х (в этом случае все у — нулевые). Под суммой, разумеется, я имею в виду интеграл от х2, умноженный на «элементики» массы. Если

мы разделим стержень на кусочки длиной dx, то соответствующий элемент массы будет пропорционален dx, а если бы dx составляло длину всего стержня, то его масса была бы равна М. Поэтому

Размерность момента инерции всегда равна массе, умноженной на квадрат длины, так что единственная существенная величина, которую мы вычислили, это множитель 1/3.

А чему будет равен момент инерции I, если ось вращения проходит через середину стержня? Чтобы найти его, нам

снова нужно взять интеграл, но уже в пределах от —1/2L до +1/2L. Заметим, однако, одну особенность этого случая. Такой стержень с проходящей через центр осью можно представлять себе как два стержня с осью, проходящей через конец,

причем масса каждого из них равна М/2, а длина равна L/2. Моменты инерции двух таких стержней равны друг другу и вычисляются по формуле (19.5). Поэтому момент инерции всего стержня равен

Таким образом, стержень гораздо легче крутить за середину, чем за конец. Моменты инерции

Шар: k = 2/5,

Диск: k = 1/2,

Стержень:

Обруч:

Сфера:

Рис. 6.6

При вычислении момента инерции тела, вращающегося вокруг оси, не проходящей через центр инерции (рис. 6.7), следует пользоваться теоремой о параллельном переносе осей, или теоремой Штейнера основным уравнением динамики поступательного движения

Эта теорема называется теоремой о параллельном переносе оси. Доказывается она очень легко. Момент инерции относительно любой оси равен сумме масс, умноженных на сумму квадратов х и у, т. е. I = Σmi(x2i + y2i). Мы сейчас сосредоточим наше внимание на х, однако все в точности можно повторить и для у. Пусть координата х есть расстояние данной частной точки от начала координат; посмотрим, однако, как все изменится, если мы будем измерять расстояние х` от центра масс вместо х от начала координат. Чтобы это выяснить, мы должны написать

xi = x`i + Xц.м.

Возводя это выражение в квадрат, находим x2i = x`2i + 2Xц.м.x`i + X2ц.м.

Что получится, если умножить его на mi и просуммировать по всем r? Вынося постоянные величины за знак суммирования, находим

Ix = Σmix`2i + 2Xц.м.Σmix`i + X2ц.м.Σmi

Третью сумму подсчитать легко; это просто МХ2ц.м. . Второй член состоит из двух сомножителей, один из которых Σmix`i; он равен x`-координате центра масс. Но это должно быть равно нулю, ведь х` отсчитывается от центра масс, а в этой системе координат среднее положение всех частиц, взвешенное их массами, равно нулю. Первый же член, очевидно, представляет собой часть х от Iц. Таким образом, мы и приходим к формуле (19.7).

Давайте проверим формулу (19.7) на одном примере. Просто проверим, будет ли она применима для стержня. Мы уже нашли, что момент инерции стержня относительно его конца должен быть равен ML2/3. А центр масс стержня, разумеется, находится на расстоянии L/2. Таким образом, мы должны получить, что ML2/3=ML2/12+M(L/2)2. Так как одна четвертая + одна двенадцатая = одной третьей, то мы не сделали никакой грубой ошибки.

Кстати, чтобы найти момент инерции (19.5), вовсе не обязательно вычислять интеграл. Можно просто предположить, что он равен величине ML2, умноженной на некоторый неизвестный коэффициент γ. После этого можно использовать рассуждения о двух половинках и для момента инерции (19.6) получить коэффициент 1/4γ. Используя теперь теорему о параллельном переносе оси, докажем, что γ=1/4γ + 1/4, откуда γ=1/3. Всегда можно найти какой-нибудь окольный путь!

При применении теоремы о параллельных осях важно помнить, что ось Iц должна быть параллельна оси, относительно которой мы хотим вычислять момент инерции.

Стоит, пожалуй, упомянуть еще об одном свойстве, которое часто бывает очень полезно при нахождении момента инерции некоторых типов тел. Оно состоит в следующем: если у нас есть плоская фигура и тройка координатных осей с началом координат, расположенным в этой плоскости, и осью z, направленной перпендикулярно к ней, то момент инерции этой фигуры относительно оси z равен сумме моментов инерции относительно осей х и у. Доказывается это совсем просто. Заметим, что