ЛЕКЦИЯ 12. ПРИБЛИЖЕНИЕ ФУНКЦИЙ СПЛАЙНАМИ.
ЛИТЕРАТУРА. Учебник [1] §§11.11
§12.1 Кубические сплайны.
Потребность в наличии аппроксимирующих функций, которые сочетали бы в себе локальную простоту многочлена невысокой степени и глобальную на всем отрезке [a,b] гладкость, привела к появлению в 1946 году так называемых сплайн-функций или сплайнов. Получив в 60-х годах 20 века распространение как средство интерполяции сложных кривых, к настоящему времени стали важной составной частью самых различных вычислительных методов и нашли широчайшее применение в решении разнообразных научно-технических и инженерных задач.
ОПРЕДЕЛЕНИЕ,
Сплайном степени m
называется функция
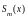 обладающая следующими свойствами:
обладающая следующими свойствами:
1) Функция
непрерывна на [a,b]
вместе со своими производными
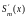 ,
, ,…,
,…,
 до некоторого порядка p.
до некоторого порядка p.
2) На каждом отрезке
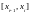 функция
совпадает с некоторым алгебраическим
многочленом
функция
совпадает с некоторым алгебраическим
многочленом
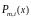 степени m.
степени m.
3)
 ,
i=0,1,…n.
,
i=0,1,…n.
ОПРЕДЕЛЕНИЕ. Разность m-p между степенью сплайна и наивысшим порядком непрерывной на [a,b] производной называется дефектом сплайна.
Простейший пример сплайна дает кусочно-линейная функция, являющаяся сплайном первой степени (линейным сплайном) с дефектом, равным 1.
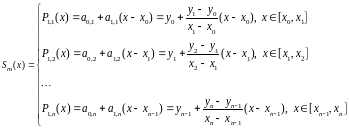
Наиболее широкое распространение получили сплайны третьей степени с дефектом равным 1 или 2.
Термин сплайн происходит от английского слова «spline» (гибкая линейка).
Примером кубического сплайна является интерполяционный многочлен Эрмита.
Так как он строился из условия
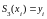 ,
,
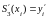 ,
i=0,1,…n.
,
i=0,1,…n.
То есть это кубический сплайн дефекта 2. Его также называют локальным сплайном.
ОПРЕДЕЛЕНИЕ.
Значение производной
в точках
 называют
наклоном сплайна в точке
и обозначают
называют
наклоном сплайна в точке
и обозначают
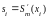 .
.
Построим кубический сплайн дефекта 1.
Заметим,
что на отрезке интерполяции
кубический сплайн однозначно определяется
заданием значений
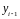 ,
, ,
,
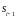 ,
,
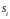 .
Запишем многочлен Эрмита, в котором
заменим известные значения
.
Запишем многочлен Эрмита, в котором
заменим известные значения
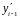 и
и
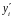 неизвестными
наклонами
и
.
неизвестными
наклонами
и
.
Построение многочлена эрмита
Рассмотрим отрезок интерполяции
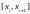 .
Будем считать, что длина отрезка
.
Будем считать, что длина отрезка
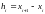 ,
и в концах отрезка известны не только
значения функции
,
и в концах отрезка известны не только
значения функции
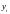 и
и
 ,
но и значения производных:
,
но и значения производных:
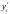 и
и
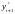 ,
то есть оба узла кратности 2.
,
то есть оба узла кратности 2.
Построим многочлен
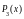 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
 ,
,
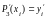 ,
,
,
,

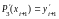 (11.10)
(11.10)
Окончательно, полином запишется так:
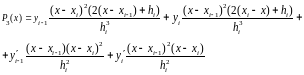 (11.11)
(11.11)
Полученный полином называется полиномом Эрмита.
Теперь в полиноме Эрмита заменим известные значения и неизвестными наклонами и .
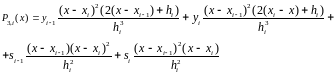
Очевидно, что выполнены следующие равенства:
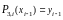 ,
,
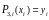
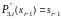 ,
,
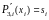
Запишем формулу для сплайна на следующем отрезке.
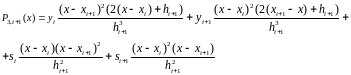
Очевидно, что:
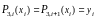 - известное значение ,
- известное значение ,
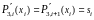 - неизвестное значение.
- неизвестное значение.
Теперь выберем значения наклонов таким образом, чтобы выполнялось равенство и для вторых производных:

Для
этого найдем вторые производные от
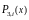 и
и
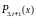 .
.
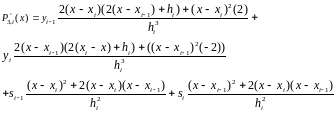
Для второй производной получим следующее соотношение:
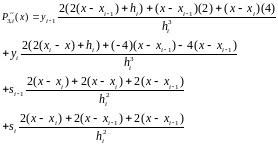
Окончательно,
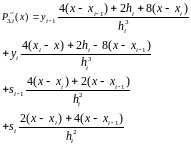
Аналогично найдем вторую производную от :
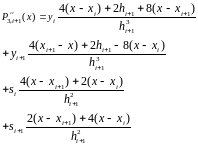
Теперь приравняем значения производных в точке :

Собирая коэффициенты, получим систему линейных алгебраических уравнений для определения наклонов сплайна:
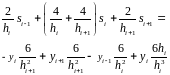
Окончательно, система примет следующий вид:
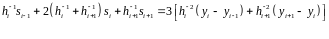
Заметим, что в этой системе (n+1) неизвестное, и (n-1) уравнение.

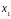
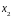
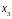 …….
…….

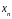
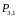
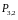
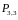
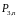
Поставим дополнительные условия:
1. Фундаментальный кубический сплайн.
Известны
значения производной в концах отрезка
:
 и
и
 .
.
Тогда
дополнительные условия выглядят так:
 ,
,
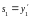 .
.
2.Сплайн с известными значениями второй производной в концах отрезка:
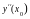 ,
,
 .
.
Тогда дополнительные условия выглядят так: (берем вторые производные в концах отрезка)
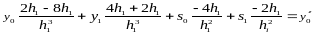
Или:
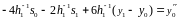
Аналогично
для точки
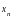 :
:
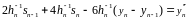
3.
Естественный кубический сплайн:
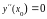 ,
,
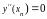
4. Если нет дополнительной информации, то применяют условие «отсутствия узла»:
Выбор
наклонов
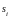 производят таким образом, чтобы для
получаемого сплайна выполнялись условия:
производят таким образом, чтобы для
получаемого сплайна выполнялись условия:
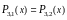 и
и
 .
.
Потребуем для этого совпадения третьих производных в соответствующих точках:
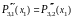 и
и
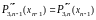 .
.
Тогда получим следующие соотношения:


Погрешность приближения функции кубическими сплайнами.
ТЕОРЕМА.
Пусть функция f
имеет на отрезке [a,b]
непрерывную производную четвертого
порядка и
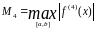 .
Тогда для интерполяционного кубического
сплайна
.
Тогда для интерполяционного кубического
сплайна
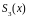 , удовлетворяющего граничным условиям
1,2,4 справедлива следующая оценка
погрешности:
, удовлетворяющего граничным условиям
1,2,4 справедлива следующая оценка
погрешности: