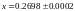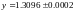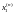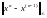§12.2 Решение нелинейных систем уравнений.

Рассмотрим систему нелинейных уравнений.

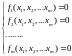(5)

Ее можно записать в матричной форме: 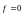, если ввести вектор-функцию

(6)

Рассмотрим различные способы решения системы, основанные на уже известных, изученных методах решения задачи.

ПРИМЕР 1. Найти решение системы уравнений:

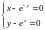
Локализуем корни уравнения.

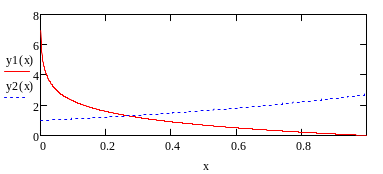
Преобразование системы к виду, удобному для итераций:

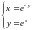
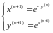
Из представленного графика следует, что:

, .

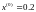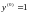Далее считаем нелинейным методом Зейделя:

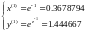, далее:

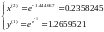
Дальше вычисления сведем в таблицу:

n
0	0.2	1
1	0.3678794	1.444667	0.44
2	0.2358245	1.2659521	0.18
3	0.2819707	1.3257399	0.06
4	0.26560636	1.30422156	0.02
5	0.2713837	1.31177831	0.007
6	0.26934066	1.3091010	0.002
7	0.27006273	1.310046	0.0009

Метод сходится очень медленно.

Метод эквивалентен модифицированному методу простой итерации.

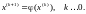
Вернемся к теореме о сходимости метода простой итерации.

Если в окрестности корня функция 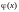непрерывно дифференцируема и удовлетворяет условию

,

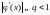то метод простой итерации сходится .

Для систем нелинейных уравнений метод имеет тот же вид, понимаемый в векторной форме:

,

где 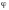- это вектор-функция, которая для данного примера имеет вид: 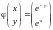. Проверим условие сходимости:

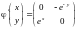
Ясно, что на отрезке локализации корня.

В этом случае 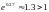условие сходимости не выполнено. Но метод все-таки сходится.

Попробуем воспользоваться более быстро сходящимся методом.

Вернемся к исходной системе (1) и разложим каждую функцию в ряд Тейлора, оставив только линейную часть этого разложения:

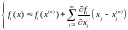
Тогда придем к системе линейных алгебраических уравнений:

Если ввести в рассмотрение матрицу Якоби: ,

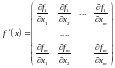то метод Ньютона можно записать в следующей векторной форме:

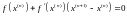
Если предположить, что матрица 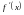невырожденная, то существует

обратная матрица 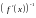и вычисления можно делать по формуле:

.

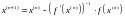ПРИМЕР 2.Найти решение системы уравнений методом Ньютона.

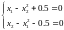
Локализация корней.

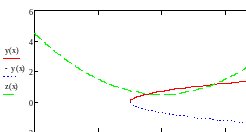
Имеются две точки локализации (-0.5, 0.5) и (1,1).

Найдем матрицу Якоби для задачи:

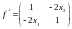
Обратная матрица :

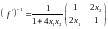
Окончательно , расчетная формула метода примет вид:

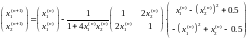
Итерируя по формуле, можно найти решения системы:

(-0.3573;0.37769) и (1.2181;0.98396)

Обычно процесс вычислений организуют без использования обратной матрицы, а на основе решения СЛАУ. Введем вектор

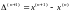
С помощью вектора запишем метод Ньютона так:

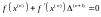
Теперь запишем последнее равенство в виде системы:

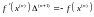
Получили систему нелинейных уравнений. Чтобы ее упростить, возьмем для решения упрощенный метод Ньютона. Для этого вычислим матрицу Якоби в точке начального приближения:

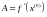
Получили СЛАУ относительно вектора 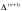. После этого находим

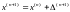. Вычисления выполняем до тех пор пока : .

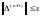Вернемся к примеру.

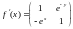. Вычислим матрицу A.

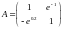
Проведем вычисления:

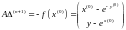
n
0	0.2	1	0.05963444 0.29424043	0.29424043
1	0.25963444	1.29424043	0.00942261 0.01372444	0.01372444
2	0.26905705	1.30796487	0.00071156 0.00163403	0.00163403
3	0.26976861	1.3095989	0.00009433 0.00017768	0.00017768

Ответ: