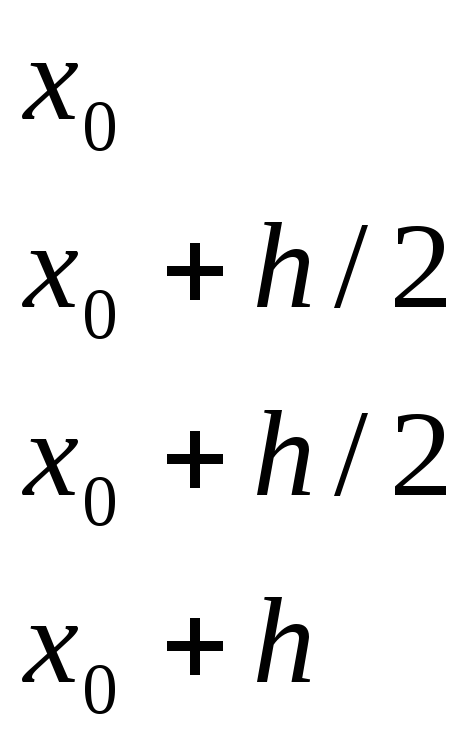1. Квадратурные формулы прямоугольников, трапеций и парабол (формула Симпсона).

- формулы прямоугольников: это простейшие квадратурные формулы, вытекающ из определения опред интеграла, как площади криволинейной трапеции. Разобьем наравных частей, получим,

, тогда

- формула левых прямоугольников

- формула правых прямоугольников

где предельная абсолютная погрешность определяется условием

- формула трапеции

где предельная абсолютная погрешность определяется условием

- формула парабол (формула Симсона). Обязательно должно быть четным.

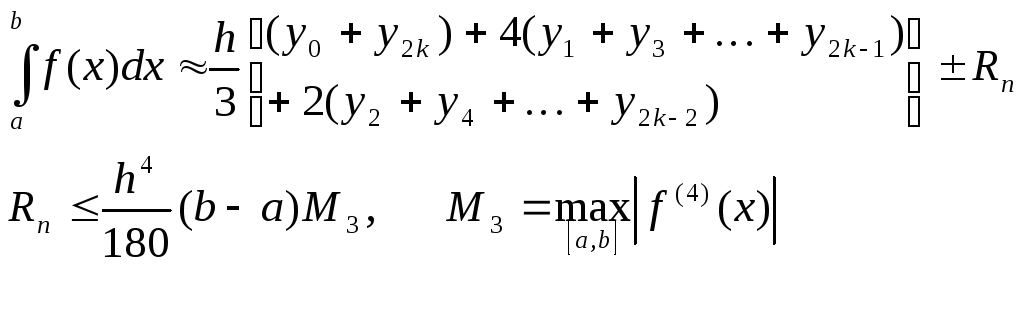
Задача 1.1. Вычислить по формуле Симпсона , принявn=8. Оценить погрешность по методу удвоения шага вычислений. Вычисления вести с пятью знаками после запятой. Сравнить со значением, найденным по формуле Ньютона - Лейбница.

Решение: рассчитаем шаг по формуле .

Рассмотрим подынтегральную функцию

По этим двум формулам подсчитаем значения

	4	4,5	5	5,5	6	6,5	7
	0,33333	0,32038	0,30902	0,29894	0,28990	0,28173	0,027123

* Таблица не влезла, вот её продолжение

	7,5	8
	0,26748	0,26120

*в конце некоторых дробей стоя нули, тем самым показываем что точность 5 знаков после запятой достигнута во всей таблице.

Общий вид формулы имеет вид

Найдем для п=8

Вычисли два интеграла, первый с шагом , обозначим его как, второй с шагом(из условия нахождения погрешности) и обозначим его

Вычислим погрешность

Следовательно искомый интеграл равен

Найдем интеграл по формуле Ньютона – Лейбница

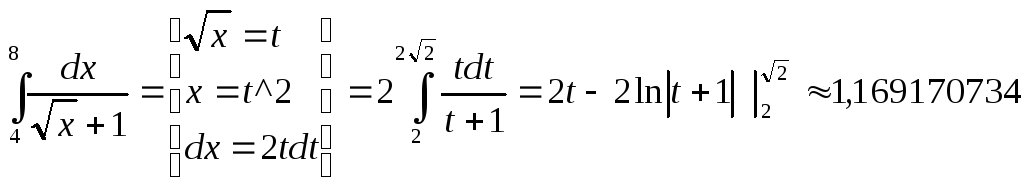
Задача 1.2.Вычислить по формуле Симпсона , принявn=10. Оценить погрешность. Сравнить со значением, найденным по формуле Ньютона - Лейбница.

Решение :

Шаг вычислений

Подынтегральная функция

По этим формулам найдем значения для таблицы

	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
	1	0.90909	0.83333	0.76923	0.71429	0.66667	0.625	0.58824	0.55556	0.52632	0.5

В общем случае формулы нахождения:

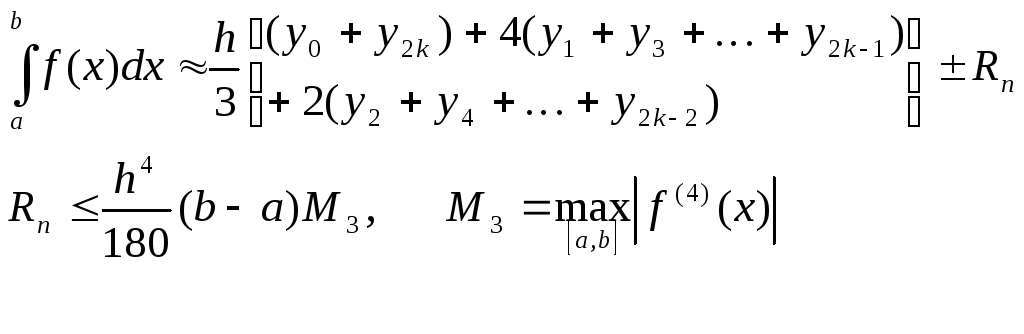
Для случая получим формулы

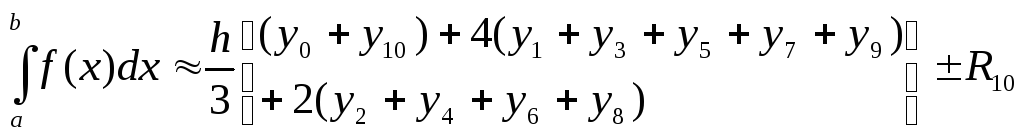
I – значение интеграла без учета погрешности

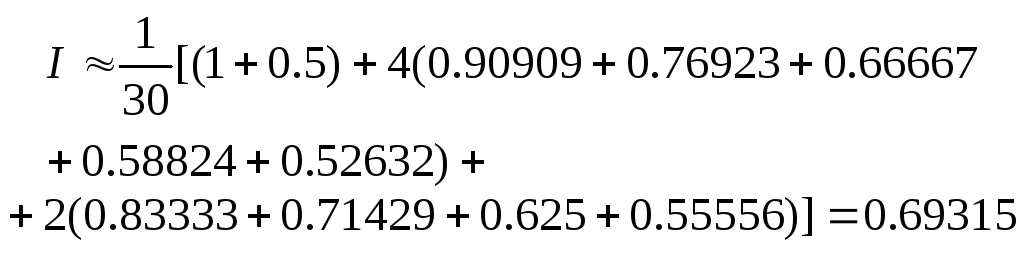
Точное значение находится по формуле Ньютона – Лейбница

Задача 1.3.Вычислить по формуле трапеций принявn=10 . Оценить погрешность. Сравнить со значением, найденным по формуле Ньютона – Лейбница

Решение:

Шаг вычислений

Подынтегральная функция

По этим формулам найдем значения для таблицы

	1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2
	1	1.0488	1.09545	1.14018	1.18322	1.22474	1.26491	1.30384	1.34164	1.3784	1.41421

В общем случае формулы нахождения:

Для случая получим формулы

I – значение интеграла без учета погрешности

е

Точное значение находится по формуле Ньютона – Лейбница

2. Методы Ньютона (касательных) и секущих (хорд) для решения нелинейных уравнений.

Метод секущих

Пусть требуется вычислить действительный корень уравнения, изолированный на отрезке(отделение корня произвольно, любым способом). Рассмотрим график функции, он будет иметь следующий вид, тогда. Соединим точки графикахордой. Уравнение прямой (хорды), проходящей через точкиимеет вид. За приближенное значение искомого корня примем абсциссуточки пересечения хорды АВ, проходящей через точкиимеет вид:

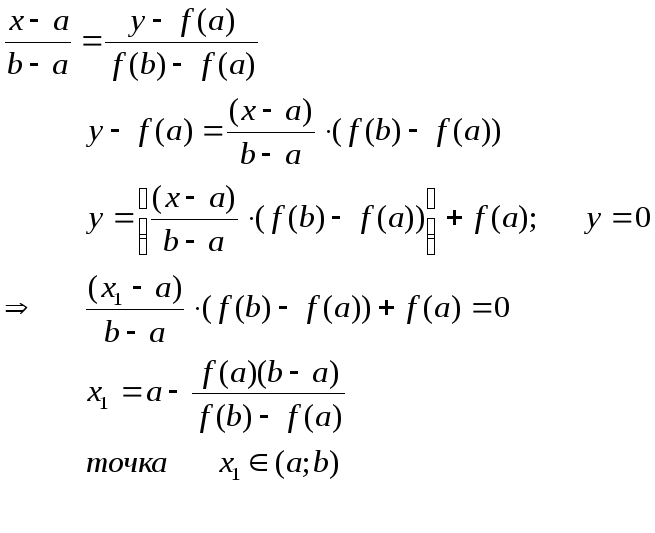
Если , то искомый корень найден,ес ли значении отлично от 0, то метод хорд применяют дальше. Если, то за новый, более узкий отрезок принимаюти соединяют хордой точки

. Точкой пересечения хорды с Ох (её асциссой) будет значение значение , которые вычисляются по формуле

. Этот процесс можно продолжить далее. Полученная последовательность чисел: к искомому корню. Погрешность имеет вид

Где - точный корень,- приближенное значение этого корня.

Метод касательных(Ньютона)

Пусть требуется вычислить действительный корень уравнения , изолированный на отрезке(отделение корня произвольно, любым способом). Функция должна быть непрерывна и её производные тоже до второго порядка включительно, на концах отрезка значения функции должно быть с разными знаками, а первая и вторая производная должны сохранять свой знак на всем рассматриваемом промежутке.

Возьмем на такое числопри которомиимеют тот же знак, что и. Проведем в точкекасательную к кривой, за приближенное значение корня примем абсциссу точки пересечения этой касательной с осью Ох. Тогда получим , зная что уравнение касательной в точкек кривойимеет вид:

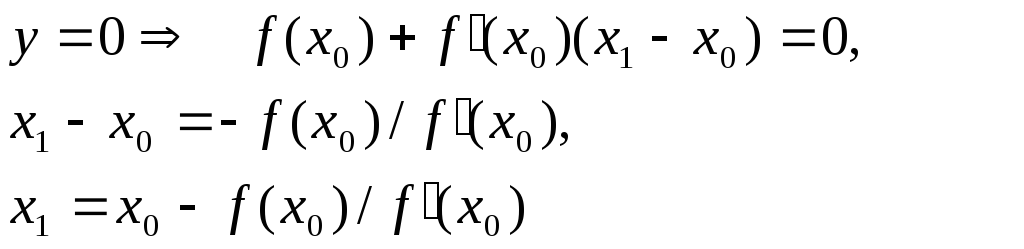
Применяя далее этот прием, получим:

Таким образом получается последовательность чисел, которая имеет своим пределом искомый корень. Оценка погрешности имеет вид

Где - точный корень,- приближенное значение этого корня.

2.1. Отделить корни уравнения графически и уточнить один из них с точностью до 0.001 методом Ньютона(касательных)

Решение:

Разделяем корни уравнения графически

Уточняем корень

Если

Для нахождения x_n используем формулу

Следовательно x=-1.1542 является корнем

3. Численное решение задачи Коши для ОДУ. Примеры методов Рунге-Кутта (методы Эйлера, Эйлера - Коши, Рунге - Кутта 4^го порядка точности).

Простейшим обыкновенным диф уравнением является уравнение вида

Основная задача, относящаяся к этому уравнению, является задача Коши: надо найти такое решение этого уравнения в виде , которое бы удовлетворяло начальному условию.

Метод Эйлера . Пусть дана задача Коши, разделим общий отрезок нап равных частей, выбрав достаточно малый шаг изменения аргумента h, то есть построим начиная с точки равноотстоящих точек.

Вместо искомой интегральной кривой на каждом частичном отрезке буем рассматривать отрезок касательной к этой кривой в соответствующей точке. Возьмем , вместо интегральной кривой инт кривой рассм отрезок касательной к этой кривой в точке, касательная задается уравнением:

При , из этого уравнения можно найти значения

Аналогично, проводя касательную кполучим, проводя рассуждения далее, получим общую формулу

Геометрический смысл данного метода заключается в построении интегральной кривой в виде ломанной с вершинами в точках .

Метод Рунге-Кутта 4^гопорядка точности.

Этот метод является наиболее точным, он заключается в том, что в направлении движения по интегральной кривой вносится несколько поправок. Пусть дана задача Коши

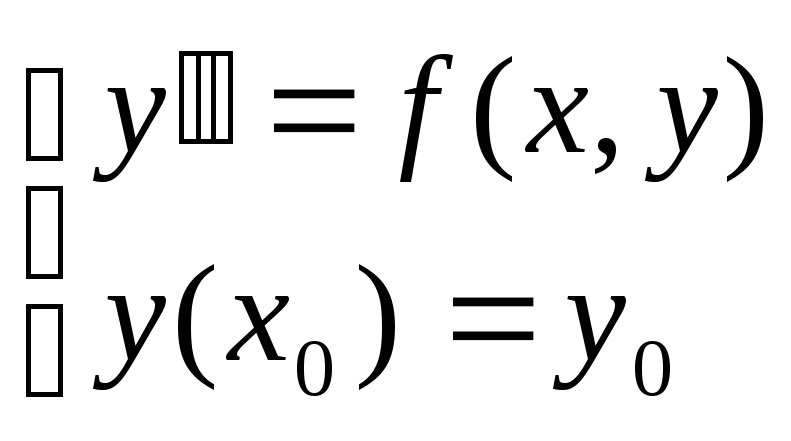
Пи численном интегрировании ОДУ определяют 4 параметра

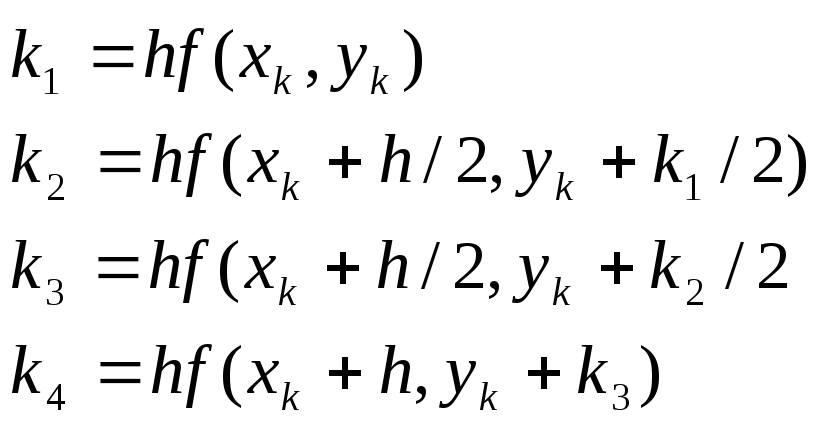
Затем находим

Тогда

Ручные вычисления по этому методу, можно оформить в виде таблице

Задача 3.1.

Методом Рунге – Кутта решить задачу Коши для ОДУ на отрезке [0;0,5] с шагомh=0.1 Вычисления вести с тремя верными знаками

Решение:

Используем вспомогательные коэффициенты

Вычисления оформим в таблице

x	y	k_j=hf(x,y)	y
x_0=0	y_0=1	k_1=0.05	y_0=0.0562
x_0+h/2=0.05	y_0+(k_1)/2=1.025	k_2=0.0561
x_0+h/2=0.05	y_0+(k_2)/2=1.0281	k_3=0.0563
x_0+h=0.1	y_0+(k_3)/2=1.0563	k_4=0.0623

Продолжим вычисления для x_2­

_­­

x_1=0.1	y_1=1.0562	k_1=0.0623	y_0=0.0682
x_1+h/2=0.15	y_1+(k_1)/2=1.0874	k_2=0.0682
x_1+h/2=0.15	y_1+(k_2)/2=1.0903	k_3=0.0683
x_1+h=0.2	y_1+(k_3)/2=1.1245	k_4=0.074

Аналогично высчитываются остальные ­x­₃ , x₄ , x₅

Таким образом

x_0=0 y_0=1

x_1=0.1 y_1=1.0562

x_2=0.2 y_2=1.1927

… … … … …

x_5=0.5 y_5= …

4. Метод простой итерации решения СЛАУ. Достаточные условия сходимости итерационного процесса.

Иногда при решении систем линейных алгебраических уравнений можно воспользоваться числинным итерационным методом, например методом простой итерации. Пусть дана СЛАУ

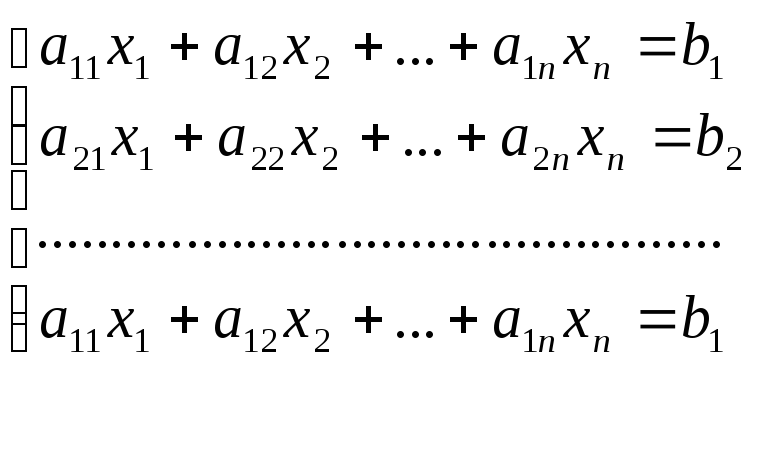(1)

При условии, что число уравнений совпадают с числом неизвестных и основная матрица системы не вырождена. Перепишем систему в виде

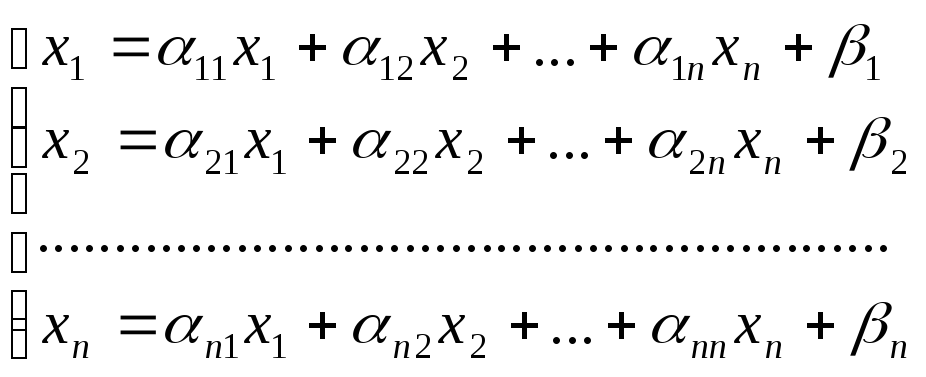(2) сокращенно

Получен системы (2) определяет отображение F : , которая преобразуетп- мерный вектор пространства с координатамив точкус координатамитого же пространства. Используем для решения систему (2). Выберем начальную точкус координатамии построим последовательность.

Последовательность точек

, , …,, … (3)

называется итерационной последовательность п-мерного пространства. При определенных условиях (рассмотрим их ниже) эта может оказаться сходящейся и её придел будет являться решением системы (2).

Условие сходимости(в книги оно написано как необходимое, а в формулировке вопроса задается как достаточное , поэтому я вообще не стала указывать какре оно) модули диагональных коэффициентов системы (1) должны быть значительно больше модулей недиагональных коэффицентов этой системы.