Корректность программы

Как было показано ранее, каждая программа имеет вполне определенное значение. Это значение само по себе не может быть корректным или некорректным

Однако значение программы может совпадать или не совпадать с тем, к чему стремился программист. Таким образом, обсуждение корректности требует рассмотрения подразумеваемого значения программы. Наши предыдущие рассмотрения корректности и полноты всегда соотносились с некоторым подразумеваемым значением.

Подразумеваемое значение программы Р – это некоторое множество основных целей. С помощью подразумеваемого значения мы выделяем те цели, для вычисления которых программа и была создана. Программа P корректна относительно подразумеваемого значения М, если М(Р) содержится в М. Программа Р полна относительно подразумеваемого значения М, если М содержится в М(Р). Таким образом, программа корректна и полна относительно подразумеваемого значения, если эти два значения полностью совпадают.

Другим важным вопросом, относящимся к логическим программам, является вопрос об остановке программы. Назовем областью любое; множество целей (не обязательно основных), замкнутое относительно построения примеров. То есть для любой области D, если А входит в D и А' – пример А, то А’ тоже входит в D.

Областью остановки, программы Р называется такая область D, что каждое вычисление программы Р с каждой целью из D заканчивается.

Обычно полезные программы должны иметь область остановки, охватывающую подразумеваемое значение. Однако поскольку вычислительная модель логических программ не зависит от порядка, в котором редуцируются цели в резольвенте, то большинство интересных логических программ имеют бессодержательную область остановки. Эта ситуация улучшится при рассмотрении языка Пролог. Ограничения, налагаемые на вычислительную модель Пролога, позволяют создавать нетривиальные программы с требуемыми областями остановки.

Рассмотрим программу 3.1 определяющую натуральныe числа. Программа останавливается для любой цели, принадлежащей базису Эрбрана. Однако в области {natural_number(X)} программа не останавливается. Это связано с возможностью незавершающегося вычисления, показанного на рис. 5.1.

При анализе любой логической программы полезно найти области, в которых программа останавливается. Для рекурсивных программ это обычно сделать не просто. Нам нужно ввести описание рекурсивных типов данных, пригодное для исследования проблемы остановки.

Напомним, что тип – это множество термов. Тип называется полным, если данное множество замкнуто относительню построения примеров.

natural_number (X) X=s(Xl)

natural_number(Xl) Xl=s(X2)

natural_number(X2) X2=s(X3)

Рис. 5.1. Незавершающееся вычисление.

Каждому полному типу Т мы сопоставим неполный тип IT, состоящий из термов, имеющих примеры, входящие в Т, и имеющих примеры, не входящие в Т.

Продемонстрируем применение этих понятий на примере определения областей остановки рекурсивных программ, использующих рекурсивные типы. Приведем примеры определений полного и неполного типов для натуральных чисел и списков. Константа 0 и любой терм вида s(0) являются (полным) натуральным числом. Неполным натуральным числом является или переменная X, или терм вида s(X). Программа 3.2, задающая отношение , останавливается в области, состоящей из целей, у которых первый или второй аргумент (или оба) являются полным натуральным числом.

Список является полным, если любой пример данного списка удовлетворяет программе 3.11. Список неполный, если имеются примеры, удовлетворяющие программе 3.11, и примеры, не удовлетворяющие этой программе. Список [а, b, c], например, является полным списком (доказывается на рис. 3.3), в то время как переменная Х – неполный список. Два менее тривиальных примера: [а, X, с] – полный список, хотя и не основной, a [a. B | Xs] – неполный.

1. Областью остановки программы, задающей append, является множество целей, у которых первый или третий аргумент (или оба) являются полными списками.

Сложность

Разнообразные использования логических программ слабо влияют на характер мер сложности. Поэтому вместо описания сложности в терминах длины входа при конкретном использовании программы мы обратимся к выводу целей из значения программы. Естественной мерой сложности логической программы является длина доказательств, порождаемых при выводе целей из значения логической программы.

Начнем рассмотрение с введения нового определения – размера цели. Размер терма – это число символов в текстовой записи терма. Константы и переменные записываются с помощью одного символа и имеют размер 1. Размер составного терма на единицу больше суммы размеров аргументов терма. Например, список [b] имеет размер 3, список [а,b] имеет размер 5, цель append([a,b],[c,d]X) имеет размер 12. В общем случае список из п элементов имеет размер 2п + 1.

Сложность длины вывода программы Р равна L(n), если любая цель G, принадлежащая значению программы и имеющая размер n, может быть выведена из программы Р с длиной вывода, не превосходящей L(n).

Сложность длины вывода связана с обычными мерами сложности в теории алгоритмов. В случае последовательной реализации вычислительной модели эта сложность соответствует временной сложности. Программа 3.15, задающая отношение append, имеет линейную сложность длины вывода. Это показано в упражнении (1) в конце раздела.

Применимость этой меры сложности к программам на Прологе, а не к логическим программам, зависит от использования алгоритма унификации без проверки на вхождение. Рассмотрим процесс вычисления простейшей программы соединения двух списков. Соединение двух списков, как показано на рис. 4.3, использует несколько унификации целей вида append с заголовком правила append – append([X | Xs],Ys,[X | Zs]). Потребуется не менее трех унификаций, сопоставляющих переменные со списками (возможно, неполными). Если в каждой унификации должна быть выполнена проверка на вхождение, то списки, соответствующие аргументам, будут найдены. Время этого процесса прямо пропорционально размеру входной цели. Однако если проверка на вхождение не производится, то время унификации ограничено константой. Общая сложность append-вычисления квадратично зависит от размера входных списков при использовании проверки на вхождение и линейно - без использования проверки.

Введем другие полезные меры сложности, основанные на доказательстве. Пусть R – доказательство. Назовем глубиной R самое глубокое использование цели в некоторой резолюции, размер цели в R – максимальный размер редуцируемых в R целей.

Логическая программа Р имеет сложность размера цели G(n), если любая цель А, принадлежащая значению программы и имеющая размер n, может быть выведена из программы Р так, что размер цели в выводе не превысит G(n).

Логическая программа Р имеет сложность глубины вывода D(n) если любая цель А, принадлежащая значению программы и имеющая размер п, может быть выведена из программы Р с глубиной вывода, не превосходящей D(n).

Сложность размера цели связана с емкостью памяти. Сложность глубины вывода связана с объемом запоминаемой информации при последовательных реализациях и с емкостной и временной сложностью при параллельных реализациях.

Деревья поиска

В рассматривавшихся до сих пор вычислениях логических программ проблема недетерминизма всегда разрешалась корректным выбором. Например, в мерах сложности, основанных на дереве доказательства, предполагалось, что для проведения редукции из программы может быть выбрано нужное предложение. Другой способ вычислительного моделирования недетерминизма состоит в параллельном рассмотрении всех возможных редукций. В этом разделе мы рассмотрим деревья поиска – формализм, подходящий для исследования всевозможных путей вычисления.

Дерево поиска цели G относительно программы Р определяется следующим образом. Корнем дерева является G. Вершины дерева образуют цели (возможно, конъюнктивные) с одной выделенной целью. Для каждого предложения, заголовок которого унифицируем с целью, выделенной в вершине N, имеется ребро, ведущее из вершины N. Каждая ветвь дерева соответствует вычислению цели G относительно программы Р. Листья дерева называются успешными вершинами, если цель, соответствующая листу, пуста, и безуспешными вершинами, если, цель, выделенная в вершине, не может быть редуцирована. Успешные вершины соответствуют решениям корня дерева.

В общем случае для одной и той же цели и одной и той же программы имеется много деревьев поиска. На рис. 5.2 приведены два дерева поиска при решении вопроса сын (S,аран)? с помощью программы 1.2. Два дерева соответствуют двум выборам цели для редукции в резольвенте отец(аран,S), мужчина(S). Деревья различны, но в обоих – единственная успешная ветвь, соответствующая решению вопроса, – S = лот. Соответствующие успешные ветви приведены в виде протоколов на рис. 4.4.

Рис. 5.2. Два дерева поиска.

Мы придерживаемся некоторых соглашений при изображении деревьев поиска. Самая левая цель в вершине всегда выделена. Следовательно, в производных целях цели могут быть переставлены так, чтобы первой стояла цель, выбранная для редукции. На ребрах дерева записываются подстановки, применяемые к переменным самой левой цели. Эти подстановки вычисляются в процессе работы алгоритма унификации.

В случае детерминированных вычислений деревья поиска тесно связаны с протоколами вычислений. Протоколы вычислений аррепd-целей и hanoi-целей, приведенные соответственно на рис. 4.3 и 4.5, могут быть легко преобразованы в деревья поиска.

Дерево поиска содержит несколько успешных вершин, если вопрос имеет несколько успешных решений. На рис. 5.3 приведено дерево поиска для вопроса append(As,Bs,[a,b,c]) относительно программы 3.15, определяющей отношение append. Вопрос состоит в расщеплении списка [a,b,c] на два списка. Совокупность меток на ребрах, ведущих в успешную вершину, задает решения для As и Вs. Например, самая левая ветвь дерева на рисунке соответствует решению {Аs = [a,b,c], Bs = [ ]}.

Число успешных вершин в различных деревьях поиска для данной цели и данной программы одинаково.

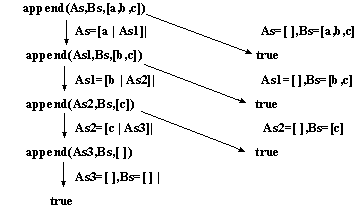
Рис. 5.3. Дерево поиска с многочисленными успешными вершинами.

Дерево поиска может иметь бесконечные ветви, которые соответствуют незавершающимся вычислениям. Рассмотрим цель append(Xs,[c,d],Ys) относительно обычной программы, задающей отношение append. Дерево поиска приведено на рис. 5.4, Бесконечная ветвь соответствует незавершающемуся вычислению, показанному на рис. 4.6

Рис. 5.4. Дерево поиска с бесконечной ветвью.

В терминах деревьев поиска можно определять меры сложности. В программах на Прологе применяется обход дерева в глубину. Поэтому меры сложности, основанные на размере дерева поиска, точнее отражают реальную сложность программ на Прологе, чем меры, основанные на сложности дерева вывода. Однако анализировать сложность дерева поиска гораздо труднее.

Данный вопрос связан с серьезной проблемой. Дело в том, что взаимосвязь между деревьями поиска и деревьями вывода отражает взаимосвязь между детерминированными и недетерминированными вычислениями. Вопрос о совпадении классов сложности, определяемых в терминах деревьев вывода, с классами сложности, определяемыми в терминах деревьев поиска, является классическим вопросом «Р =NP», переформулированным в терминах логического программирования.

Отрицание в логическом программировании

Логическая программа является совокупностью правил и фактов, описывающих истинные утверждения. Ложные факты явно не указываются, они просто опускаются. В данном разделе мы опишем расширение вычислительной модели логического программирования, допускающее ограниченное использование отрицательной информации в программах.

Определим отношение not G и опишем его значение. Данное отрицание является частным случаем отрицания в логике первого порядка. Отношение not трактует отрицание как отсутствие. Цель not G считается выводимой из программы Р, если G не выводима из Р.

Опишем отрицание как отсутствие в терминах дерева поиска. Дерево поиска цели G относительно программы Р называется конечно-безуспешным, если в дереве нет успешных вершин и нет бесконечных ветвей. Конечно-безуспешным множеством логической программы Р называется множество тех целей, для которых имеется конечно-безуспешное дерево поиска относительно программы Р.

Цель not следует из программы Р при понимании отрицания как отсутствия, если G входит в конечно-безуспешное множество программы Р.

Рассмотрим простой пример. Возьмем программу, состоящую из двух фактов:

любит (авраам, гранаты).

любит (исаак, гранаты).

Цель not любит (сара, гранаты) следует из программы при понимании отрицания как отсутствия. Дерево поиска любит (сара, гранаты) имеет одну безуспешную вершину.

Использование отрицания как отсутствия позволяет легко определять многие отношения. Например, отношение disjoint (Xs.Ys), означающее, что у двух списков Xs и Ys нет общих элементов, может быть декларативно определено следующим образом:

disjoint(Xs,Ys)  not(member(X,Xs),member(Y,Ys));

Это означает: «список Xs не пересекается со списком Ys, если никакой элемент Xs не является членом обоих списков Xs и Ys».

Программа 5.1 является другим примером программы, использующей отрицание. В программе определяется отношение неженатый_студент (Человек), означающее, что Человек является неженатым студентом. Вопрос неженатый_студент (Х)?. имеет решение Х = билл.

Построение и корректной, и эффективной реализации отрицания как отсутствия сталкивается с серьезными трудностями. Большинство реализации Пролога таково, что отрицание корректно в простых случаях, но приводит к логически неверным заключениям в более сложных случаях.

неженатый_студент(X)  not женат(X), студент(X),

студент(билл),

женат(джо).

Программа 5.1. Простая программа, использующая not.