Свойства векторного произведения:

1. Векторное произведение антикоммутативно, т.е. [а, b] = - [b, а];

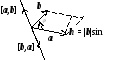2. [а+ b, с] = [а, с] + [b, с];

3. ;

4. [а, b] = 0 тогда и только тогда, когда векторы а и b коллинеарны;

5. (Геометрический смысл векторного произведения). Длина векторного произведения векторов а и b равна площади параллелограмма, построенного на этих векторах.

Док-во: 1. При изменении порядка сомножителей плоскость, в которой лежат сомножители, остается прежней, поэтому остается прежней прямая, перпендикулярная этой плоскости, однако кратчайший поворот от первого сомножителя до второго теперь виден с другой стороны, следовательно, произведение меняет знак;

1. Второе свойство будет доказано позже, после изучения свойств смешанного произведения;

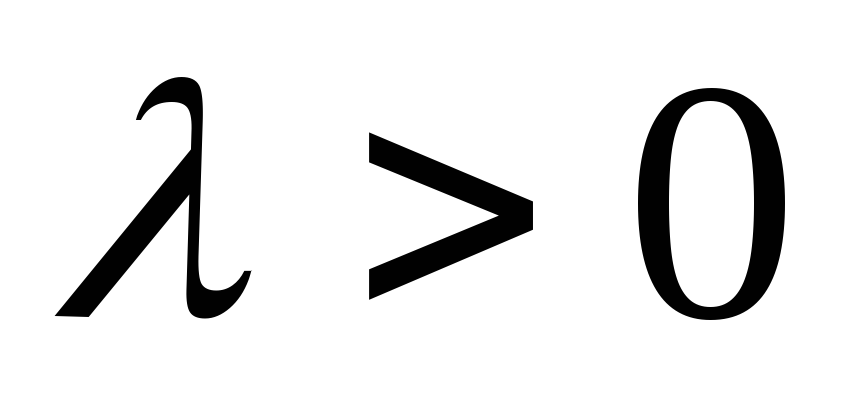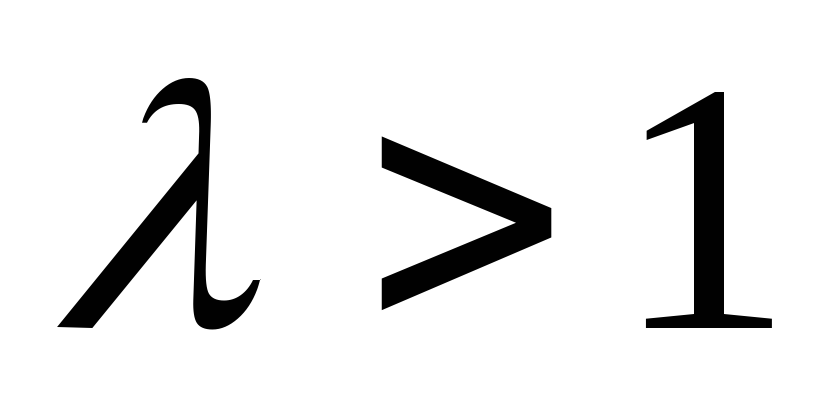2. Если , то вектор [а, b] растягивается (при ) или сжимается (при ) в раз; если 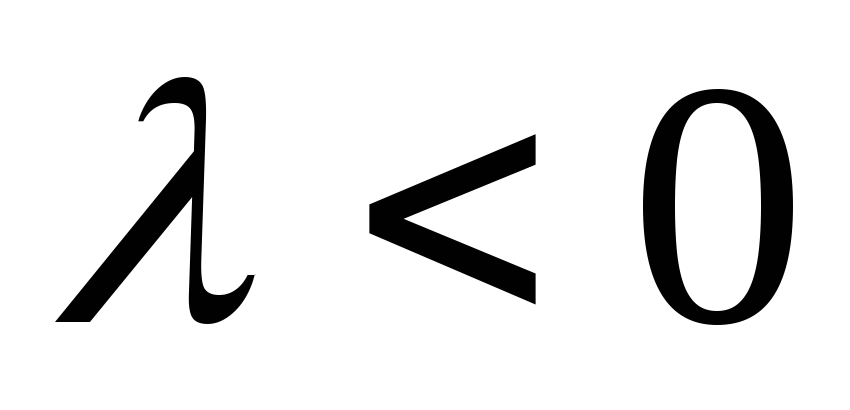, то [а, b] еще меняет и направление;

3. [а, b] = 0, как уже говорилось, тогда и только тогда, когда либо по крайней мере один из этих векторов – нулевой, л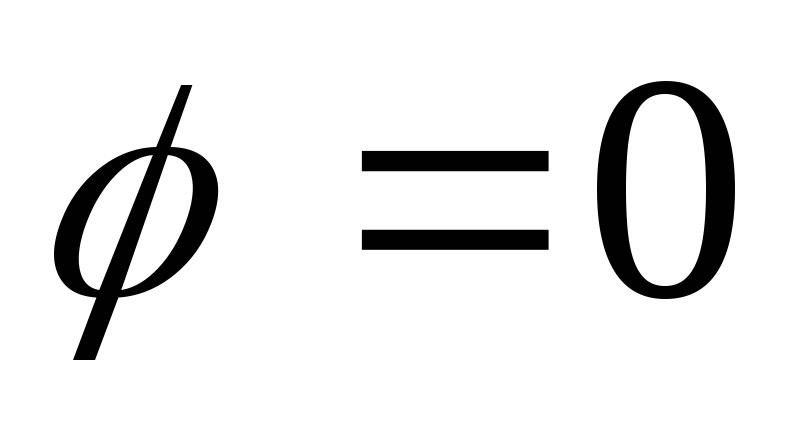ибо , либо ; во всех этих случаях векторы коллинеарны;

4. Если на векторах а и b построить параллелограмм и рассматривать а как основание, то высота параллелограмма равна 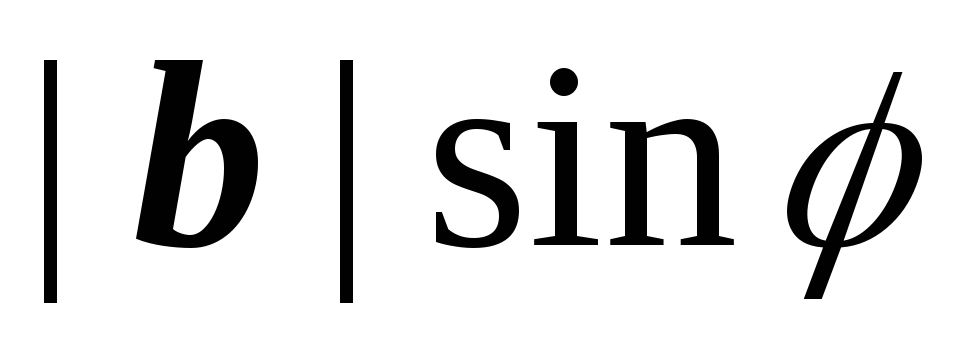. Следствием из пятого свойства является то, что площадь треугольника, построенного на векторах а и b, равна половине длины их векторного произведения.

Механический смысл векторного произведения. Если к точке А приложена сила F, то момент этой силы относительно точки О равен .

Вычисление векторного произведения в правом ортонормированном базисе. Пусть i, j, k – базисные орты. Из картинки справа убеждаемся, что [i, j] = k; [j, k] = i; [k, i] = j. Кроме того, [j, i] = - k; [k, j] = - i; [i, k] = - j, и [i, i] =

=[j, j] = [k, k] = 0.

Пусть а = а_х i + а_у j + а_z k и b = b_х i + b_у j + b_z k. Тогда

[а, b] = [а_х i + а_у j + а_z k, b_х i + b_у j + b_z k] = а_х b_х [i, i] + а_х b_у [i, j] + а_х b_z [i, k] + … + + а_z b_z [k, k] = а_х b_у k + а_х b_z (-j) + а_у b_х (-k) + а_у b_z i + а_z b_х j + а_z b_у (-i) =

= i (а_у b_z - а_z b_у) - j (а_х b_z - а_z b_х) + k (а_х b_у - а_у b_х) = .

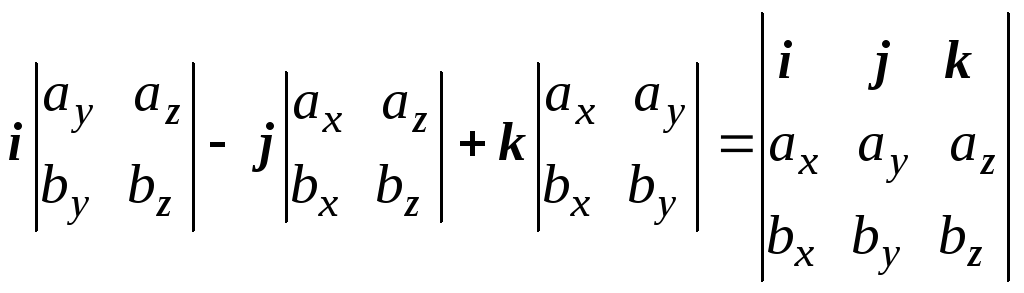Нами доказана

Смешанным произведением векторов a, b, c называется векторно-скалярное произведение ([a, b], c).

Согласно этому определению первые два сомножителя умножаются векторно, затем результат скалярно умножается на третий сомножитель.

Теорема (геометрический смысл смешанного произведения). Модуль смешанного произведения векторов a, b, c равно объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов a, b, c – правая, и отрицательно, если эта тройка – левая (если векторы a, b, c компланарны, то их смешанное произведение равно нулю).

Д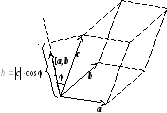ок-во. V_пар = . Справа в этом равенстве стоит модуль смешанного произведения. Знак смешанного произведения определяется знаком косинуса: если тройка a, b, c – правая, то векторы [a, b] и с расположены в одном полупространстве относительно плоскости векторов a и b, , ; если тройка a, b, c – левая, то векторы [a, b] и с расположены в разных полупространствах относительно плоскости векторов a и b, , ; если компланарны, то высота параллелепипеда равна нулю, и V_пар =0.

Из доказанной теоремы следует, что

([a, b], c) = (a, [b, c]), так как для троек a, b, c и

b, c, а совпадают и построенные на них параллелепипеды и ориентации (циклическая перестановка). Следовательно, при сохранении порядка сомножителей не важно, где стоят квадратные скобки, обозначающие векторное произведение. Поэтому их обычно опускают, и обозначают векторное произведение просто или вообще abc.

Итак, abc = саb = bcа = – bаc = – сbа = –аcb.

Отметим еще одно очевидное следствие из теоремы. Объем треугольной пирамиды, образованной векторами a, b, c, вычисляется по формуле .

1.8.2. Свойства смешанного произведения.

1. (а + b)cd = аcd + bcd;

2. ;

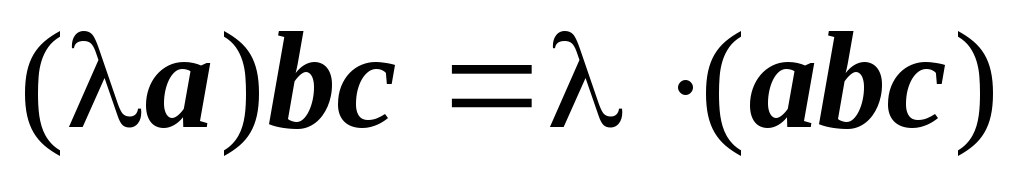3. (Необходимое и достаточное условие компланарности векторов) Смешанное произведение трёх векторов равно нулю тогда и только тогда, когда векторы компланарны;

4. Смешанное произведение не меняется при циклической перестановке сомножителей: abc = = саb = bcа;

5. Смешанное произведение меняет знак при перестановке дух сомножителей:

bаc = – аbс.

Док-во. Первые два свойства следуют из соответствующих свойств скалярного произведения (см. пункт 1.6.2 свойства 4 и 5): (а + b)cd = (а + b, [c, d]) = (а, [c, d]) + (b, [c, d]) =

= аcd + bcd; ; остальные свойства обсуждались выше.

Теперь мы можем доказать второе свойство векторного произведения (см. пункт .7.2. Свойства векторного произведения): [а + b, с] = [а, с] + [b, с]. Покажем, что векторы в левой и правой частях этого равенства имеют одинаковые координаты (тогда, по теореме 1.5.1.о единственности разложения по базису, эти векторы равны). Координаты вектора равны скалярным произведениям этого вектора на базисные орты (см. пункт 1.6.3. Скалярное произведение векторов, заданных в ортонормированном базисе). Находим эти произведения: ([а + b, с], i) (это смешанное произведение, для которого свойство доказано) = ([а, с], i) + ([b, с], i) = (([а, с] + [b, с]), i) – это уже произведение для суммы векторов в правой части доказываемого равенства. Так же доказываются равенства для второй (с ортом j) и третьей координат (c k).

Вычисление смешанного произведения в ортонормированном базисе.

Теорема Смешанное произведение abc векторов а_х i + а_у j + а_z k, b = b_х i + b_у j + b_z k,

с = с_х i + с_у j + с_z k равно определителю .

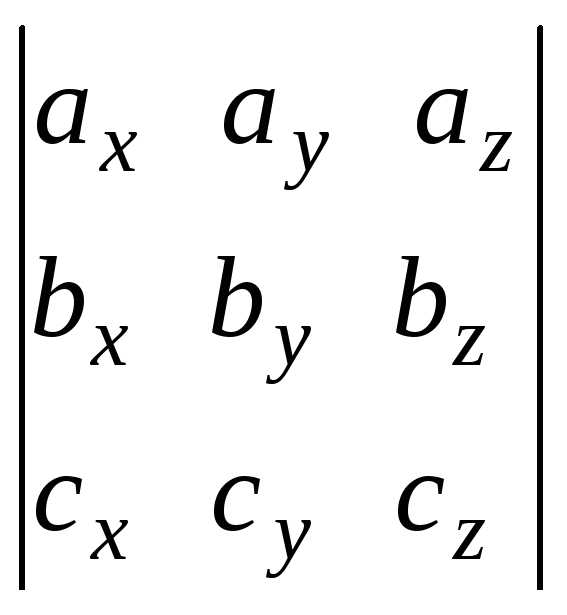Док-во. abc = (a, [b, c]) =

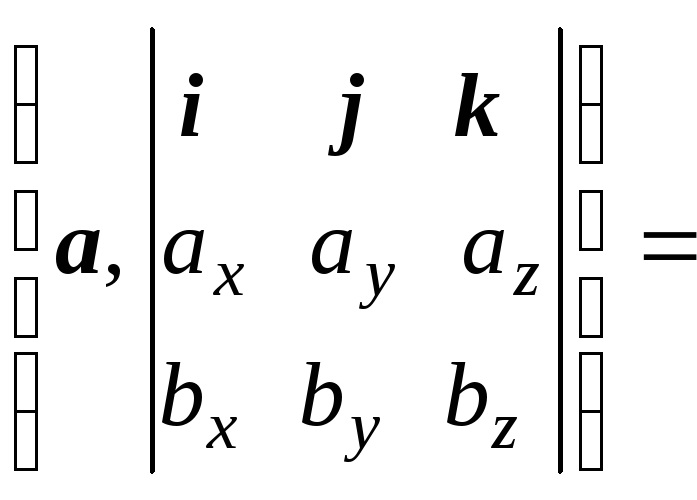
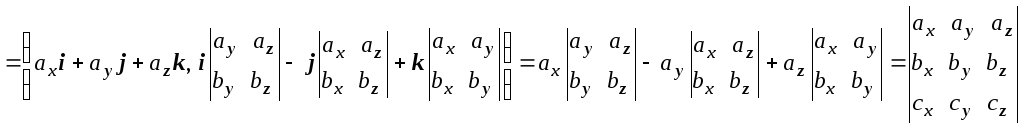
Декартова прямоугольная система координат.

Совокупность точки О (начала координат) и ортонормированного базиса i, j, k, векторы которого отложены из точки О, называется декартовой прямоугольной системой координат в пространстве. Прямые Ох, Оу, Oz, проходящие через точку О в направлении базисных ортов, называются осями координат (осью абсцисс, осью ординат, осью аппликат). Пусть А – произвольная точка пространства. Вектор r_A = ОА = xi + yj + zk называется радиусом-вектором точки А, координаты этого вектора (x, y, z) (равные проекциям вектора на координатные оси) называются также координатами точки А (обозначение: А(x, y, z)).

Р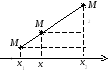асстояние между двумя точками (длина отрезка). Эту задачу мы уже рассматривали. Длина отрезка В₁В₂ (верхний рисунок) равна длине вектора, соединяющего эти точки, т.е.

.

Деление отрезка в данном отношении. Говорят, что точка М делит отрезок М₁М₂ в отношении , если . Найдем координаты точки М. На рисунке справа изображен отрезок и его проекция на ось Ох. Из подобия треугольников . Так же можно получить выражения для координат у, z. Окончательно, координаты точки, делящей отрезок в отношении , равны В частном случае , т.е. когда точка М – середина отрезка, получаем, что координаты середины отрезка равны средним арифметическим координат концов:

Векторное уравнение прямой. Пусть на плоскости задана точка М₀(x₀, у₀) и ненулевой вектор N(A, B). В аналитической геометрии прямая задается как геометрическое место точек М(x, у) таких, что вектор ортогонален вектору N. Таким образом, в векторном виде уравнение прямой записывается так:

(скалярное произведение ортогональных векторов равно нулю).

Дальше мы вернемся к этому уравнению; сначала вспомним, что известно о прямой из школы.