teoria

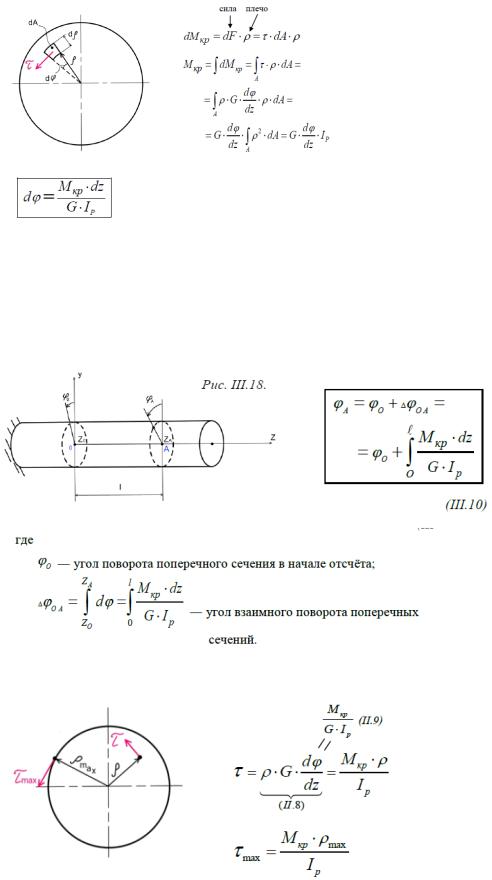
Внутренний крутящий момент Mкр в поперечном сечении стержня есть суммарный результат действия касательных напряжений τ в нём:

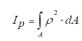полярный момент инерции поперечного (III.9)сечения, [ м4 ]; G I p ― жёсткость стержня при кручении.

Угол поворота произвольного поперечного сечения А:

Напряжения в произвольном поперечном сечении:

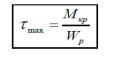
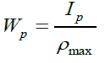полярный момент сопротивления (III.13)

(момент сопротивления при кручении для круглых и кольцевых поперечных сечений), [м3].

19.кручение тонкостенных замкнутых профилей: гипотезы,положенные в основу вывода,связь между крут моментом и касат напряжением: равновесие элемента стержня, вывод формулы для определения касат напряжения, удельная потенц энергия деформации, потенциальная энергия стержня, угол закручивания.

Гипотезы:

1)Касательные нап

2)По толщине стенки напряжения не меняются.

Произведение среднего напряжения на соответствующую толщину стенки в любом месте профиля есть величина постоянная:

Из закрученного бруса выделим элемент двумя продольными и двумя поперечными сечениями (рис. III.22.). Полагаем, что по длине бруса толщина его стенки не меняется. Одно из условий равновесия элемента:

Из вспомогательной теоремы следует, что наибольшее напряжение в сечении тонкостенного замкнутого профиля будет в участке с наименьшей толщиной (рис. III.22.).

Момент сопротивления при кручении:

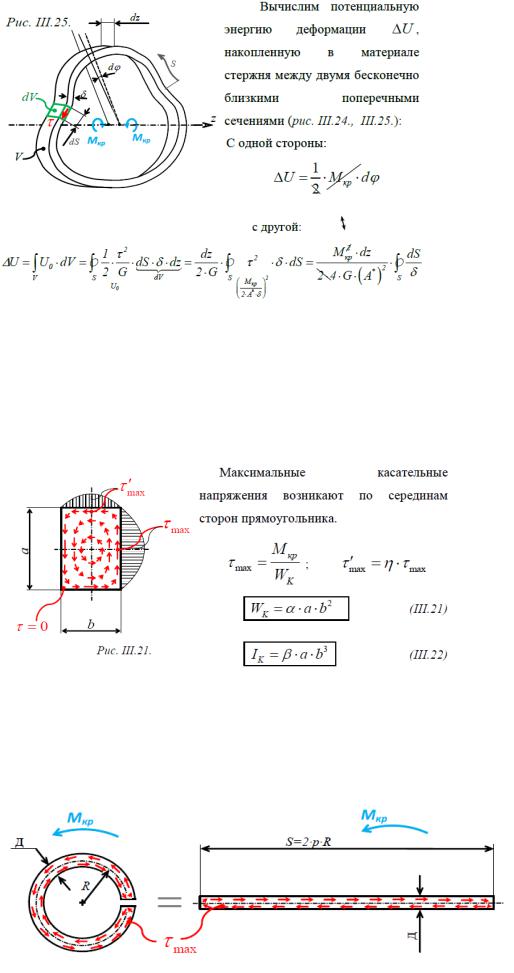
20.кручение стержня прямоугольного сечения: напряженное состояние особенностинапряженного состояния в угловых точках, распределение касат напряжений по попереч сечению, формулы для оперделения напряжений в точках располож в середени длинной и короткой стороны, формула для угла закручивания.

Распределение напряжений по поперечному сечению показывает

гидродинамическая аналогия и методы теории упругости:

Здесь b – всегда меньшая из сторон прямоугольника.

21.кручение гнутых тонкостенных открытых профилей: кручение длинной полосы(формула для мах касат напряжения, распределение касат напряжений по сечению, изменение касат напряжений по толщине полосы,формуля для угла закручивания)

Таким образом, если незамкнутый тонкостенный профиль может быть развернут в прямоугольник, то и его геометрические характеристики при кручении считаются также, как для прямоугольного профиля с соотношением сторон a/b =бесконечность.

Части составного тонкостенного профиля ведут себя при кручении, как самостоятельные прямоугольные профили, объединённые единственным условием: поворачиваются они, как жёсткое целое. Так, для профиля,изображённого на рис. III.28.: ф1=ф2=ф3=ф

Соответственно, внутренний крутящий момент всего сечения рассматривают, как сумму внутренних крутящих моментов в каждой части:

Здесь l – длина стержня рассматриваемого сечения.В общем случае для тонкостенного разомкнутого профиля,состоящего из i частей:

Доля внутреннего крутящего момента в i-й части открытого профиля

Максимальное касательное напряжение в i-й части открытого профиля

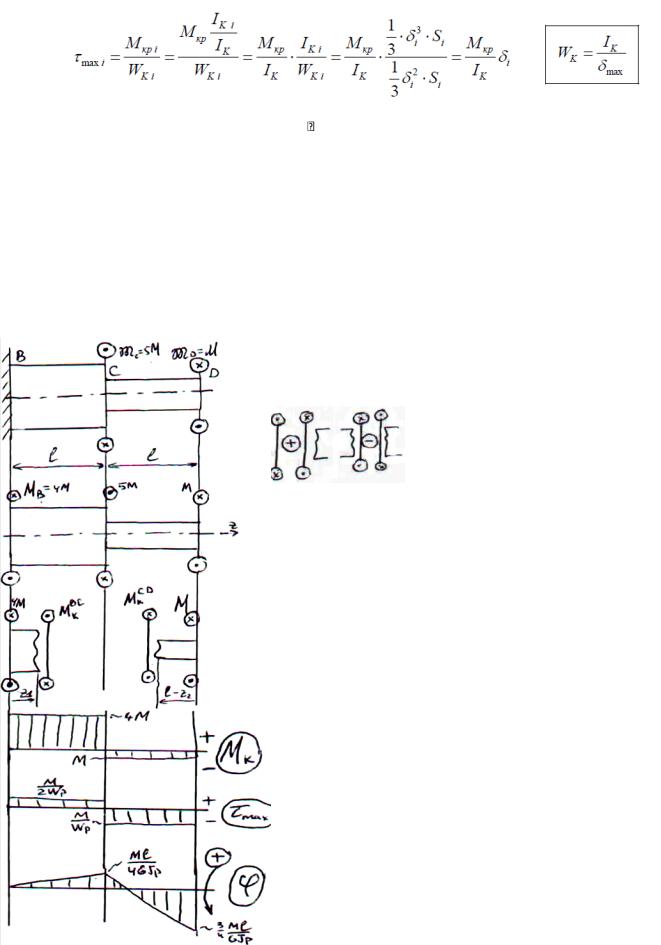
Видно, что наибольшее напряжение max в сечении тонкостенного разомкнутого профиля будет в участке с наибольшей толщиной

22=21

23.расчет на прочность при кручении: понятие о нормативном и расчетном коэф-те запаса,условие равнопрочности,расчет по допускаемым напряжениям.

Проведём расчёт на прочность на примере. Дано: М, , nТ, Построить эпюры Мк ,	, φ. Отбрасываем
заделку в сечении В-В. Внешние моменты обозначаются буквой

Выбираем направление Оz.Проверим систему на статическую опрлимость. Ус-вие равновесия: , - МВ + 5М - М=0. Отсюда МВ =4М → задача статич. определима. Для построения эпюры крутящих моментов Мк используем метод сечений и правило знаков:

Условие равновесия (если система находится в равновесии, то и каждая её часть находится в равновесии):

;

			1) -4М + С =0,	С = 4М;
2)	С + M = 0,	С	= -М
Определяем касательные напряжения по ф-ле:
		, где WP – полярный момент сопротивления.
Определяем углы поворота сечений по ф-ле:
		, где - полярный момент инерции сечения.
Опр-яем полярные моменты:					,
	,		,	С
Важно привести к общему знаменателю:
	,	С	. Строим эпюры.
При	расчёте	по	допускаемым напряжениям		используют	условие:
	, где			- макс. касательное напряжение,
	-допускаемое		кас.напряжение.	В целях	безопасной	работы

напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса): , где - предельное кас. напряжение материала, nТ – коэф. запаса, принимают [n] > nТ, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса. Таким образом:

. При проектировочном расчёте из полученного соотношения определяем d – диаметр поперечного сечения.

24.изменение моментов инерции плоской фигуры при параллельном переносе осей.

25.изменение моментов инерции плоской фигуры при повороте осей.

Найдём экстремум функции u I , то есть найдём такой угол , при
котором	Iu	достигает	своего	максимума	или	минимума:

Это тот же самый угол, при котором моменты инерции u I и Iv принимают экстремальные значения!Значит, для точки О на плоскости существует только одна пара координатных осей, относительно которых моменты инерции фигуры принимают экстремальные значения, а центробежный момент обращается в ноль. Эти оси называются главными.Если в точке плоскости задана некоторая система координат OXY и в ней подсчитаны моменты инерции фигуры , , x y xy I I I , то угол альфа0 между этой системой координат и главными осями вычисляется по формуле:

Какие именно экстремальные значения принимают моменты инерции вглавных осях, можно определить, в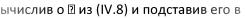

26=25

27.моменты инерции простейших фигур: вывод для круга прямоугольника,треугольника.

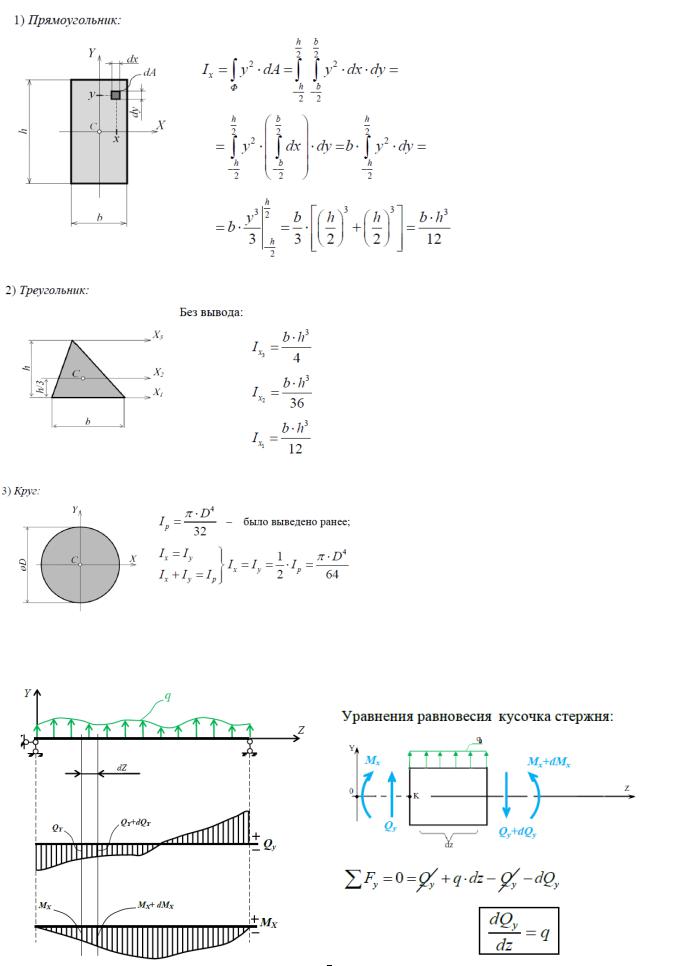
28.вывод диференциальной зависимости между интенсивностью внешней нагрузки q поперечной силой Qy и изгибающим моментом Mx.

29.вывод основных расчетных зависисотей при прямом чистом изгибе : определение чистого изгиба, определение прямого изгиба, определение нейтр слоя и линии, гипотезы связанные с напряженным состоянием при изгибе,связь напряжений с внутр силовыми факторами, связь деформаций с кривизной стержня, связь между кривизной и изгиб моментом, система осей ху является главной.

Чистый изгиб – изгиб, при котором изгибающий момент в сечении явл. единственным силовым фактором, а поперечные и нормальные силы отсутствуют. Чистый изгиб наз-ся прямым, если ориентация изгибающего момента совпадает с одной из главных осей поперечного сечения.

Рассмотри систему, изображённую на рис1. Брус находится в равновесии, имеем: 1)

; 2)

Т.к. рассматриваем чистый изгиб: (3) ; (4) ;

(5)

Из ур-ий 3) – 5) нельзя установить связь между моментом и напряжением => задача статич. неопределима=>необх. составить ур-ие перемещений. Образование деформаций при чистом изгибе можно рассматривать как р-тат поворота поперечн. сечений друг относ. друга. Рассмотрим два сечения, находящихся на расстоянии dz друг относ. друга (рис.2, 3).

	В р-тате поворота произвольно взятый отрезок MN=dz получает приращение					(M1N1-
	MN), кривизна	нейтрального слоя CD (в котором удлинения отсутствуют) изменяется
	(рис. 4):	→	.
	Относительное удлинение MN:
		(6)
		(6)→з-н Гука:		(7)
		(7)→(3):	,	,	=>	=> OX –
		нейтральная ось
		(7)→(4):		=> JXY = 0 => ОХ и ОY – главные центральные
		оси => изгиб прямой
(7)→(5):	.
=>	(8)
(8)→(7):
Макс. напряжение возникает в т.,			наиболее удалённых от нейтральной линии
(рис.5):	,

30.расчеты на прочность при изгибе: понятие о расчетном и нормативном коэф-те запаса,условие равнопрочности,расчет по допускаемым напряжениям.

По принципу независимости действия сил нормальное напряжение в произвольной точке, принадлежащей поперечному сечению бруса и имеющей координаты x, y, опр-ся суммой напр-й, обусловленных моментами

Mx и My , т.е. (x, y)	M x	y		M y x
					(5.26)
	I x
				I y

Mx = M sin ; My = M cos , где - угол между плоскостью главного мемента М и осью Ох или Оу. (5.25)

Правило знаков для моментов: момент считается положительным, если в первой четверти координатной плоскости (там, где координаты x и y обе положительны) он вызывает сжимающие напряжения.

Если изгиб чистый, то один из моментов Mx или My равен 0 и выражение (5.26) принимает вид

, где

- осевой момент сопротивления,

– осевой

момент инерции,

-

расстояние по модулю до наиболее удалённой точки сечения от Ох.

При косом изгибе МХ , МУ

.

Уравнение не йт р ал ь н о й

ли н ии , т.е. геометрического места

точек,

где

нормальное напряжение

принимает нулевые значения, находят, полагая в (5.26) = 0:

M x y

M y x

0

Откуда определяется: y

M y I x

x ctg

I x

x

(5.27)

I x

I y

M x I y

I y

Эпюра напряжений в поперечных сечениях бруса линейна, следовательно, максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии.

Расчёт на прочность при изгибе проводится при условиях:

1)	материал работает одинаково на растяжение и сжатие, т.е.						АС	С А
Условие прочности:				, где		,	, где	– допускаемое
значение предела текучести,				- коэф. запаса.
2)	если неодинаково, то работают два условия:
	АС	АС
			, где	АС	,	С	А
	С А			АС		С А

С А

Если расчёт проектировочный, то из двух коэффициентов выбирется наибольший. В поверочном – наоборот.

В целях безопасной работы напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса):

, где - предельное кас. напряжение материала, nТ – коэф. запаса,

за расчётный коэффициент принимают [n] > nТ, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса.