
7. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ САУ. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
7.1. Понятие об устойчивости САУ
На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.
Структурная схема замкнутой системы автоматического управления приведена на рис. 7.1, где x(t) – выходная величина; g(t) – задающее воздействие – возмущение, действующее на систему; W(p) – передаточная функция разомкнутой системы.
Рис. 7.1. Структурная схема САУ
Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.
Приведенное понятие устойчивости определяет устойчивость установившегося режима системы. Поэтому можно дать следующее, более общее определение устойчивости: система устойчива, если ее
выходная величина остается ограниченной в условиях действия на систему ограниченных по величине возмущений.
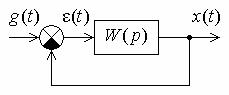
На рис. 7.2 показаны типичные кривые переходных процессов в неустойчивой (а) и устойчивой (б) системах при импульсных возмущениях.
141
а |
б |
Рис. 7.2. Переходные процессы при импульсных возмущениях:
а – в неустойчивой системе; б – в устойчивой системе
Наблюдения показывают, что некоторые положения равновесия системы устойчивы к небольшим возмущениям, а другие принципиально возможные равновесные положения практически не могут быть реализованы.
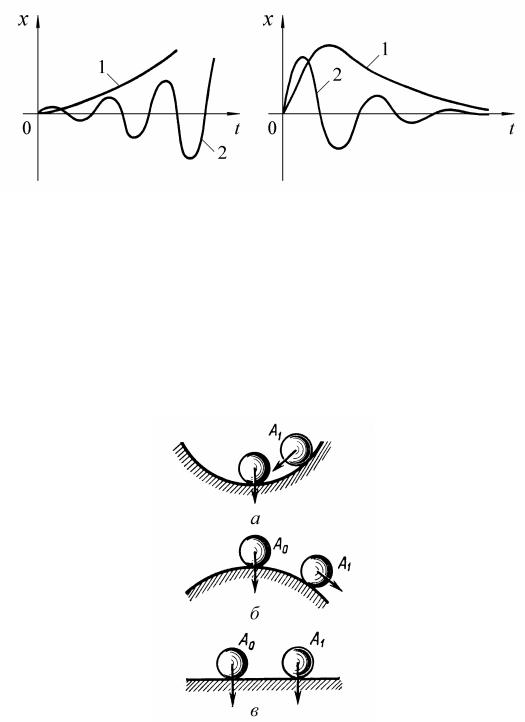
Рис. 7.3. К понятию об устойчивости САУ
Наглядно устойчивость равновесия представлена на рис. 7.3, где изображен шар, расположенный в некотором углублении (рис. 7.3, а), на некоторой выпуклой поверхности (рис. 7.3, б), на плоскости
(рис. 7.3, в).
Положение равновесия шара характеризуется точкой A0. В случае, изображенном на рис. 7.3, а, при всяком отклонении шара
142
от положения равновесия, например в точку A1, он будет стремиться снова возвратиться к положению равновесия – в точку A0 (при отсутствии сил трения). Такое положение равновесия (рис. 7.3, а) устойчиво. Случай, изображенный на рис. 7.3, б, соответствует неустойчивому положению равновесия. Рис. 7.3, в соответствует безразличному равновесию.
7.2.Исследования А. М. Ляпунова об устойчивости движения
7.2.1.Общая постановка задачи об устойчивости движения.
Впервые строгое определение устойчивости было дано русским ученым А. М. Ляпуновым в 1892 г. в работе «Общая задача об устойчивости движения». Отсутствие такого определения часто приводило к недоразумениям, так как движение, устойчивое в одном смысле, может оказаться неустойчивым при другом понимании этих слов, и наоборот. Определение устойчивости А. М. Ляпунова оказалось настолько удачным и наилучшим образом удовлетворяющим многим техническим задачам, что оно в настоящее время принято как основное.
Пусть движение системы автоматического управления описывается дифференциальными уравнениями, которые могут быть приведены к виду
dyi /dt Yi(y1, y2, , yn,t), |
(7.1) |
где yi – вещественные переменные, характеризующие |
состояние |
системы управления (обобщенные координаты); Yi – известные
функции переменных y1, y2,...,yn и времени |
t, удовлетворяющие |
||||
условиям существования и единственности решения. |
|
||||
Исходное |
состояние |
системы |
при |
t t0 |
однозначно |
определяется |
начальными |
значениями |
переменных |
yi, которые |
|
обозначим y10,y20,...,yn0. |
|
|
|
y10, y20,...,yn0 |
|
Каждой |
совокупности начальных значении |
||||
соответствует единственное решение (7.1) для всех t t0 |
|
||||
|
y y(y10, y20,...,yn0,t). |
|
(7.2) |
||
Решение (7.2) описывает какое-либо движение системы, определяемое исходным состоянием.
143
Некоторое вполне определенное движение системы, подлежащее исследованию на устойчивость, называют невозмущенным движением.
Заметим, что выбор невозмущенного движения является произвольным. Это может быть любое возможное движение системы, как установившееся, так и неустановившееся. Допустим, что в качестве невозмущенного движения выбрано такое, которое описывается заданными функциями времени
y |
y |
(t), y |
2 |
y |
(t),..., y |
n |
y |
(t). |
(7.3) |
1 |
1 |
|
2 |
|
n |
|
|
Предположим, что функции yi (t) являются частным решением дифференциальных уравнений (7.1), т. е.
|
dy |
/dt Y |
(y |
, y ,...,y |
,t), |
|
|
|
(7.4) |
||||||||
|
i |
|
|
|
|
i |
1 |
|
2 |
n |
|
|
|
|
|
||
удовлетворяющим начальным условиям при t t0 |
|
|
|
||||||||||||||
y |
y (t |
0 |
), y |
2 |
y |
(t |
0 |
),..., y |
n |
y |
(t |
0 |
). |
(7.5) |
|||
1 |
1 |
|
|
|
2 |
|
|
|
|
n |
|
|
|||||
В частном случае, когда параметры системы не изменяются со |
|||||||||||||||||
временем и функции Yi |
не зависят явно от t, движения (7.3) являются |
||||||||||||||||
установившимися. Им отвечают решения |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
y |
const, |
|
|
|
|
|
|
(7.6) |
|||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
служащие корнями уравнений |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Yi(y1, y2,...,yn) 0. |
|
|
|
|
|
|
(7.7) |
|||||||||
Изменим условия (7.5), дав начальным значениям переменных y1, y2,...,yn небольшие по модулю приращения ε1,ε2,...,εn т. е. пусть при t t0
y |
y (t |
0 |
) ε , y |
2 |
y |
(t |
0 |
) ε |
2 |
,..., y |
n |
y |
(t |
0 |
) ε |
n |
. |
(7.8) |
1 |
1 |
1 |
2 |
|
|
|
n |
|
|
|
|
Движение системы, отвечающее измененным начальным условиям (7.8), называют возмущенным движением. Другими словами, возмущенным движением системы называют всякое иное движение системы, отличное от невозмущенного.
Введем новые переменные
x |
y |
(t) y |
(t), |
(7.9) |
i |
i |
i |
|
|
равные разности переменных yi в возмущенном и невозмущенном движении. Переменные xi называют отклонениями или вариациями величин yi. Если все отклонения равны нулю
144
x1 0,x2 0,...,xn 0, |
(7.10) |
то возмущенное движение yi(t) будет совпадать с невозмущенным движением yi (t), т. е. невозмущенному движению отвечают нулевые значения переменных xi.
Пусть при t t0 переменные xi принимают какие-либо свои начальные значения xi0, из которых, по крайней мере, одно не равно нулю
|
xi xi0 εi. |
|
(7.11) |
|
Начальные |
значения |
отклонений |
(7.11) |
называют |
возмущениями.
А. М. Ляпуновым было дано следующее определение устойчивости. Невозмущенное движение называют устойчивым по отношению к переменным xi, если при всяком произвольно заданном положительном числе ε, как бы мало оно ни было, можно выбрать другое такое положительное число δ(ε), что при всяких возмущениях xi0, удовлетворяющих условию
n |
|
xi20 δ, |
(7.12) |
i1
ипри любом t t0 будет выполняться неравенство
n |
|
xi2(t) ε, |
(7.13) |
i1
впротивном случае движение неустойчиво.
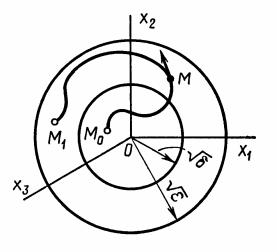
Геометрическая интерпретация |
определения |
устойчивости |
||||
приведена на рис. 7.4. Здесь совокупность отклонений |
x1,x2,...,xn |
|||||
в n-мерном |
пространстве определяет |
положение |
изображающей |
|||
точки M . |
В возмущенном движении при изменении величин |
|||||
x1,x2,...,xn |
изображающая точка будет описывать некоторую |
|||||
траекторию. |
Невозмущенному |
движению |
xi |
0 |
отвечает |
|
неподвижная точка – начало координат.
Практически устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения. Если же невозмущенное движение
145
неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.
Рис. 7.4
Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных
возмущениях стремится к невозмущенному движению, т. е. |
|
lim x (t) 0, |
(7.14) |
t i |
|
то невозмущенное движение называют асимптотически устойчивым. При асимптотической устойчивости изображающая точка с течением времени должна неограниченно стремиться к началу
координат, не выходя из сферы ε.
Отметим некоторые особенности определения устойчивости по А. М. Ляпунову. Во-первых, предполагают, что возмущения налагаются только на начальные условия, иначе говоря, возмущенное движение происходит при тех же силах (источниках энергии), что и невозмущенное движение. Во-вторых, устойчивость рассматривают на бесконечно большом промежутке времени. В-третьих, возмущения предполагаются малыми.
7.2.2. Теоремы А. М. Ляпунова об устойчивости движения по первому приближению. Когда известно общее решение
дифференциальных |
уравнений |
движения |
(7.1), |
можно |
||
непосредственно |
определить |
значения |
переменных |
yi(t) |
||
в возмущенном движении, составить вариации |
x |
y (t) y (t) |
||||
|
|
|
|
i |
i |
i |
146
и, исследуя их, решить вопрос об устойчивости невозмущенного движения yi (t).
Однако, как правило, исследование устойчивости движения производят не путем анализа общего решения, а с помощью методов, основанных на качественном анализе дифференциальных уравнений возмущенного движения, которым удовлетворяют отклонения (вариации) xi.
Чтобы вывести уравнения возмущенного движения, найдем из
(7.9) переменные |
y (t) y |
(t) x |
|
и подставим эти значения |
y (t) |
||||||
|
|
i |
i |
i |
|
|
|
|
|
|
i |
в дифференциальные уравнения движения (7.1). Тогда |
|
||||||||||
dy |
(t)/dt dx (t)/dt Y (y |
x , y x ,...,y |
|
x ,t). |
(7.15) |
||||||
|
i |
i |
|
i |
1 |
i |
2 |
i |
n |
i |
|
Если |
правые |
части |
уравнений (7.15) |
допускают разложение |
|||||||
в степенные ряды Тейлора, то после этого разложения по степеням xi получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dyi (t) |
|
dxi(t) |
|
|
|
|
|
|
Yi |
|
|||
|
|
|
|
|
|
|
|||||||
dt |
|
dt |
Yi(y1 |
, y2 |
,...,yn |
, ,t) |
x |
x1 ... |
|||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
Yi |
|
|
|
|
|
|
|
|||
|
|
|
|
|
xn Ri(x1,x2,...,xn), |
|
(7.16) |
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
xn 0 |
|
|
|
|
|
|
|
||
где Ri(x1,x2,...,xn) – совокупность членов, зависящих от отклонений xi в степени выше первой.
Учитывая (7.5), будем иметь
dxi(t)/dt ai1xi1 ai2xi2 ... ainxin Ri(x1,x2,...,xn). (7.17)
В (7.17) коэффициенты
|
|
Yi |
|
|
|
aik |
|
|
|
(7.18) |
|
|
|
||||
|
|
|
|
||
|
|
xk |
xk |
0 |
|
|
|
|
|
||
в общем случае являются функциями времени t; в частности, они могут быть постоянными. Будем считать их постоянными.
Уравнения (7.17) называют дифференциальными уравнениями возмущенного движения.
Если отклонения xi достаточно малы, то, пренебрегая Ri(x1,x2,...,xn), получим линеаризованные уравнения
dxi(t)/dt ai1x1 ai2x2 ... ainxn, |
i 1,2, ,n, |
(7.19) |
называемые уравнениями первого приближения.
147
Во многих случаях устойчивость движения исследуют по уравнениям первого приближения. Это объясняется не только простотой этого метода, но также и тем, что весьма часто наши знания процессов, происходящих в реальных системах, позволяют надежно определять только первые линейные члены. Однако уравнения первого приближения могут дать иногда совершенно неверное заключение об устойчивости движения. Поэтому, естественно, возникает вопрос об определении условий, при выполнении которых уравнения первого приближения дают правильные ответы об устойчивости движения. Эту исключительно важную и принципиальную для теории автоматического управления задачу впервые поставил и решил А. М. Ляпунов.
Системе уравнений (7.19) соответствует характеристическое уравнение, которое можно записать следующим образом:
|
a11 p |
a12 |
|
a1n |
|
|
|
D(p) |
a21 |
a22 p |
|
a2n |
0. |
(7.20) |
|
|
|
|
|
||||
|
|
|
|||||
|
an1 |
an2 |
ann p |
|
|
||
Из (7.20) можно найти его корни pi, где i 1,2, ,n, которые в общем случае имеют вид pi αi jωi , где αi и ωi – вещественные и мнимые части корней соответственно.
Для исследования устойчивости систем по их линеаризованным уравнениям принципиально важны следующие теоремы А. М. Ляпунова, которые приведем без доказательства.
Теорема 1. Если вещественные части всех корней pi характеристического уравнения (7.20) первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.
Теорема 2. Если среди корней pi характеристического уравнения (7.20) первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.
Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют критическим. Как показал Ляпунов, в критическом случае
148

устойчивость (неустойчивость) невозмущенного движения не может быть оценена по уравнениям первого приближения, так как она зависит от вида нелинейной функции Ri(x1,x2,...,xn), и поэтому в этом случае требуется рассмотрение дифференциальных уравнений возмущенного движения (7.17) в их исходном виде.
7.3. Необходимое и достаточное условие устойчивости САУ
Покажем, как на основе изложенного выше определения устойчивости А. М. Ляпунова можно найти условия устойчивости линейных (линеаризованных) систем автоматического управления.
Пусть для САУ, представленной на рис. 7.1, передаточная функция разомкнутой системы имеет вид
W(p) R(p), Q(p)
передаточная функция замкнутой системы
Ф(p) |
W(p) |
|
R(p) |
|
M(p) |
. |
|
Q(p) R(p) |
|
||||
1 W(p) |
|
|
D(p) |
|||
Тогда дифференциальное уравнение замкнутой системы
D(p)x(t) M(p)g(t).
Дифференциальное уравнение линейной системы автоматического управления, записанное для регулируемой выходной величины x(t) при наличии управляющего воздействия g(t), имеет вид:
(a |
pn a pn 1 ... a |
n |
)x(t) (b pm b pm 1 ... b )g(t), (7.21) |
||||
0 |
1 |
|
|
0 |
1 |
m |
|
где a0,a1, ,an |
и b0,b1, ,bm |
– |
постоянные |
коэффициенты, |
|||
а p d /dt – оператор дифференцирования. |
|
||||||
Изменение регулируемой величины x(t) при произвольном |
|||||||
внешнем воздействии g(t) |
представляет собой решение (7.21) |
||||||
|
|
|
x(t) xв(t) xсв(t). |
(7.22) |
|||
В (7.22) первое слагаемое xв(t) |
– вынужденная составляющая. |
||||||
Она определяется как частное решение неоднородного дифференциального уравнения (7.21) с правой частью.
(a0 pn a1pn 1 ... an)xв(t) (b0 pm b1pm 1 ... bm)g(t). (7.23)
149
Второе слагаемое xсв(t) – свободная (переходная) составляющая, которая определяется общим решением однородного дифференциального уравнения (7.21) без правой части
(a |
0 |
pn |
a pn 1 |
... a |
n |
)x |
св |
(t) 0. |
(7.24) |
|
|
1 |
|
|
|
|
|||
Обычно в теории |
автоматического |
управления |
интересуются |
||||||
устойчивостью вынужденной составляющей xв(t) переходного процесса. Поэтому за невозмущенное движение системы необходимо принять вынужденную составляющую переходного процесса xв(t). Тогда возмущенным движением будет любое возможное в системе изменение регулируемой величины x(t), а отклонением или вариацией будет свободная составляющая xсв(t) x(t) xв(t).
Возмущениями, по А. М. Ляпунову, являются начальные значения xсв, которые возникли в момент t t0 под действием внезапно подействовавших дополнительных внешних сил, т. е. начальные значения xсв0. Дифференциальными уравнениями возмущенного движения первого приближения в данном случае будут уравнения (7.24).
В соответствии с определением устойчивости по А. М. Ляпунову, система будет асимптотически устойчивой, если с течением
времени при t свободная составляющая |
будет стремиться к |
||||||||||
нулю, т. е. xсв(t) 0. |
Чтобы найти эту составляющую, |
необходимо |
|||||||||
решить дифференциальное уравнение (7.25) |
|
|
|
|
|
||||||
a |
|
dnxсв(t) |
a |
dn 1xсв(t) |
... a |
n |
x |
|
(t) 0. |
(7.25) |
|
|
|
|
|
||||||||
|
0 |
dtn |
1 |
dtn 1 |
|
св |
|
|
|||
Решение уравнения (7.25) при отсутствии кратных корней имеет |
|||||||||||
вид |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
xсв(t) Ciepit , |
|
|
|
|
(7.26) |
||
i 1
где n – порядок уравнения системы; Сi – постоянные интегрирования, определяемые из начальных условий; pi – корни характеристического уравнения
D(p) a |
pn a pn 1 |
... a |
n |
0, |
(7.27) |
0 |
1 |
|
|
|
150
