Основы физической оптики

81

Отсюда находим

:

r

= -

e

( w )

1

+ к.с.

(4.5).

E

r

m

w02

- 2igw - w2

Дипольный момент атома

= -e ×

и, если в единице объема концентрация

p

r

электронов равна N, то вектор поляризации

,

P

определяемый как дипольный

момент единицы объема, равен:

= Ner

(4.6),

или

P

= N

e2

×

1

×

( w)e−iωt + к.с.

(4.7).

P

E

m

w02 - 2igw - w2

Введем обозначение

k( w ) =

Ne2

×

1

(4.8).

e0 m

w2 - 2igw - w2

Тогда:

P = e0 k( w )E( w ) × exp( -iwt ) + c.c.

(4.9).

Из (4.9) видим, что наведенная поляризация действительно пропорциональна амплитуде внешнего электрического поля и имеет ту же частоту. Для выявления характера частотной зависимости параметров световых волн начнем с уравнений Максвелла:

rotH = ¶D + d ¶t

rotE = - ∂ ( mH ),

¶t

где

D = e0 E + P = e0 (1+ k )E = eE P = e0 kE

Первое из уравнений перепишем в виде:

rotH = sE + ∂ ( eE )

¶t

Считая среду непроводящей и немагнитной (s=0; m=m0), получим волновое уравнение обычным способом:

¶

¶

¶

rot rot

= -m

rot

= -m

×

D

E

H

¶t

0

¶t

0 ¶t

= -m0 ¶2

grad div

-

2

D

или

E

Ñ

E

¶t 2

= 0 , то данное уравнение запишется в форме:

и, поскольку divE

2 E - m0 ¶2

= 0

D

(4.10).

Ñ

¶t 2

Участок кривой вблизи

n

( )

N( )

82

Полагаем, что гармоническая световая волна распространяется вдоль она плоская и однородная (¶/¶x = ¶/¶y = 0). Волновое уравнение в случае принимает вид:

	¶2			¶2
		E	- m0e		E	= 0
	¶z 2			¶t 2

z и что таком

(4.11).

Подставляем в (4.11) решение в виде плоской волны, бегущей вдоль оси z: E( z,t ) = E0 × exp[ i( wt - kz )] , после чего приходим к соотношению:

- k 2 E + m0ew2 E = 0

Далее, учитывая, что

k =

ω

=

ω

× n , получим: m0ew

2

=

w2

n

2

или

n

2

v

c

c2

Итак, имеем для n2 соотношение:

	n2 = 1 +	Ne2	×	1
		m		w02 - igw - w2

	(4.12).
= m0 ec2 =	μ0ε0 ( 1 + κ ) = ( 1 + k ) .
	m0e0
	(4.13).

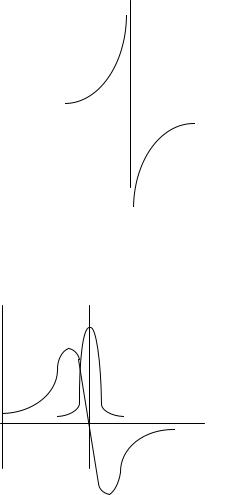
Очевидно, что в случае отсутствия потерь (g = 0) показатель преломления является вещественным. Его частотная зависимость представляет собой

разрывную функцию (разрыв при w=w0) (рис. 4.1).
			В случае, когда g ¹ 0,				n	становится
			комплексной	величиной.		Вид		частотных
			зависимостей	действительной				и	мнимой
			частей представлен на рис. 4.2. Здесь
			сплошной линией		отмечена		зависимость
			действительной части n(w), а пунктиром -
			зависимость	мнимой части.				Ясно, что
			мнимая часть n указывает на величину
			потерь на поглощение. Эти потери
		Рис. 4.1.	максимальны	при	w = w0.			Области,
			соответствующие частотам			w < w0,			w > w0

составляют область нормальной дисперсии. w0 с отрицательным наклоном кривой n(w) соответствует области аномальной дисперсии.

Большинство материалов, естественно, имеет несколько частот собственных колебаний w0n и, следовательно, несколько линий поглощения и областей аномальной дисперсии показателя преломления.

Рис. 4.2.

(4.14).

Это справедливо

что в пределе

83

Кривые дисперсии (зависимости n(ω)) всегда имеют характерный вид. В промежутке между двумя линиями поглощения тангенс угла наклона кривой дисперсии всегда положителен.

У высокочастотной границы этого промежутка величина показателя преломления самая высокая. При уменьшении частоты она сначала резко уменьшается, затем скорость спада существенно уменьшается. При достижении следующей полосы поглощения величина n опять резко уменьшается. Внутри полосы поглощения наклон кривой скачком изменяется на обратный. Это соответствует аномальной дисперсии. Величина n в этой области резко возрастает. На низкочастотном крае полосы поглощения наклон кривой n(ω) опять становится положительным. И т.д.

Используя последнее соотношение (4.13), легко видеть, низких частот (ω→0) величина n > 1:

n2 = 1 + Ne2

mω02

При очень высоких частотах (ω>>ω0) величина n → 1.

практически для всех веществ. Физическая причина такого поведения − инерционность электрона. При очень высоких частотах электрон (в одноэектронной модели атома) не успевает за внешним полем, поэтому дипольный момент атома p незначителен и при ω → ∞ p → 0.

Итак, как следует из рис. 4.2, зависимость n(ω) наиболее сильна вблизи резонансных частот, когда частота светового поля совпадает или достаточно близка к собственной частоте колебаний атомов или молекул. Это значит, что дисперсия показателя преломления наиболее сильна вблизи максимумов поглощения среды. Уже из этого факта вытекает, что между вещественной и мнимой частями показателя преломления существует сильная связь. Она имеет глубокую физическую основу и может быть выражена из принципа причинности. Соответствующее соотношение называют соотношением Крамерса – Кронига:

	2	∞		′
n( ω ) − 1 =		∫	ω				′ ′	(4.15).
	π		′	2
					− ω	2 κ( ω )dω
		0	( ω )

Это соотношение носит фундаментальный характер. Оно показывает, что величина n(ω) полностью определяется зависимостью κ( ω ) и наоборот.

4.2. Распространение света в направляющих структурах

Как известно, узкий световой пучок не может распространяться в однородной среде без изменения своего поперечного размера вследствие дифракции. Сохранение профиля пучка возможно при распространении света в направляющих структурах – волоконных, канальных и планарных оптических волноводах. Эффект направления световой энергии в таких

84

волноводах основан на явлении полного внутреннего отражения света на границе раздела диэлектрических сред. Первые работы по диэлектрическим оптическим волноводам выполнены в конце 60-х годов прошлого столетия. В настоящее время в этой области, включающей волоконную и интегральную оптику, выполнен огромный объем исследований и реализован целый ряд идей по созданию как отдельных функциональных элементов, так и более сложных интегрально – оптических схем для целей оптической обработки информации и оптической связи [3, 11].

В данном подразделе рассматриваются элементы электромагнитной теории планарного оптического волновода, являющегося базовым компонентом интегральной оптики, и кратко обсуждаются основные типы волноводно – оптических структур.

4.2.1. Электромагнитная теория планарного волновода

Рассмотрим планарный диэлектрический волновод, представляющий собой трехслойную структуру с размерами, не ограниченными в поперечных

X	Y		направлениях. Средний слой с
			толщиной h имеет более высокий
0	n1	Z	показатель преломления, в сравнении
	n0		с двумя другими слоями (рис. 4.3).
			Примером		подобных		волноводов
	θ		служит	диэлектрическая			пленка	с
Рис. 4.3. Планарный волновод			высоким	показателем		преломления,
-h	n2		нанесенная на подложку с более
			низким	показателем		преломления
			(например,		пленка	Ta2O5		на
			стеклянной подложке).
	Проведем анализ	планарного	оптического		волновода,		используя

волновой подход [3, 11]. Рассмотрим наиболее простой случай, соответствующий изотропной и непроводящей среде в пределах каждой из отдельных областей структуры. Считаем, что свет распространяется в направлении оси z, а в направлении оси y световое поле является однородным. Показатели преломления в пределах слоев структуры удовлетворяют соотношению: n2 < n1 < n0 . Ищем поле направляемых волн в виде:

		( x, z ) =		m ( x ) × exp[ i( wt - bz )]	(4.16),
	E		E

где b – постоянная распространения. Здесь световое поле представлено в виде неоднородной плоской волны. При анализе будем исходить из уравнений Максвелла:

85

∂

D

rotH =

∂t

(4.17),

= − ∂B

rotE

подразумевая, что ρ = 0 ;

∂t

= 0 .

d

Учтем, что

= e ×

= m

, тогда в декартовой системе координат

D

E

и

B

H

эти уравнения принимают вид:

¶H

z

-

∂H y

= e

¶E

x

¶E

z

-

∂Ey

= -m

¶H

x

¶y

¶z

¶t

¶z

¶t

¶y

¶H x

-

¶H z

= e

∂Ey

¶Ex -

¶Ez = -m

∂H y

¶z

¶x

¶t

¶z

¶x

¶t

∂H y

-

¶H

x = e

¶E

z

∂Ey

-

∂Ex

= -m

∂H

z

¶x

¶y

¶t

¶x

¶y

¶t

Далее, учтем, что при заданном виде поля операция дифференцирования по времени эквивалентна умножению соответствующей компоненты на iω, а

операция

дифференцирования

по z эквивалентна ее умножению

на − iβ .

Учтем также, что

∂

¶y

= 0 , тогда получим:

βH y

= ωεEx

βEy = −ωμH x

- ibH x - ∂H z

- ¶

z

= iweEy

- ibEx

E

= -iwmH y

(4.18).

∂H y

¶x

∂Ey

¶x

= iweEz

= -iwmH z

¶x

¶x

Видим, что все эти уравнения делятся на две независимых системы:

∂H z

βH

= ωεE

− iβH x −

= iωεEy

y

x

∂x

∂H y

1)

βEy

= −ωμH x

2)

= iωεEz

(4.19)

∂x

∂Ey

= −iωμH

∂Ez

∂x

z

iβEx +

∂x

= iωμH y

Первая система связывает компоненты поля Ey, Hx и Hz, а вторая

система –

компоненты Hy, Ex,

Ez. Это поперечно – электрические или ТЕ и

поперечно

– магнитные или

ТМ волны. Им

соответствуют ориентации

векторов поля в световой волне внутри слоя, показанные на рис. 4.4.

86

	H	Y		E	Y
X	E	n2	X	H	n2
		Z			Z
	k	n0		k	n0
		n1			n1

Рис. 4.4. Расположение векторов E и H в TE волне (слева) и в TM волне (справа).

Обратим внимание на следующие 2 уравнения из систем (1) и (2):

∂Ey

= -iwmH z и

∂H y

= iweEz

(4.19).

¶x

¶x

Их можно записать в форме:

∂Ey

∂Ey

H z

= -

1

=

i

(4.20)

iwm

¶x

wm ¶x

и

Ez

=

1

∂H y

= -

i

∂H y

(4.21).

iwe

¶x

we

¶x

Далее эти соотношения понадобятся при записи граничных условий, необходимых для получения дисперсионного уравнения волновода.

Как можно видеть, системы (4.17) являются замкнутыми, т.е. они позволяют получить соответствующие уравнения (волновые уравнения) для каждой из компонент поля. Так, подставляя в первое уравнение системы(4.17) выражения для Hx и Hz , получим:

b

¶ i

¶Ey

- ib

-

E

-

= iweE

или

wm

y

¶x wm ¶x

y

b2

E

-

1

¶2 Ey

- weE

= 0

или

wm

y

wm

¶x2

y

¶2 E

y

- b2 Ey + w2emEy = 0 ,

¶x2

но w2 em = k 2 , поэтому окончательно волновое уравнение для компоненты Ey принимает вид:

¶2 Ey	+ (k 2	- b2 )× Ey = 0	(4.22).
¶x2

Аналогично получим:

87

iβ

β

+

∂

−

i

∂H y

− iωμ H y

= 0

или

H y

ωε

∂x

ωε

∂x

β2

1 ∂

1

∂H y

H y −

− ωμH y

= 0

ωε

ε

∂x

ω ∂x

Однако величину (1/ε) мы в общем случае не можем вынести из под знака дифференцирования, поскольку ε может меняться скачком (в рассматриваемом случае) на границах раздела x=0 и x=- h, или непрерывно в пределах световодного слоя в градиентных волноводах.

¶

1 ¶H y

¶ 1

¶H y

1 ¶2 H y

Т.е.

=

×

+

¶x

¶x

e

x2

e ¶x

¶x e

¶

Тогда:

∂

1 ∂Η y

1

∂ 2Η y

β2Η y − ε

+

− ω2μεΗ y

= 0

∂x

ε

∂x 2

∂x

ε

В пределах каждого из слоев поле описывается уравнением:

∂2 H y	+ (k 2	− β2 )H = 0
∂x2		y

(4.23).

(4.24)

(4.25).

Подобным же образом можно получить и другие волновые уравнения из системы (4.17) для компонент, например, Hz и Ez.

Решения волновых уравнений.

Получим решения для волнового уравнения (4.21), т.е. для ТЕ-мод. Вид распределений Ey(x) определяется решением уравнения:

	∂2 E	y	+ ( k		2	− β2 )E = 0 ,
	∂x2
						y
где k = nk						– волновое число света в среде; k =		2π	– волновое число в
				0				λ
							0

вакууме; n – показатель преломления среды. В случае, когда выполняется условие полного внутреннего отражения для световой волны в центральном

слое с показателем преломления n , величина ( k 2	− β2 ) > 0 для этого слоя,
0
но ( k 2 − β2 ) < 0 для прилегающих сред.

Действительно, k = k0 n0 при 0 > x >-h и k = n1k0 при x <-h ; k = n2k0 - при x > 0. С другой стороны β = n0 k0 sin θ и если θ > θkp , то n0 sin θ > n1 ,n2 . Соответственно, (k0 n0 )2 − β2 > 0 ,

(k0 n1 )2 − β2 < 0 , (k0 n2 )2 − β2 < 0 .

88

Таким образом, решения волнового уравнения (4.21) для различных областей структуры имеют вид:

a) Волноводный слой (n=n0):

Ey (x) = A1 exp[iκx]+ A2 exp[− iκx]

(4.26),

где κ =

.

( k

n )2

− β2

0

0

б) Подложка и покровный слой (n= n1 ,n2 ):

Ey (x) = B1 exp[iγ1,2 x]+ B2 exp[− iγ1,2 x]

(4.27),

где g

1,2

=

b2 - k

2n2 .

0

1,2

Из условий конечности поля

Ey (± ∞) следует:

E

y

(x)(1)

: E

y

(- ¥)(1)

= 0 ® B

(1) = 0

2

E

y

(x)(2 ) : E

y

(¥)(2 ) = 0 ® B(2 )

= 0

1

Таким образом, окончательно имеем:

Ey(2 )(x) = B × exp(- g2 x)

E

(0 )(x) = A × exp(ikx) + A × exp(- ikx)

(4.28).

y

1

2

(1)

= C × exp[g1 (x + h)]

Ey

Аналогичные соотношения можно получить и для ТМ волн.

Для конкретизации распределений полей мы должны определить соотношения между постоянными А, В, С, что может быть сделано с использованием граничных условий.

4.2.2. Дисперсионное уравнение планарного волновода

Граничные условия позволяют получить дисперсионное уравнение, связывающее характеристики волноводных мод с частотой и параметрами направляющей структуры.

Исходим из соотношений (4.27) и стандартных граничных условий для

тангенциальных компонент векторов E и H при x=0 и x= –		h:
Ey(0 )(0) = Ey(2 )(0)	H z(0 ) = H z(2 ) (0)
Ey(0 )(- h) = Ey(1)(- h)	H z(0 )(- h) = H z(1)(- h)	(4.29)

C учетом соотношения (4.18), выражения для H z заменим на аналогичные

∂Ey

соотношения для ¶x . Из (4.28) имеем:

89

Ey(2)(0) = B

E0y ( 0 ) = A1 + A2

Ey(0 )(- h) = A1 exp(- ikh) + A2 exp(ikh)

Ey(1)(- h) = C

¶Ey(2 )

¶x

¶Ey(0 )

¶x

¶Ey(1)

¶x

= -g2	¶Ey(0 )			= ikA1 - ikA2
	¶x
x=0				x=0

= ikA1 exp(- ikh) - ikA2 exp(ikh)

x = −h

= -g1C

x = −h

Для упрощения запишем распределения полей (13) в виде :

Ey(2)(x) = B × exp(- g2 x)

E	(0 )(x ) = A	1	× cos (kx ) + A	2	× sin (kx )	(4.30)
	y

Ey(1)(x) = C exp[g1 (x + h)]

И тогда:

Ey(2 )(0) = B

Ey(0 ) (0) = A1

Ey(1)(- h) = C

¶Ey(2 )			= -g	2
¶x
			x =0

¶E (0 )

y = kA ¶x 2

x =0

¶Ey(0 ) = kA1 × sin(kh) + kA2 × cos(kh)

¶x

x = −h

¶Ey(1)			= -g	1C
¶x
			x = −h

В итоге получим:

1) B = A1

2) - g2 B = kA2 ® A2 = - γk2 × B

3) A1 × cos(kh)- A2 × sin(kh) = C

4) κA1 sin(κh) + κA2 cos(κh) = γ1C

Выразим все коэффициенты через В.

90

Выражение для полей с учетом найденных коэффициентов:

Ey(2 )(x) = B exp(- g2 x)

E	(0 )(x ) = B		cos	κh −			γ 2	sin (κx )			(4.31).
	y						κ
E	(1)(x) = B	cos kh +			g2	sin(kh) exp[g				1	(x + h)]E
	y				k

Однако в этих выражениях не определены величины k, g1, g2 , которые зависят от угла θ или от постоянной распространения b. Их можно определить, используя оставшееся соотношение 4):

4) κA1 sin(κh) + κA2 cos(κh) = γ1C

A = B ; A = -				γ2		× B
				k
1	2
C = B cos(κh) +		γ2			B sin(κh) = B		cos(κh) +	γ2	sin(κh)
			κ					κ

C учетом этих соотношений мы можем переписать выражения (4.31) для поперечного распределения полей в пределах каждого из слоев

структуры.

А из 4) найдем дисперсионное уравнение:

γ

γ

2

= cos(κh)[γ1 + γ2 ] или

sin(κh) κ −

1

κ

γ1

γ2

tg(κh) =

ϑ1 + ϑ2

+

=

κ

κ

κ − ϑ1ϑ2

1 −

γ1γ2

κ2

κ

Сравнивая это выражение с известным соотношением из тригонометрии

	tg(α + β) =	tgα + tgβ	, придем к соотношению:
		1 − tgαtgβ
				γ	1
	κh = α + β , где α = arctg
				κ

β = arctg γ2κ

Или, с учетом периодичности функции tg,

		γ	1			γ	2
	κh = arctg				+ arctg				+ πm	(4.32).
		κ				κ

Это и есть дисперсионное уравнение планарного диэлектрического волновода. Запишем его в несколько другом виде, учитывая что:

κ = (k0 n0 )2 − β2 = k0 n02 − n02 sin2 θ

n0 sin θ = Nm -эффективный показатель преломления.