4. Приближённые методы решения уравнения Шрёдингера.
4.1. Стационарная теория возмущений для дискретного невырожденного спектра.
Постановка задачи.
4.1. Стационарная теория возмущений для дискретного невырожденного спектра. Постановки задачи.
Точное аналитическое решение уравнения Шредингера можно найти только для очень небольшого числа задач. Одним из приближенных методов решения уравнения Шредингера является метод теории возмущений.
Этот метод удобно применять тогда, когда рассматриваемая физическая система незначительно отличается от другой физической системы, для которой известно аналитическое решение уравнения Шредингера.
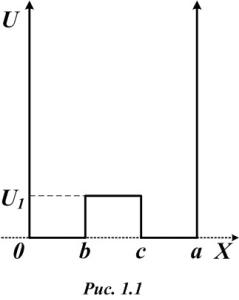
Мы в качестве примера системы, допускающей решение методом теории возмущений, рассмотрим бесконечную потенциальную яму (яму со стремящимися к бесконечности стенками), на дне которой потенциальная
энергия U ≠ 0. |
|
, |
x 0 |
|
Один из возможных |
||||
примеров |
такой |
|
|
|
0, |
0 x b |
|||
потенциальной |
ямы |
|||
изображен на рисунке. |
|
|
||
|
, b x c |
|||
|
|
U U1 |
||
|
|
0, |
c x a |
|
|
|
|
|
|
|
|
|
x a |
|
|
|
, |
||
|
|
|
|
|
4.1. Стационарная теория возмущений для дискретного невырожденного спектра. Постановки задачи.
Требуется определить собственные значения энергии частицы массы m в такой «потенциальной яме», а также волновые функции, соответствующие этим собственным значениям.
Пусть гамильтониан системы можно представить в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H H0 |
V, |
|
|
|||
где |
|
гамильтониан, |
|
собственные |
функции и |
|||||
H0 |
|
|||||||||
собственные |
значения |
которого |
известны, |
а |
малая |
|||||
|
|
|
|
|
|
|
|
|
V |
|
добавка к гамильтониану |
H0. |
|
|
|
|
|||||
|
- «невозмущённый» оператор Гамильтона, |
|
||||||||
H0 |
|
|||||||||
|
«оператор возмущения». |
|
|
|
|
|
||||
V |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
Гамильтониан |
H H0 V, |
|
будем называть возмущённым. |
|||||||
Собственные значения энергии и собственные функции гамильтониана H0 определяется стационарным уравнением Шредингера
H 0 (x).
4.1. Стационарная теория возмущений для дискретного невырожденного спектра. Постановки задачи.
H 0 (x).
Все решения этого уравнения известны, то есть известен набор собственных функций { i} и соответствующих этим собственным функциям собственных значений { i} .
Будем рассматривать случай дискретного невырожденного спектра
собственных значений { i}.
Будем также считать, что оператор возмущения можно представить в виде
|
|
|
V W, |
|
|
где λ - малый безразмерный параметр, |
|
- некоторый (не малый) оператор. |
W |
||
Теперь задача сводится к решению уравнения
H0 W E .
4.2. Стационарная теория возмущений для дискретного невырожденного спектра.
Основные уравнения.
4.2.Стационарная теория возмущений для дискретного невырожденного спектра. Основные уравнения.
Итак, задача сводится к решению уравнения
|
|
|
|
|
|
|
|
||
|
H 0 |
W x E x . |
||
|
|
|
|
|
Оператор H0 |
является эрмитовым оператором, а собственные функции всякого |
|||
эрмитова оператора образуют полный ортонормированный набор функций, то есть они могут служить базисом некоторого пространства. Это значит, что любую функцию, в том числе и волновую функцию можно представить в виде разложения по этому базису
(x) an n (x),
где i x - собственные функцииn гамильтониана H0 .
Подставим волновую функцию, записанную в таком виде, в уравнение Шрёдингера:
|
|
|
|
an n (x) Ek an n (x). |
|
|
|
||||
H0 |
W |
||||
|
|
|
|
n |
n |
4.2.Стационарная теория возмущений для дискретного невырожденного спектра. Основные уравнения.
|
|
|
|
an n (x) Ek an n (x). |
|
|
|
||||
H0 |
W |
||||
|
|
|
|
n |
n |
Подействуем оператором в левой части на волновую функцию.
|
|
|
|
|
|
|
|
|
|
an n (x) Ek an n (x). |
|
|
||||||||||||
|
|
H0 an n |
(x) W |
|
|
|||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
Умножим последнее уравнение на |
m (x) слева и проинтегрируем по всей |
|||||||||||||||||||||||
области определения волновых функций : |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
0 n n |
|
|
m |
|
|
|
n n |
|
|
|
k m |
|
|
n n |
|
||||||||
m |
|
|
|
|
|
|
|
|
(x) |
(x)dx. |
||||||||||||||
(x) H |
|
|
a |
(x)dx (x) W |
|
a |
(x)dx E |
|
|
a |
||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
Вычисляем интегралы в последнем уравнении. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
I |
|
|
|
|
|
a |
(x)dx |
a |
(x) |
|
|
|
(x)dx |
|
|
|||||||||
|
(x) H |
H |
|
|
||||||||||||||||||||
1 |
|
|
m |
|
0 |
n n |
|
|
|
|
n m |
|
|
0 |
n |
|
|
|
|
|
|
|||
n m |
|
|
|
n |
|
|
n m |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
n n |
|
n |
n |
|
|
a |
|
am m . |
||||||||||||||||
a |
|
(x) |
|
(x)dx |
a |
|
(x) |
(x)dx |
|
|
||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
n |
|
n n mn |
|
|
|
|
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.2. Стационарная теория возмущений для дискретного невырожденного спектра. Основные уравнения.
Второй интеграл |
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|||||||
|
|
|
|
|
I |
2 |
|
m |
|
(x)dx. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
(x) W |
|
a |
|
|
|
|||||||||
|
|
|
2 |
|
m |
|
|
|
n n |
|
|
|
|
|
n m |
|
n |
|
||
|
|
I |
|
|
|
|
(x)dx |
|
a |
|
(x)dx |
|||||||||
|
|
|
(x) W |
|
a |
|
|
|
(x)W |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
Третий интеграл (из правой части уравнения): |
|
|
|
|
|
|
|
|||||||||||||
I |
3 |
E |
(x) |
a |
(x) E |
a |
(x) |
|
(x)dx |
|||||||||||
|
|
|
|
k m |
|
|
n n |
|
|
k n m |
n |
|
|
|||||||
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
Ek an mn Ek am. n
Подставим полученные выражения для интегралов в уравнение.
|
0 |
n n |
|
|
|
|
|
n n |
|
|
k m |
n n |
|
|
m |
|
|
m |
|
(x)dx E |
(x)dx. |
||||||||
(x) H |
|
a |
(x)dx (x) W |
a |
|
(x) |
a |
|||||||
|
|
n |
|
|
|
|
|
|
|
|
(x)dx E a |
n |
|
|
|
|
a |
m |
|
a |
(x)W |
n |
|
|
|||||
|
|
|
m |
|
n m |
|
|
|
k m |
|
|
|||
n
4.2.Стационарная теория возмущений для дискретного невырожденного спектра. Основные уравнения.
a |
m |
|
|
a |
|
(x)W |
n |
(x)dx E a |
||
m |
|
n m |
|
k m |
||||||
|
|
|
n |
|
|
|
|
|
|
|
Обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
(x)W |
|
(x)dx. |
|||
|
|
|
|
|
||||||
|
|
mn |
|
m |
|
n |
|
|
||
Величины Wmn назовём матричными элементами возмущения.
Теперь
am m anWmn Ek am. n
Вместо исходного уравнения
|
|
|
|
|
|
||
H 0 |
W x E x |
||
|
|
|
|
мы получили систему алгебраических уравнений относительно коэффициентов {an}. Если нам удастся решить эту систему уравнений и найти коэффициенты
{an}, то волновую функцию можно будет записать в виде
(x) an n (x).
n
4.2.Стационарная теория возмущений для дискретного невырожденного спектра. Основные уравнения.
am m anWmn Ek am.
Эта система уравнений является nточным аналогом исходного уравнения Шрёдингера, даже без учёта малости параметра λ.
Для наглядности запишем её для случая m = 3 и для собственного значения
энергии Ek. |
a |
|
aW a W |
a W |
|
E a |
||||||||||||||
|
1 1 |
|
|
|
1 11 |
2 12 |
3 13 |
|
k |
|
1 |
|||||||||
|
a |
2 |
a W a W a W |
|
E a |
|||||||||||||||
|
2 |
|
|
|
1 21 |
2 22 |
3 23 |
|
k |
2 |
||||||||||
|
a |
|
|
|
aW a W a W |
|
E |
a |
||||||||||||
|
3 3 |
|
|
1 31 |
2 32 |
3 33 |
|
k |
|
3 |
||||||||||
|
a W a W a W a |
|
|
Ek 1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
11 |
|
2 |
12 |
3 |
13 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
a1W21 a2W22 a3W23 a2 |
|
k |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aW a W a W a |
Ek 3 |
|
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
1 |
|
31 |
|
2 |
32 |
3 |
33 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|