Результирующее выражение для tдов равно:

tдов = tдов1(1 Pзапр) +tдов2Pзапр r 1;

где r 1 — среднее число повторений кодовых комбинаций.

3.3.4. Расчет емкости накопителя-повторителя

Для расчета емкости накопителя-повторителя по временной диаграмме рис. 3.4 определим значения времени повторения: Tповт = hnt0.

Tповт — это то время, в течение которого в канале связи передается повторяемая по запросу информация из накопителя-повторителя. Из рис. 3.4 видно, что это время включает два цикла tp + nt0 +ta.

1.Первый цикл — прием комбинаций с обнаруженной ошибкой (ось «прием станции Б»).

2.Второй цикл — прием комбинации «запрос» (ось «прием станции А»), а также интервал (ось «передачи станции А»).

Таким образом:

Tповт = hnt0 = 2 (tp + nt0 +ta) + DT:

В синхронной системе временной интервал DT может иметь следующее значение:

0 DT nt0:

Примем DT = nt0, значит, hnt0 3nt0 + 2(tp +ta), откуда находим

h 3 + 2(tp +ta): nt0

3.4.Рекомендации по выбору оптимального кода

3.4.1.Расчет оптимальных характеристик помехоустойчивого кода

При выборе помехоустойчивого кода используется критерий максимума скорости передачи. По этому критерию оптимальным считается такой код, применение которого в системе с решающей обратной связью обеспечивает заданные требования по достоверности и максимальное значение скорости передачи системы. Код будет оптимальным, если

Pош(l) Pдоп(l) и R = Rmax;

где Pдоп(l) — допустимое значение вероятности ошибочного приема l-эле- ментной комбинации первичного кода; Pош(l) — значение вероятности ошибочного приема l-элементной комбинации первичного кода, получаемое при использовании в системе РОС-ППбл помехоустойчивого кода.

89

Ранее была получена формула для оценки вероятности Pош(C) ошибочного приема используемых в РОС-ППбл комбинаций помехоустойчивого (n;k)-кода.

Получим формулу для расчета Pош(l).

В приемник сообщения поступают те ошибки, которые не обнаружены декодером, т. е. только те образцы ошибок, вид которых совпал с видом разрешенных комбинаций. Эти образцы ошибок в составе n-элементных комбинаций имели вес от d и более. Естественно, что в составе блоков, выдаваемых в приемник сообщений, будут исключены ошибки, приходящиеся на избыточные разряды. Будем также считать, что числом и вероятностью ошибок кратности до d 1 в информационных блоках, оставшихся после удаления избыточных разрядов, можно пренебречь по сравнению с числом и вероятностью ошибок кратности d и более. Это предположение оправдано тем, что d для большинства кодов, используемых в режиме обнаружения ошибок, невелико по сравнению с k и n. Кроме того, вероятность появления таких ошибок определяется вероятностью появления d и более ошибок в кодовой комбинации, передаваемой по каналу связи.

Охарактеризуем поток ошибок, пропущенных в приемник сообщений средней вероятностью ошибки на бит, равной PПР и показателем группирования ошибок aпр.

Понятно, что PПР существенно меньше вероятности ошибки на бит в канале связи, а показатель группирования aпр имеет своей нижней границей показатель группирования ошибок в канале связи a, т. е. PПР < P и a aпр. Теперь можно записать равенство

k

1 aпр

e

n

1

a

PПР =

P:

d

2n k

d

Для упрощения расчетов примем aпр = a, тогда

PПР = 2ne k

k

P:

n

1

a

Для используемых в РОС-ППбл кодов справедливо nk ! 1 с ростом n

P

=

e

P

(будет показано далее). Поэтому принимаем ПР

. Следовательно, ве-

2n k

роятность ошибки в l-элементном знаке первичного кода, поступающего с выхода декодера в приемник сообщений, определяется как

Pош(l) = P( 1;l) = l1 a PПР = el1 a P:

2n k

Теперь можно сформулировать алгоритм выбора помехоустойчивого (n;k)-кода, оптимального в смысле критерия максимума скорости передачи.

90

1.Выбирается класс помехоустойчивых кодов. В настоящее время в двоичных системах передачи для систем РОС чаще всего используют циклические (n;k)-коды БЧХ.

2.Для кодов БЧХ естественной длины для различных значений n и k рассчитывается вероятность необнаружения ошибок в соответствии с заданными значениями p и a. Результаты расчетов сводятся в табл. 3.1 в колонку Pош. Данные о g(x) в табл. 3.1 заимствованы из [51] и будут использованы при выборе порождающего многочлена для найденного оптимального кода.

Таблица 3.1 Таблица результатов расчета вероятности необнаружения ошибок

											1 a			g(x)
n	k	k	n		k	d	P =	e	n			P	сомнож.	степени	корни
		n					ош	2n k	d				fi(x)	fi(x)	( j)
15	11	0,73		4		3							(23)8	4	1
	7	0,47		8		5							(37)8	4	3
	6	0,4		9		6							(03)8	1	0
31	26	0,84		5		3							(45)8	5	1
	21	0,86		10		5							(75)8	5	3
	16	0,52		15		7							(67)8	5	5
	11	0,35		20		9							(57)8	5	7
63	57	0,9		6		3							(103)8	6	1
	51	0,81		12		5							(127)8	6	3
	45	0,71		18		7							(147)8	6	5
	39	0,62		24		9							(111)8	6	7
127	120	0,94		7		3							(211)8	7	1
	113	0,89		14		5							(217)8	7	3
	106	0,83		21		7							(235)8	7	5
	99	0,78		28		9							(367)8	7	7
255	247	0,97		8		3							(435)8	8	1
	239	0,94		16		5							(567)8	8	3
	231	0,91		24		7							(763)8	8	5
	223	0,87		32		9							(551)8	8	7
511	502	0,98		9		3							(1021)8	9	1
	493	0,96		18		5							(1131)8	9	3
	484	0,95		27		7							(1461)8	9	5
	475	0,93		36		9							(1231)8	9	7
1023	1013	0,99		10		3							(2011)8	10	1
	1003	0,98		20		5							(2017)8	10	3
	993	0,97		30		7							(2415)8	10	5
	983	0,96		40		9							(3771)8	10	7

91

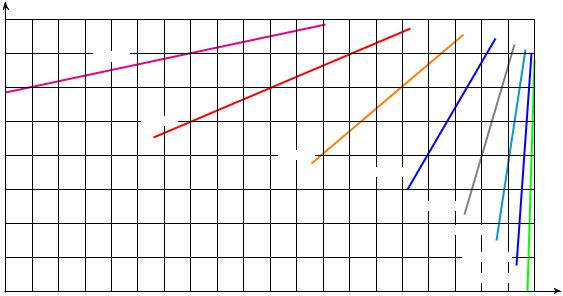
3. По данным табл. 3.1 по вычисленному значению Pош строятся графи-
ки семейства P					(C) = f			k	для различных n
на рис. 3.5.			ош				n							. Пример графика представлен
Pно
10 3
10 4				n = 15
10 5
10 6						n = 31
10 7												n = 63			n = 127
10 8																	n = 255
10 9																		n = 511
10 10																		n = 1023
10 11																			n = 2047		k=n
;33	;37	;40	;43		;47	;50	;53	;56	;60	;63	;66	;70	;73	;76	;80	;83	;86	;90	;93	;96	;99
0	0	0	0	0		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
			Рис. 3.5. Пример графиков семейства Pош(C) = f nk

4. На графике семейства Pош(C) = f nk для каждого значения n находится такое значение nk , которое удовлетворяет требованию по допустимой вероятности ошибки на выходе системы. Найденное значение nk заносится в табл. 3.2.

5. Для выбранных значений n и определенных в п. 4 значений nk в соответствии с заданными значениями p, a и рассчитанным h находятся значения r и R. Результаты сводятся в табл. 3.2.

Таблица 3.2

Таблица параметров для выбора кода

n	n	h	r = 1 [n(h + 1)]1 a p	Rc = n r	Rд = n 2 r
	k			k	k r
15
31
63
127
255
511
1023

92

	6. По данным табл. 3.2 строятся графики nk = f (n), r = f (n), Rд = f (n).
	Пример графиков представлен на рис. 3.6.
	0;99	k=n;r;r=(2 r);Rд
	0;90						k=n
	0;80	r=(2 r)					r
	0;70				Rд
	0;60
	0;50
	0;40
	0;30
	0;20
	0;10
	0;00								n
		24	25	26	27	28	29	210	211
			Рис. 3.6. Пример графиков nk = f (n), r = f (n), Rд = f (n)

7. По графику Rд = f (n) определяется максимальное значение относительной скорости Rmax и соответствующие ему значения nопт и nk . Умножением найденных значений nопт и nk находится значение k, соответствующее Rmax, а затем и (n k)опт.

Для найденных значений nопт, kопт, (n k)опт находятся ближайшие числа n, k и (n k), кратные длине комбинации заданного первичного кода, но так, чтобы избыточность (n k) не уменьшалась по отношению к (n k)опт. Эта задача легко выполнима, так как максимум функции Rд = f (n) достаточно «размытый». При этом допускается потеря скорости в пределах точности построения графика (1–2 %). На этом задача нахождения оптимального кода для РОС-ППбл считается выполненной. Эффективная скорость передачи определяется по формуле

Rэфф = Rmax Ne;

где Ne — заданная скорость передачи единичных элементов.

3.4.2. Проверка условия Pош(l) Pдоп(l)

Поиск оптимального кода основывался на выборе оптимальных параметров n и k кодов, удовлетворяющих заданным требованиям по достоверности. В ряде случаев может оказаться, что в пересчете достоверности с

93

n-элементного блока на l-элементный введенная избыточность (n k) будет значительно завышена. Поэтому, чтобы убедиться, что введенной избыточности достаточно для реализации требований по достоверности, предъявляемых к l-элементной комбинации первичного кода, дополнительно проводится

проверка,			основанная на проверке				выполнения	исходного неравенства
P	(l)		Pдоп(l).			Перепишем это	выражение	с учетом	значения
ош	(l)	e l1 a		p		P (l). Логарифмируя это		выражение,	получаем
P		:
ош			2n k			доп

(n k) (1 a)log2 l + log2 p + log2 e log2 Pдоп(l).

Если выбранное в п. 7 значение (n k) удовлетворяет этому соотношению, то считают выбор (n;k)-кода обоснованным.

В ряде случаев можно уменьшить избыточность, выбранную в п. 7. Действительно, если найдется значение (n k) меньше выбранного в п. 7, но кратное l и удовлетворяющее проверке, то следует именно его принять за оптимальное (n k) и, сохраняя nопт, кратное l, найти новое значение k. Эта процедура несколько повысит Rmax при выполнении требований по достоверности и, следовательно, она корректна в рамках используемого критерия.

3.4.3. Выбор порождающего многочлена g(x)

Выбор порождающего многочлена для найденного оптимального кода основывается на вычисленных значениях nопт и (n k)опт. Для выбора g(x) используется табл. 3.1. В этой таблице для представленных кодов БЧХ приведены порождающие многочлены g(x) в виде произведения неприводимых многочленов fi(x), степень каждого fi(x) и минимальная степень последовательности корней каждого из сомножителей ( a j). Индекс i неприводимого многочлена fi(x) возрастает с увеличением минимальной степени в последовательности корней. Например, f1(x) — неприводимый многочлен, последовательность корней которого содержит степень 1; f2(x) — соответствует многочлену с последовательностью корней, содержащей минимальную степень, не вошедшую в последовательность для f1(x) и т. д. Из приведенных в табл. 3.1 сомножителей порождающие многочлены циклических кодов можно получить следующим образом: g1(x) = f1(x), gi(x) = gi 1(x) fi(x).

При этом степень g(x) должна соответствовать параметру (n k) соответствующего кода. Такой метод составления порождающих многочленов позволяет построить циклические коды, у которых минимальное кодовое расстояние увеличивается по меньшей мере на 2 при увеличении числа сомножителей порождающего многочлена на 1.

В целях сокращения записи все многочлены указаны в восьмеричном представлении. Каждой восьмеричной цифре соответствует двоичная триада, как показано в табл. 3.3.

94

Таблица 3.3

Соответствие восьмеричных цифр и двоичных триад

Oct	0	1	2	3	4	5	6	7
Bin	000	001	010	011	100	101	110	111

Коэффициенты многочленов в двоичной записи располагаются в порядке убывания, т. е. коэффициенты при слагаемом высшего порядка расположены слева. Например, число (2415)8 обозначает многочлен в двоичной записи: 010100001101. Учитывая, что старшая степень находится слева, имеем

f (x) = x10 + x8 + x3 + x2 + 1:

Знание степени неприводимого многочлена и минимальной степени последовательности его корней позволяет найти всю последовательность корней для каждого многочлена g(x) в таблице. Для этого используется известное правило: «Если ai — корень f (x), то и a2i также его корень».

Надо помнить, что степени приводятся по mod n, где n — длина кодовой комбинации. Для приведенного многочлена ai = 5 и вся последовательность его корней имеет вид:

a5;a10;a20;a40;a80;a160;a320;a640;a257;a514:

Если найденный оптимальный код отсутствует в табл. 3.1 в явном виде, то следует его искать среди укороченных кодов (n i;k i). При этом надо ориентироваться на число (n k), а i определить из выражения i = nт nопт. Для этого выбираются табличные коды длины nт, для которых i > 0.

Например, по результатам расчетов найден оптимальный код с параметрами nопт = 80, kопт = 69 т. е. (n k)опт = 11. По исходным данным l = 5.

Для окончательного решения по параметрам кода необходимо, чтобы n и k были кратны 5, т. е. (n k) может быть либо 10, либо 15. Следует проверить по условию Pош(l) Pдоп(l) возможность использования (n k) = 10. Если это возможно, то решением будет код (80;70). Если же проверка покажет, что (n k) должен быть больше 10, то следует выбрать код (80;65).

В первом случае g(x) должен иметь степень 10, во втором — 15. В любом случае следует выбирать такой порождающий многочлен, который обеспечивает d > 3. Приемлемым решением является d = 4, но если при том же (n k) можно найти значение g(x), обеспечивающее большее d, то надо выбирать g(x) c большим d.

Для нашего примера с n = 80 следует рассматривать коды с длиной n от 127 и выше, ориентируясь на (n k). Для (n k) = 10 решение можно найти,

если выбрать f1(x) девятой степени, домножив его на (x + 1). В этом случае f (x) = (1021)8, т. е. f1(x) = x9 + x4 + 1, а g(x) = (x + 1)(x9 + x4 + 1).

95