
Лекция 1 Примеры задач линейного программирования
Как было отмечено во введении, задачи оптимизации, в которых целевая функция является линейной функцией своих аргументов, а условия, определяющие их допустимые значения, имеют вид линейных уравнений и неравенств, называются задачами линейного программирования. Линейное программирование начало развиваться в связи с задачами экономики, с поиском способов оптимального распределения и использования ресурсов и послужило основой широкого использования математических методов в экономике. В качестве примеров рассмотрим две типичных задачи линейного программирования: транспортную задачу и задачу о распределении ресурсов.
1. Транспортная задача
В городе имеются два склада муки и два хлебозавода. Ежедневно с первого склада вывозится 50 т муки, со второго – 70 т. Эта мука доставляется на хлебозаводы , причем первый завод получает 40 т, второй – 80 т. Перевозка одной тонны муки с первого склада на первый завод стоит 12 руб., на второй – 16 руб. Перевозка одной тонны муки со второго склада на первый завод стоит 8 руб., на второй – 10 руб. Требуется спланировать перевозки так, чтобы их суммарная стоимость была минимальной.
Чтобы решить
задачу, построим для нее математическую
модель. Обозначим через
![]() и
и![]() количество муки, которое нужно перевезти
с первого склада на первый и второй
заводы, а через
количество муки, которое нужно перевезти
с первого склада на первый и второй
заводы, а через![]() и
и![]() –
количество муки, которое нужно перевезти
со второго склада на первый и второй
заводы. Условия задачи приводят к системе
уравнений:
–
количество муки, которое нужно перевезти
со второго склада на первый и второй
заводы. Условия задачи приводят к системе
уравнений:
(1)
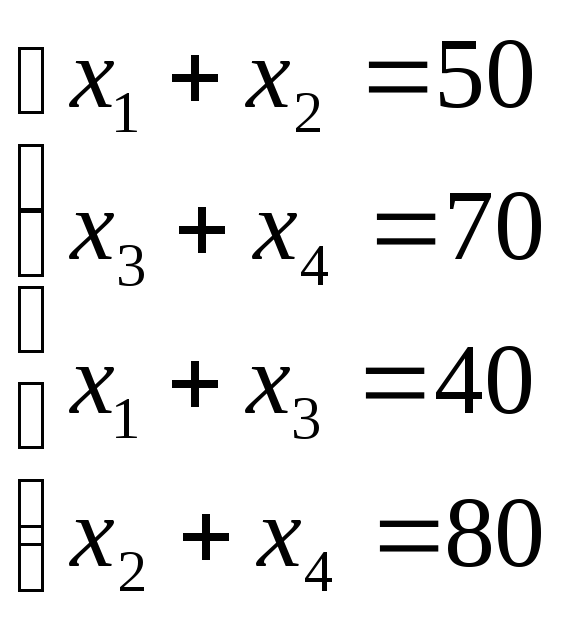
в которой
переменные
![]() – неотрицательные
числа:
– неотрицательные
числа:
(2)
![]() .
.
Общая стоимость всех перевозок определяется функцией:
(3)
![]()
![]()
Математическая
модель задачи такова: найти числа ![]() ,являющиеся решениями
системы (1) и удовлетворяющие условию
(2), при которых функция (3) имеет минимальное
значение.
,являющиеся решениями
системы (1) и удовлетворяющие условию
(2), при которых функция (3) имеет минимальное
значение.
Для решения задачи
можно применить «жадный» алгоритм,
используя самую дешевую перевозку
![]() в максимальном объеме:
в максимальном объеме:![]() =
40. Тогда значения остальных перевозок
определяются из системы (1) однозначно:
=
40. Тогда значения остальных перевозок
определяются из системы (1) однозначно:
![]() =
0,
=
0, ![]() =
50,
=
50, ![]() =
30.
=
30.
Суммарная стоимость
перевозок, вычисляемая по формуле (3),
будет составлять
![]() рублей.
Однако это решение не является оптимальным.
рублей.
Однако это решение не является оптимальным.
Рассмотрим внимательнее систему (1). Это система четырех уравнений с четырьмя переменными. Однако четвертое уравнение является следствием первых трех. Оно получается, если сложить первые два уравнения и из суммы вычесть третье. Таким образом, система (1) эквивалентна системе из первых трех уравнений:
(4)
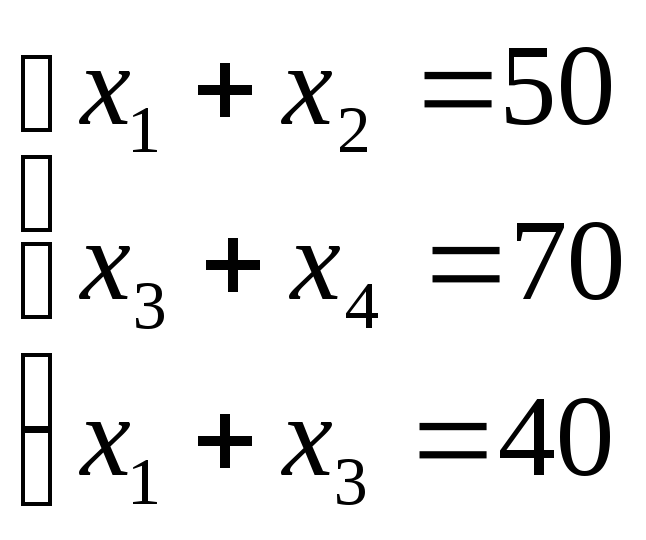
В системе (4) число
уравнений на единицу меньше числа
переменных, так что мы можем выбрать
одну из переменных, например ![]() ,
и выразить через нее с помощью уравнений
(4) три остальных. Получим формулы:
,
и выразить через нее с помощью уравнений
(4) три остальных. Получим формулы:
(5)
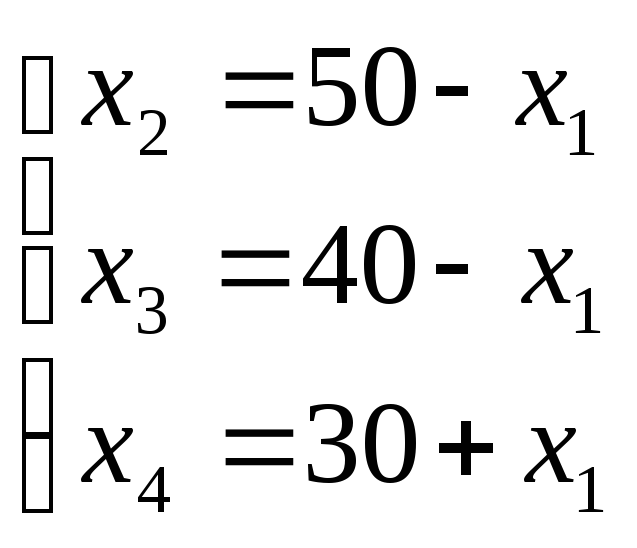
Учитывая условие (2), получаем систему неравенств:
(6)
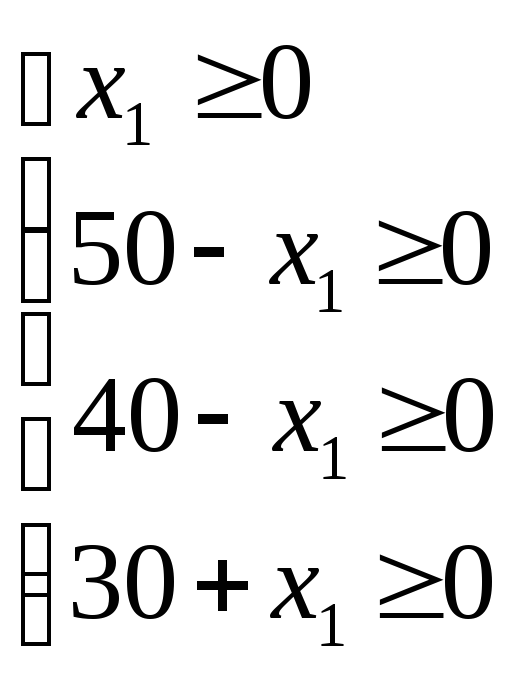
из которой следует, что выполняется неравенство:
(7)
![]()
Задавая любое
значение переменной
![]() ,
удовлетворяющее условию (7), и вычисляя
,
удовлетворяющее условию (7), и вычисляя![]() по формулам (5), мы получим один из
возможных планов перевозки.
по формулам (5), мы получим один из
возможных планов перевозки.
Вычислим суммарную стоимость соответствующего плана перевозки, для чего подставим формулы (5) в (3). В результате получим выражение:
(8)
![]()
![]()
Функция ![]() является функцией одной переменной
является функцией одной переменной
![]() и убывающей. Стоимость
и убывающей. Стоимость![]() окажется минимальной,
если переменной
окажется минимальной,
если переменной
![]() придать максимальное возможное
значение:
придать максимальное возможное
значение:![]() .
Значения
остальных переменных находятся по
формулам (5).
.
Значения
остальных переменных находятся по
формулам (5).
Таким образом, оптимальный план перевозок имеет вид:
![]()
![]()
![]()
![]()
Стоимость перевозок, вычисляемая по формуле (3), в этом случае составит 1340 рублей. При любом другом плане перевозок она окажется больше.
