ГОС математика / Мат. ан / 4,5,6
.doc|
Вопрос 4. Тригонометрические функции, их определения и основные свойства. В школьном курсе математики на первом этапе тригонометрические функции вводятся как функции острого угла в прямоугольном треугольнике. Опр. В прям-ом треугольнике синусом острого угла назыв. отношение противол-го катета к гипотенузе, косинусом – отношение прилежащего катета к гипотенузе, тангенсом – отношение противолежащего катета к прилежащему, котангенсом – отношение прилежащего к противолежащему. Sinα=a/c; cosα=b/c; tgα=a/b; ctgα=b/a
На втором этапе вводятся тригонометрические функции произвольного угла (произвольного числа), т.е. существенно расширяется область определения этих функций. Опр. Возьмем в прямоугольной системе координат Хоу Окружность радиуса 1 с центром в начале координат называют единичной окружностью. Пусть точка Р единичной окружности получена при повороте точки Р0 (1,0) на угол α. Синус угла α – это ордината точки Р, косинус – это абсцисса этой точки. tgα=sinα/coxα а≠π/2+πk, сtgα= coxα/sinα a≠πk.
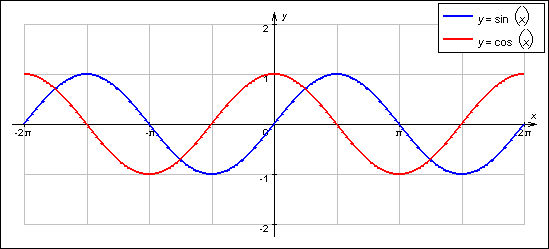
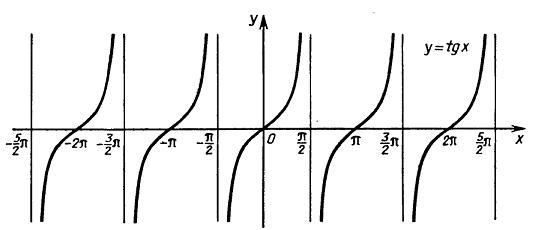
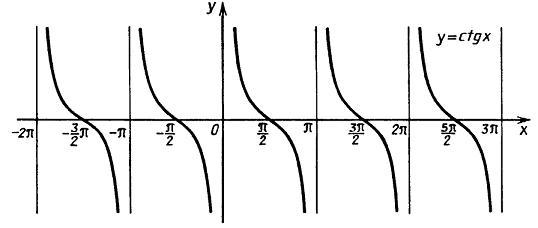
Опр: Если (.)Р числовой окружности соответствует числу t, то абсциссу (.)Р называют косинусом числа t и обозначают cost, а ординату (.)Р называют синусом числа t и обозначают sint. ( если каждому действительному Хэх ставится в соответствие единственное число у=sinx, то говорят, что задана функция синус х.) Опр: Отношение синуса угла t к косинусу того же угла называют тангенсам, а отношение косинуса угла t к синусу этого же угла называют котангенсом. Свойства тригонометрических функций: 1.Область определения. Опр. Это множество значений х из Х, которые обращают ф-ию в верное равенство. (y=sinх, y=cosx – D(f)=R;y=ctgx - D(f)=[-π/2+ πn; π/2+ πn].; y=tgx - D(f)=[ πn; π+ πn]). 2.Четность\нечетность. Опр. Множество Х называется симметричным относительно начала координат, если вместе с каждым х, оно содержит противоположное ему число (-х). Опр. ф-ия f, заданная на симметричном относительно нач.коорд. мн-ве Х называется четной (нечетной), если для любого х из Х f(-x)=f(x) (f(-x)=-f(x)). (y=sinх, y=tgx - нечетная, y=cosx –четная, y=ctgx – ни четная, ни нечетная). 3.Периодичность. Опр. ф-я f , заданная на некотором промежутке Х, наз периодич-ой с периодом к, где к≠0, если 1) Множество Х периодично (если с каждым х€Х, оно содержит (х±к)€Х) с периодом к. 2)для любого х€Х f(х±к)=f(x). 1. y=sinх, y=cosx – периодичны, период 2πn. 2. y=tgx,y=ctgx - периодичны, период πn, кроме кроме х=π/2+πn для тангенса и х=π+πn для котангенса. 4. Непрерывность. (y=sinх, y=cosx – непрерывны; y=tgx – Непрерывна на интервале (-π/2+πn;π/2+πn).; y=сtgx – Непрерывна на интервале (πn;π+πn)) 5.Ограниченность. Опр. Ф-ия наз-ся ограниченной на множестве А из X, если множество значений, принимаемых этой ф-ией на А ограниченно некот.числом В. Ограниченное множество имеет точную верх. И нижн.границу. Опр. Ф-ия неограниченна, если для люб.числа В найдется х, что |f(x)|>B. (y=sinх, y=cosx - Ограниченны [-1;1], y=tgx, y=сtgx – Неограниченны.) 6.Монотонность. Опр. Ф-ия наз-ся монотонной, если она возрастает либо убывает на промеж-ке А из Х. Опр. Ф-ия называется возраст.(убывающ) на подмножестве А, если для любого х1, х2 из А, таких что х1<x2, следует что f(x1)=<f(x2) (f(x1)=<f(x2)). Все тригонометр-е функции на R не являются монотонными, поэтому необратимы на R. В таком случае выделяют участок монотонности, чаще всего [-π/2,π/2]. На нем, например, ф-я sinх монотонна на [-π/2,π/2] и принимает все свои значения от -1 до 1. Свойства косинуса аналогичны свойствам синуса. (y=sinх - Возрастает на [-π/2+2πn; π/2+2πn]; Убывает на [π/2+2πn; 3π/2+2πn]; y=cosx - Убывает на [0+2πn; π+2πn].Возрастает на [π+2πn; 2π+2πn]; y=tgx - Возрастает на (-π/2+πn; π/2+πn); y=сtgx - Убывает на (0+πn; π+πn).) 7. Наибольшее/ наименьшее значение ф-ции. (y=sinх – Уmax=1 в (.) х=-π/2+2πn, У min=-1 в (.) х=π/2+2πn ; y=cosx - У max=1 в (.) х= 2πn, У min=-1 в (.) х= π+2πn; y=tgx, y=сtgx – Нет ни наиб., ни наим. значения.) 8. Область значений. Опр. это множество значений, которые может принимать х из Х: (y=sinх, y=cosx - E(f)=[-1;1]; y=tgx ,y=сtgx - E(f)=R.) 9. Дифференцируемость. Все тригонометр функции непрерывно и неограниченно дифференцируемы во всех точках которых определены.
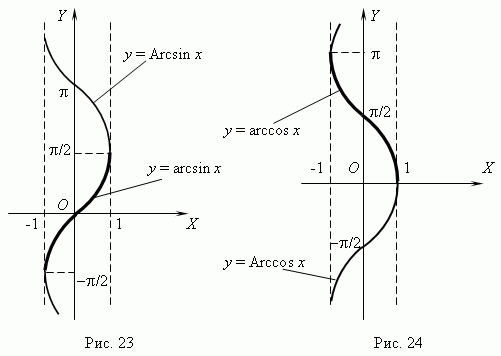
Обратные тригоном функции. Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: -1 < x <+1 ; их области значений: -π/2 < y<π /2 для y = arcsin x и 0 < y<π для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные ( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и x = 1 у функции y = arccos x).
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: -∞< x <+∞ ; их области значений: -π/2 < y < π/2 для y = arctan x и 0 < y < π для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные ( y = arctan x – возрастающая функция; y = arccot x – убывающая );
- только функция y = arctan x имеет единственный ноль ( x = 0 ); функция y = arccot x нулей не имеет.
В ШКМ у Мордковича эта тема изучается в 10 классе очень подробно и достаточно на высоком уровне. Определения даются с помощью числовой окружности. Подробно рассмотрены свойства синуса, косинуса и тангенса. |
Вопрос 5. Дифференцируемость функции. ! ф-я y=f(x)опред-на в т. х0 и её окрестности. Опр: Функция f(x) наз. дифференцируемой в т. х0, если ее приращение в этой точке можно представить виде ∆f(х0)=A* ∆х+α(∆х)* ∆х, где А – некоторое число независящее от ∆х; α(∆х) – б.м.величина по сравнению с ∆х, т.е. lim α(∆х)=0 при ∆х->0. Если ф-я диф-ма, то она непрерывна.
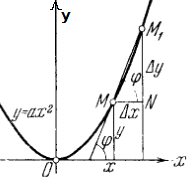
Пример: y=x2, ∆y=f(x0+∆x)-f(x0)=(x0+∆x)2-x02=x02+2x0∆x+(∆x)2-x02=2x0∆x+∆x∆x, 2x0 – число, ∆x –бмф => y=x2 – диффер-ма в т х0. Опр: Если ф-я имеет произ-ю в т. х0, то она диффер-ма в этой точке. Опр: Дифференциалом функции в некоторой точке наз.произведение производной в этой точке на приращение независимой переменной: dy=f’(х0)* ∆х. T (необх.и достат.усл-ие диф-ти): Если ф-ия f(x) диф-ма ф т. х0, то она непрер-на в т. х0. Док-во: ! ф-ия f(x) диф-ма в т. х0 , то приращение функции можно представить виде ∆f(х0)=A* ∆х+α(∆х)* ∆х. Перейдем к пределу при ∆х0 lim∆f(х0)=lim(A* ∆х+α(∆х)* ∆х) lim∆f(х0)=0(т.к в скобках беск-но мал.величины) при ∆х0. => по опр.нерерывности функции в точке на языке приращения, f(x) – непр-на в т. х0 Замечание: данная Th не явл-ся обратной (напр: y=|x|) Опр: Производной функцией f(x) в т. х0 наз. Предел отношения приращения функции к приращению аргумента, когда последнее 0
Заметим, что из опр. => что производная в точке это всегда некоторое число. Т: для того чтобы функция f(x) была диф-ма в т. х0 чтобы существовала производная этой ф-и в точке. Док-во: (=>) f(x) – диф-ма в т. х0. Нужно д-ть что в этой точке существует производная. По опр.приращение можно представить в виде ∆f(х0)=A* ∆х+α(∆х)* ∆х, где А – некоторое число независящее от ∆х, α(∆х) – б.м.величина ∆f(х0)=A* ∆х+α(∆х)* ∆х |∆х≠0
Перейдем в посл.неравенстве к пределу при ∆х0.
По опр. f ’(x)=A (<=) Производная в т. х0 существует, необходимо доказать, что ф-я диф-ма в этой точке. Из опр.производной известно, что
По необх. и достат. условию существования предела =>
Умножим обе части неравенства на ∆х и получим: ∆f ‘(х0)= f(х0)* ∆х + α(∆х)* ∆х, f ‘(х0)=А – число, независящее от ∆х, а значит по опр. => f(x) диф-ма в точке х0 #
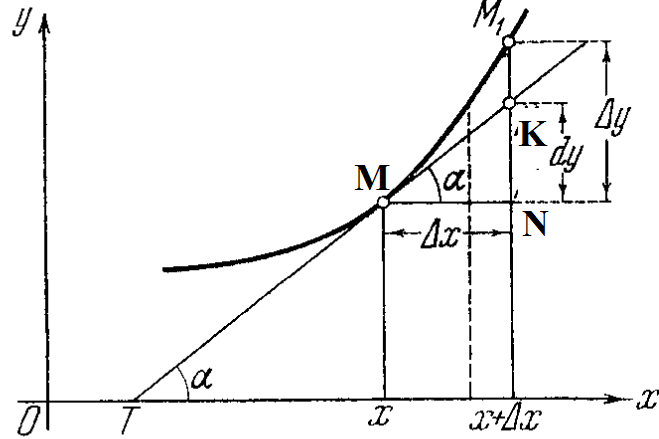
Геом. смысл: Производная фун-ии f(x) в т. x0 есть угловой коэф-ет касат-ой к графику фун-и в т. x0, это tg угла наклона между касат-ой, проведен-ой в т. x0 и полож-ым направлением ОХ.
Пример
Найти угловой коэффициент касательной
к графику f(x)=2sinx в т
Геом.
Смысл диф: Значение
дифференциала в т x0
равно
линейному приращению касательной в
точке x0
.
Механ. смысл: Если некоторая материальная т. М совершает прямолинейное неравномерное движение по закону s=S(t), то значение производной в т t0 –это мгновенная скорость в момент времен t0 . Правила дифференцирования:
1.
2.
Если ф-и и(х)
и v(x)
диф-мы в т.
х0,
то в т. х0
диф-ма ф-ия y=u+v,причем:
Док-во:
[y=y(u,v);Δу
= y(u
+ Δu)
+ (v
+ Δv)
- y(u
+ v)].
Придадим х0
приращ. ∆х
=lim
+ lim
3. Если ф-и и(х) и v(x) диф-мы в т. х0, то в т. х0 диф-ма ф-ия y=u+v,причем: (u • v)' = и' v + u v' Док-во: Придадим х0 приращ. ∆х ≠0.Это приращ.вызовет у ф-ий u(x) и v(x) приращ Δu,Δv. =>ф-ия получит приращ Δу.
=lim
=u•
v'+v•
u'+
lim
Т.к u,v-диф-мы
в т. х0,то
она непрер-на => Δu0,Δv0
при ∆х0.
lim Т.о (u • v)' = и' v + u v'
4.
Если ф-и и(х)
и v(x)
диф-мы в т.
х0,
то в т. х0
диф-ма ф-ия y=u(x)+v(x),причем:
5.
Если ф-и и(х)
и v(x)
диф-мы в т.
х0
и v(x)
≠0, то в т. х0
диф-ма ф-ия
Док-во:
!y=
=lim
=lim
=lim
=
= 6.произ-ая сложной ф-ии
Если функция
u=g(x) имеет произ-ю
Док-во: Дадим х приращ ∆x≠0. Тогда u и у получат приращ. Δu и Δу.
Т.к. ф-я u = g(x)
дифф-ма=>, непр-на, то Δu
7.произв-ая обратной ф-ии
!ф-ия х = f(y) монотонна
и дифф-ма на (a, b) и имеет в точке у этого
интервала произв. f'(y)≠ 0. Тогда в х
обратная ф-я у = Инвариатность формы 1 порядка. Мы имеем след.ф-лу для вычисления диф-ла: df(x)=f‘(x)dx. Оказывается, что эта формула сохраняется и в том случае, когда не явл. независимой переменной, а явл. некоторой ф-ей от другой переменной. Докажем это. Пусть у=f(x) диф-ма в т. х0, а х=φ(z) – диф-ма в т. z0. Рассмотрим сложную у= f (φ(z)) и д-м, что df (х0)=f ‘(х0)*dx у= f (φ(z)) будет ф-ей от переменной z . dy= yz’dz= yx’* xz’dz = yzdx= f ’(х0)dx. Итак, мы получили, что df (х0)=f ‘(х0)*dx и в случаях, когда х явл.некоторой ф-ей от другой переменной. В этом и состоит инвариатность формы диф-ла 1 порядка.
Иначе говоря, диффер-л ф-ции имеет один и т от же вид произведения производной по некоторой переменной, независимо оттого, является ли эта переменная в свою очередь ф-цией или независ переменной. |
Вопрос 6. Условия постоянства, монотонности и выпуклости функции. Th(условия постоянства и монотонности) !ф-ия y=f(x) опред-на на [a;b]непр-на на нем и дифф-ма на (a;b).Тогда: 1)Ф-ия у=f(x) явл. пост-ой на [a,b] f’(x)=0 для любого хÎ(a,b). 2)
Ф-ия у=f(x) возр.(убыв.) на [a,b] f’(x)≥0
(f’(x)≤0)
3)
если f’(x)>0
(f’(x)<0)
При док-ве используется.Th Лагранжа: !
ф-ия y=f(x) опред-на на [a;b],причем: 1) f(x)
непр-на на [a;b] 2) f(x) дифер-ма на(a;b), тогда
внутри [a;b] найдется точка с:
Док-во: 1)1.(необх-ть) очевидно, т.к. c’=0, c=const. (f(x) постоянная) 2.(дост-ть)
пусть f’(x)=0
f(x)=const на [a,b]. ■ 2) 1.(необх-ть) пусть ф-ия f возр. на [a,b]. Возьмем любые т. х и х0 такие, что a<x0<x<b. Заметим, что f(x) ≥f(x0). Рассм. отношение:
lim
2.
(дост-ть) пусть f’(x)
≥0
f возр на [a,b]. ■ 3) (док-во анагогично док-ву дост-ти) Замечание:
выпол-ся
только для достат-ти,необх-ть от сюда
не след-ет.(напр: y= Пример. y=x3 на [-1;1] – диф-ма, y'>0 во всех т [-1;1] кроме 0. y’(0)=0, т.е касат горизонтальна, y- возрастающая. Опр. кривая у=f(x) выукла вверх (вниз) на Х, если она располож. ниже (выше) любой касат-ой, провед. к каждой точке промежутка Х. (касательная выше функции). Ан-но опр.вниз Th
(неох и дост усл вып-ти) Пусть
ф-ия у=f(x) опред. и непрер на [а;b] и диф-ма
в (а;b). Для того чтобы ф-ия у=f(x) была
вып. вниз на [а;b]
чтобы на этом отрезке ее график лежал
не ниже касат., провед. к графику в Th (дост. усл. вып-ти). Пусть
ф-ия у=f(x) опред-на и непрер. на [а;b],
дважды диф-ма в (а;b). Тогда, если
f’”(x)>0
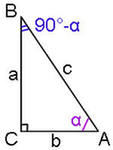
Геом.смысл т.
Лагранжа:
BC=f(b)-f(a),AC-b-a
=> Пример.
y=sinх на [0; ШКМ: Т.Лагранжа присутствует в шкм, но доказывается не строго. На ее основе обосновывается условия монотон возраст или убыв ф-ии на нек-ом промежутке. Т(дост. усл. вып-ти). Пусть ф-ия у=f(x) опред-на и непрер. на [а;b], дважды диф-ма в (а;b).
|

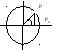


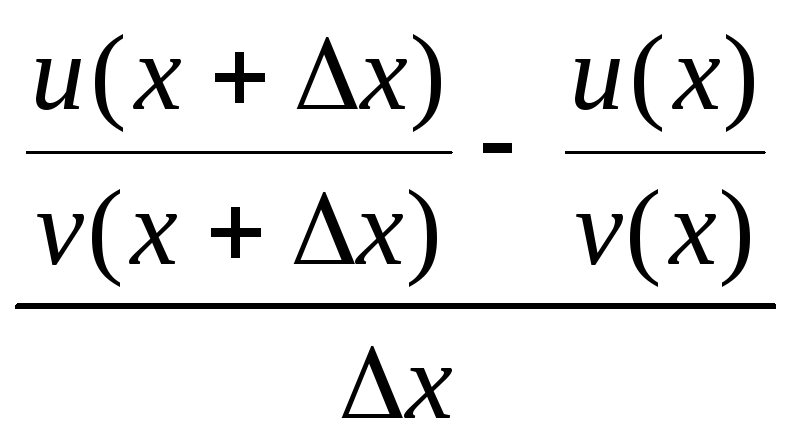 =
=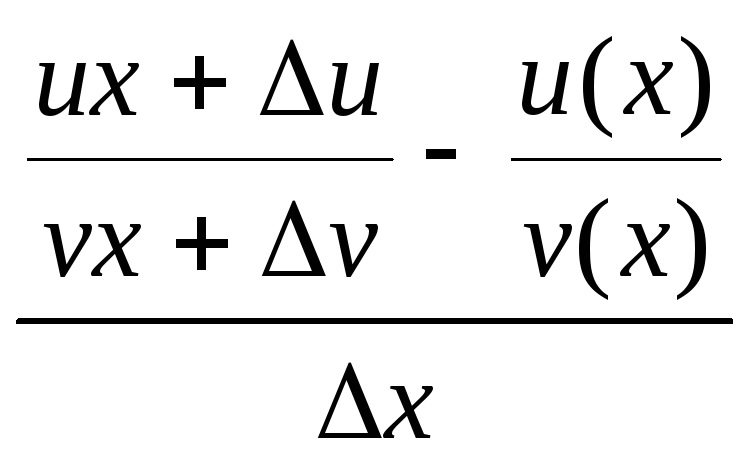 =
=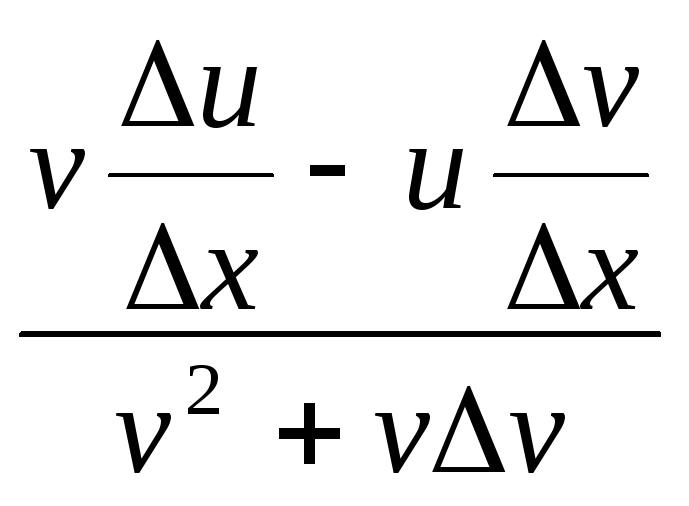 =
=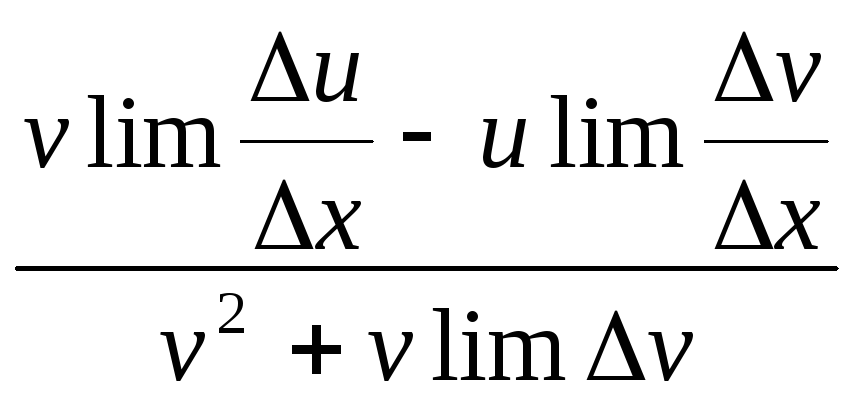 =[u,v-диф-мы,то
они непр-ны=>∆u,
∆v,
0]
=[u,v-диф-мы,то
они непр-ны=>∆u,
∆v,
0]