
ГОС математика / Мат. ан / 1,2,3
.doc|
Вопрос 1. Функции (отображения). Предел функции в точке и на бесконечности. Опр. При заданных множ. X и Y под отображением f множ. X к множ. Y понимаем соответствие, при кот. каждому эл-ту множ. x X сопост-ся нек-ый вполне определенный эл-т у Y (при этом у зависит от х). Опр. Пусть Х числовое множество. Говорят, что на Х задана функция f, если хХ поставлено в соответствие одно и только одно число y = f(x). x - независимая переменная (аргумент), y - зависимая перемен.(функция). Х – Область определения. Y – обл.значения. Св-ва: - четность (ф-я наз.четной (нечетной) если выполняется 2 условия: Обл.опред.ф-и сим-на относит-но ); f(-x)=f(x)-чет., f(-x)=-f(x) – нечет.) Функция является ни четной ни нечетной (функция общего вида), когда не выполняется симметричность. ПР. cos x, x3, x3 для [-1,1] - периодичность X – T-периодичное, если
f:
X→Y-
T-периодичная,
если D(f)
– T-периодична
и
Пример: y=x2 – периодическая. D(f)=R
!T=1
Мн-во R- период-е, причем его периодом является любое число.
Y=sinx – периодическая. - монотонность Функция возрастает, если
Функция не возрастает, если
Функция убывающая, если
\ Функция неубывающая, если
Пример: y=x3+3x, доказать, что строго возрастает?
- обратимость (если каждому значению у из У ставится в соответствие только одно значение х)
Пример: Опр. Число А наз-ся пределом числовой послед-ти, если для любого ε > 0 сущ. n0 принад. N, что для любого n принад. N: n > n0 вып-ся нер-во |х
n-а|<ε.
( Геом. смысл. A-Ɛ < xn < A+ Ɛ . Все точки начиная с n=N+1,N+2,..N+m,…. лежат внутри (А- Ɛ , А+ Ɛ ). Вне интервала лежат х1,х2,..,хn. Чем < Ɛ тем > N. Опр.Коши. Число А наз. пределом ф-ии f (x) в точке а если для любого сколь угодно малого числа ε > 0 найдется такое число δ ( ε ,а)> О, что для всех х, удовл-ших нер-ву 0<|х – а| < δ , вып-ся неравенство |f (х) – A| < ε. Г.С. |f (х) — А |< ε , А - ε < f(х) < А + ε. Какую бы полосу ограниченную прямыми у = А – ε, y = А + ε мы не взяли, найдется такая проколотая окрестность δ-0 в точке а, что все точки графика с абсциссами из этой окрестности находятся внутри выбранной полосы. Опр, Число А наз. пределом ф-ии f (х) при х→∞, если для любого ε> 0 найдется такое δ ( ε ,а)> О , что для любого х: |х| > δ, |f (х) – A| < ε Геом.смысл Нер-во |f (х) — А |< ε равносильно нер-ву А - ε < f(х) < А + ε. Учитывая последнее, можно дать след. геом-ое истолкование предела ф-ии на бесконечности - Таким образом, какую бы полосу ограниченными прямыми у=А-ε и у=А+ε, мы не взяли, найдется такое число δ>0, что какое бы число х из (-∞;- δ)и( δ;+∞) мы не взяли. Все точки графика f(x) будут находиться внутри этой полосы.
Св-ва предела: Т1 Если функция имеет предел в данной точке, то она ограничена в некоторой окрестности данной точки Док-во: Lim f(x)=A <=> для любого ε >0 сущ. ∂>0: для любого х∊Д(х): 0<|x-x0|<∂ => |f(x)-A|< ε. Рассмотрим любое х из окрестности (х0-∂, х0+∂) => А- ε <f(x)<A+ ε. Пусть ε =1= ε 0. Lim f(x)=A при х --> x0 => для любого ε 0 >0 сущ. ∂0>0: для любого х∊Д(х): 0<|x-x0|<∂0 => |f(x)-A|< ε. А- ε 0<f(x)<A+ ε 0. Левая часть и правая это числа => функция ограничена сверху и снизу. # T2. Пусть у=f(x) и у=g(x) определ. на некотором множ. Х, за исключ. может быть некоторой точки х0 этого множ. Тогда если сущ. lim f(x)=А и lim g(x)=В при х --> x0, то
Док-во:
Док-во:
При х --> x0
Т3
Ели (теорема о предельном переходе в неравенстве) Док-во(от противного) пусть a>b.
Т4 Теорема о пределе промежуточной функции
Док-во:
Подход в школе: На базовом уровне понятии числовой послед-ти не рассмат. => нет понятия предела. Понятие функции опред. на интуитивном уровне:если значение переменной х как угодно близка к значению х0 и при этом значение f(x) так же приближается к некоторому числу А, то говорят, что А является пределом f в х0. На проф.уровне рассматр. понятие числовой функции как N-го аргумента. Определения пределов даются только по Гейне. Место: на понятии предела основаны основные понятия школьных начал анализа (производная и интеграл). |
Вопрос 2. Непрерывность функции в точке и на множестве. Пусть функция f определена в точке х0 и в некоторой ее окрестности. Onp.(основное) Если предел ф-ии в точке х0 и значение ф-ии в этой точке равны, т.е. lim f(x)= f(x0) при х→ x0. то ф-я f-наз. непрерывной ф-ей в точке xо. Опр. (Коши) Ф-я f наз. непрерывной в точке x0 если для любого ε >0 найдется такое δ>0, что для всех х, удовлетворяющих нер-ву |х-х0|<δ, выполняется неравенство |f(x)-f(x0)|<ε. Пояснения: если ф-я непрерывна в точке, то какую бы окрестность ε этой точки мы не взяли, на оси х всегда найдется такая δ окрестность точки, что при отображении ф-и образы этих точек попадут из δ окр-ти в ε окр-ть. Опр. (на языке прирощ.) Ф-я f(х) наз. непрерывной в т x0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. (Если lim ∆y=0 при ∆х --> 0, то ф-я f (х) наз. непрерывной в т x0. Причем ∆х ≠0, х0+∆х∊Х, ∆y=f(х0+∆х)-f(x0)-прирощение функции.) Опр.(предел слева, справа) Ф-я f(х) наз. Непрерывной слева(справа), если предел слева равен значению функции в т. х0
Пояснения: Функция будет непрерывной в точке х0 , если предел слева и справа в этой точке равен значению функции f(x0). Обратное утверждение также верно, если предел слева равен пределу права – они равны значению ф-и в этой точке, то ф-я будет непрерывна в т. х0 Простейшие св-ва непр. ф-ий:
Док-во:
Т.к.f
непрерывна в х0,
Док-во:
f(x)
– непр.в т.
g(x)
– непр.в т.
по осн.опред.мы получаем, что f+g – непр.в т. х0
Частное f(x)= Док-во:
1) (произв.) f(x)
– непр.в т.
g(x)
– непр.в т.
по осн.опред.мы получаем, что f*g – непр.в т. х0
2) (частное) f(x)
– непр.в т.
g(x)
– непр.в т.
Опр. Функция наз-ся непр-ой на множ.Х если она непр-на в каждой точке этого множ. Опр. Функция непрерывна на [a;b], если она непрерывна в каждой точке интервала (a;b) и
T. (Вейерштрасса)1: (об ограниченности функции) Если ф-я f определена и непрерывна на отрезке [а,b], то на этом отрезке она ограничена.
Т.е.
Док-во: (от противного) Предположим, что f(x) непр.на отрезке [а,b], но не ограничена на нем. Разобъем отрезок [а,b] пополам, тогда на которой из половин f(x) будет неогр.(иначе, если бы ф.была огр.на обоих половинах отрезка, то это несоответствовало бы нашему предположению) Возьмем ту половину [а,b], где ф.неогр.и обозначим ее [а1,b1]. Теперь разобьем отрезок [а1,b1] пополам, и выберем ту половину отрезка [а1,b1], где она будет неогр. и обозначим ее [а2,b2]. Продолжим описанный процесс до ∞. В результате получим систему вложенных отрезков
При n∞, поэтому построенная система отрезков является стягивающейся. А по принципу стяг. системы отрезков, существует и един.общая точка для всех отрезков.
Обозначим ее с.
Точка
(с- δ;с+ δ) в которой f(x) будет огр..
Возьмем
n
настолько большим, что отрезок
Сл-но получили противоречие.
Примечание: с
одной стороны, посл-ть отрезока
с другой – на всем интервале (с- δ;с+ δ) f(x) должна бытьогр. Полученное противоречие снимает допущение, таким образом #
Т. (Вейерштрасса)2: Если ф-я f определена и непр-на на отрезке [а,b], то на этом отрезке она достигает своего наибольшее и наименьшее значение. Док-во: По 1-й т-ме Вейерштрасса ф-я f ограничена на отрезке [а,b], след-но, мн-во ее значений имеет точные границы. Пусть sup{E(f)}=M, inf{E(f)}=m. Док-м, что сущ-ют такие точки x1 и x2, что f(x1) =М, f(x2)=m. Допустим, что нет такой точки x1 в кот. F(x1)=M. Тогда f(x1)<M для всех х из [а,b].
Расс-м вспомогательную
ф-ю g(х)=
M-
Т. (Больцано-Коши)1: Если ф-я f определена и непрерывна на отрезке [а.b] и на концах этого отрезка она имеет значения разных знаков, т.е. f(a)*f(b)<0, то на отр.[а,b] найдется по крайней мере одна точка а<с<b, в которой ф-я равна 0, т.е. f(c)=0 Док-во:
Пусть
f(a)<0,f(b)>0.Разделим
[a,b]пополам
точкой
Если не =, то хотя
бы на одном из [a,
Мы имеем lim an=c, limbn=c при n ∞. Воспользуемся непр-тью функции на [a,b]=> f(x) непр-на в точке х=с. По опред. непр-ти в точке по Гейне lim f(an)=f(c)<=0, lim f(bn)=f(c)>=0 =>f(c)=0. # Т. (Больцано-Коши)2: Если ф-я f определена и непрерывна на отрезке [а,b] и на концах этого отрезка принимает различные значения, те f(a)≠f(b), то эта функция принимает все значения из [f(a); f(b)]. Док-во: Надо доказать, что для любого µ из [f(a); f(b)] найдется такая точка с из [a;b], что f(c)=µ.
Введем вспомогательную
ф-ю φ(х)=f(x)-µ
и рассмотрим эту ф. Ф. непрерывна как
разность двух непр.ф-й, и φ(а)<0, а
φ(b)>0,
т.к. φ(а)=f(a)-µ,
а φ(b)=
f(b)-µ
и f(a)<µ<f(b)
=> применим 1ю т.Б-К ф. φ(х) получим,
Непрерывность в школе. введения понятия предела ф-ии в точке, нахожд. наиб.инаим. значений. |
Вопрос 3. Показательная и логарифмическая функции, их определения и основные свойства.
Опр:
!Х-мн-во
всех дейст-ых чиел. Отобр-ие,кот-е
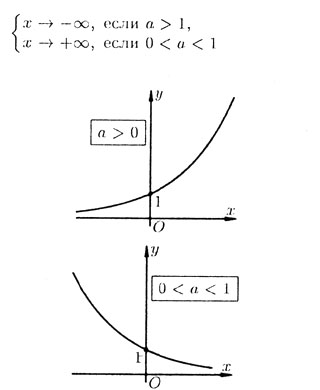
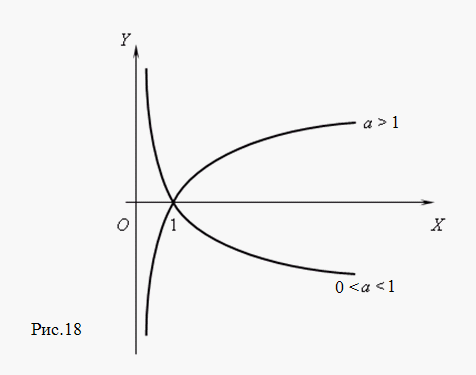
Пр-р. y=2x; y=ex; y=(1/2)x Свойства показательной ф-ции: 1.Область определения D(f)=(-∞;+∞) 2.а0=1 3.При а>1 функция строго возрастает, при 0<a<1 – строго убывает. 4.При а>1 lim ax=+∞, lim ax=0, при 0<a<1 – наоборот. x→+∞ x→-∞ 5.Показ функция непрерывна. 6.Не является ни четной, ни нечетной. 7.Не ограничена сверху, ограничена снизу. 8.Не имеет ни наибольшего, ни наименьшего значений. 9.E(f)=(0;+∞) 10.Выпукла вниз. Исходя из свойств функций, построим графики показательной функции.
Опр. Логарифмической функцией наз функция, обратная к показательной функции y=ax. Поэтому ее график получается из графика показ функции с помощью преобразования симметрии относительно прямой у=х.
Пр-р. y=log2x; y=log1/2x По теореме об обратной функции и определению обратной функции получаем свойства логарифмической функции. 1.D(f)=(0;+∞) 2.E(f)= (-∞;+∞) 3.loga1=0 4.При а>1 logax строго возрастает на (0;+∞), При 0<а<1 logax строго убывает на (0;+∞) 5.Логариф функция непрерывна. 6.Не является ни четной, ни нечетной. 7.Не ограничена сверху, не ограничена снизу. 8.Не имеет ни наибольшего, ни наименьшего значений 9.Выпукла вверх при а>1, выпукла вниз при 0<а<1
Свойства логарифмов: 1.Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел: loga(x*y)= logax+ logay (x,y>0) 2.Логарифм частного равен разности логарифмов делимого и делителя или логарифм дроби равен разности логарифмов числителя и знаменателя: loga(x/y) = logax- logay (x,y>0) 3.Логарифм степени равен произведению показателя степени на логарифм основания степени: logaxα=αlogax (х>0) ШКМ:основана на понятии степени числа от натур-го до рац-го показателя, с иррац-ым показа-нм опирается с ссылкой на высш.матем. Ф-ия однозначная.Место:св-ва ф-ий имспол-ся при решений ур-ий и нерав-в. |




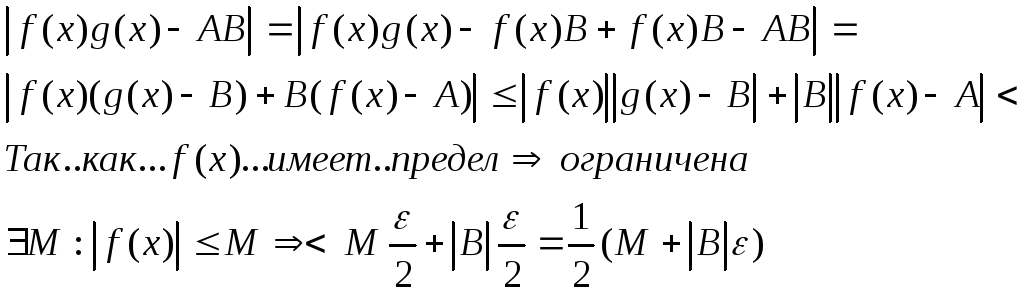
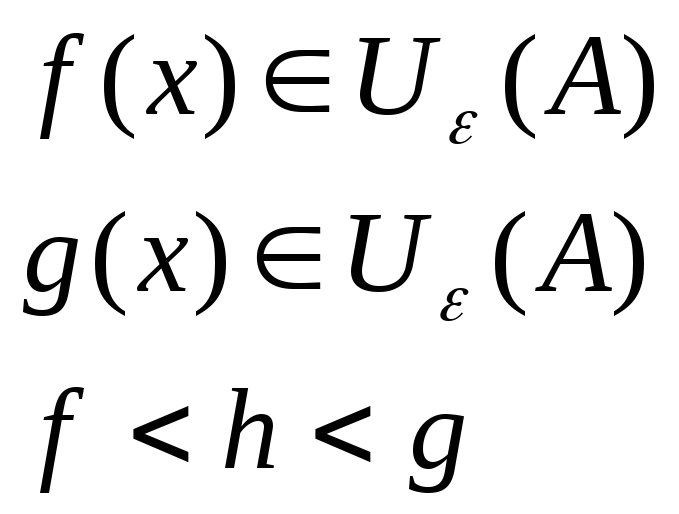
 Графики
функций y=f(x)
и y=f(-x)
симметричны относительно оси у. Кривую
показательной функции наз экспонентой.
Графики
функций y=f(x)
и y=f(-x)
симметричны относительно оси у. Кривую
показательной функции наз экспонентой.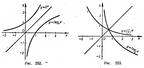
 график
наз логарифмическая кривая
график
наз логарифмическая кривая