13. Размещения и сочетания

Df. 4.20: Набор элементов Х_i1, Х_i2, …,Х_ip из множества X={ х₁,х₂, … , х_m } называется выборкой объема r из n-элементов или (n,r)-выборкой.

Df. 4.21: Выборка называется упорядоченной, если порядок следования элементов в ней задан. Иначе, выборка называется неупорядоченной.

Зам: Две упорядоченные (не упорядоченные) выборки с одними и теми же элементами, но различным порядком их следования, считаются различными (одинаковыми).

Зам: В выборке могут допускаться или не допускаться повторения элементов.

Df. 4.22: Упорядоченная (n,r) выборка, в которой повторение элементов допускается (не допускается) называется (n,r) размещением с повторениями (без повторений).

Df. 4.23 Неупорядоченная (n,r) выборка, в которой повторение элементов допускается (не допускается) называется (n,r) сочетанием с повторением (без повторений).

Df. 4.24: Перестановкой множества Х, состоящего из n элементов называется (n,r) размещение без повторений.

Введем следующие обозначения:

– число всевозможных (n,r) размещений с повторением

– число всевозможных (n,r) размещений без повторением

– число всевозможных (n,r) сочетаний с повторениями.

всевозможных (n,r) сочетаний без повторений.

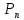- число всевозможных перестановок.

Лемма 4.5:

Д-во: Каждое (n,r) размещение представляет собой упорядоченную последовательность длины r. Поскольку повторение элементов в этой последовательности допускается, то 1-ый член последовательности можно выбрать n-способами, 2-ой n-способами тоже и т.д. Тогда по обобщенному правилу произведения получаем: Чтд

Замечание: Введем следующее обозначение: n!= n, при этом 0!=1

Лемма 4.6:

Д-во: Каждое (n,r) размещение представляет собой упорядоченную последовательность длины r. Т.к. повторение элементов в этой последовательности не допускается, то 1-й член последовательности можно выбрать n-способами, 2-ой – (n-1)-способами, 3-ий – (n-2)-способами и т.д. Тогда по обобщенномуправилу произведения получаем, что:

Следствие:

Лемма 4.7 :

Лемма 4.8

14. Бином Ньютона

Используя лемму 4.7: можно доказать след. утверждения:

Лемма 4.10:

Д-во: По лемме 4.7 получаем: , Чтд.

Лемма 4.11 :

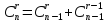
Д-во: Имеем Чтд.

Лемма 4.12:

Лемма 4.13(Бином Ньютона):

Зам: Из леммы 4.13 получаем след. следствия:

Следств 1:

Д-во: Из леммы 4.13 при х=1, у=1 получаем (1+1)ⁿ=2ⁿ=

Следств 2:

Д-во: При x=-1,y=1

Следств 3:

Следств 4:

Зам: Числа называются биномиальными коэффициентами.

Зам: Биномиальные коэффициенты образуют так называемый треугольник Паскаля.

Вычислив соотв. значения мы получим след. треугольник

Зам: Проанализировав треугольник Паскаля можно заменить несколько закономерностей:

1. По боковым сторонам треугольника расположены единицы. Это следует из свойств =1; =1

2. Треугольник симметричен относительно вершины. Это следует из леммы 4.10: =

3. Каждый элемент треугольника равен сумме двух расположенных над ним элементов. Это следует из леммы 4.11: =