
- •Формулы логики высказываний и логики предикатов
- •Равносильность в логике высказываний и влогике предикатов
- •Тавтологии
- •Понятие предиката. Кванторы
- •Нормальные формулы логики предикатов
- •Языки. Аксиомы. Правила вывода
- •Вывод. Вывод из гипотез
- •Теорема Дедукции. Следствия
- •Примеры выводимых формул
- •Непротиворечивость ив
- •Полнота ив
- •Правило суммы, произведения
- •Размещения и сочетания
- •Бином Ньютона
- •Разбиение. Полиномиальная теорема
- •Булевы функции
- •Формулы. Равносильность формул
- •Метод рекуррентных соотношений
- •Решение линейных рекуррентных соотношений
- •Понятие производящей функции
- •Интуитивное понятие алгоритма
- •Машины Тьюринга. Вычислимые функции
- •Рекурсивные функции
- •Алгоритмически неразрешимые проблемы
- •Нумерации машин Тьюринга
- •Критерии эффективности алгоритма
- •Полиномиальные и неполиномиальные алгоритмы
- •Основные понятия теории графов
- •Маршруты, цепи, циклы
- •Виды графов
- •Способы задания графов
- •Эйлеровы графы
- •Геометрическая реализация графов
- •Деревья. Лес.
- •Остовное дерево
- •Важнейшие числовые характеристики графов
- •Основные понятия теории кодирования
- •Критерий однозначности алфавитного кодирования
- •Алгоритм распознавания однозначности кодирования
- •Коды Хэмминга
- •Понятие множества
- •Операции над множествами. Свойства
- •Формулы включения и исключения.
-
Формулы. Равносильность формул
1/Ф-лы
Df.1.: Пусть F – некоторое мн-во булевых ф-ций, тогда:
-
Каждая переменная явл ф-лой над F.
-
Символы 1 и 0 явл ф-ми над F.
-
Каждое выражение
 явл формулой
над F.
явл формулой
над F. -
Если
 ф-ла над F,
и A1,
A2
,…, An
– ф-лы
над F,
то выражение f(A1,
A2
,…, An)
– явл ф-ой над F.
ф-ла над F,
и A1,
A2
,…, An
– ф-лы
над F,
то выражение f(A1,
A2
,…, An)
– явл ф-ой над F.
2/ Равносильность
Df.2.:
Пусть
 – совокупность всех переменных входящих
хотябы в одну из ф-л А, В, тогда ф-лы А и
В - наз равносильными, если они принимают
одинаковые значения на любом наборе
значений переменных
– совокупность всех переменных входящих
хотябы в одну из ф-л А, В, тогда ф-лы А и
В - наз равносильными, если они принимают
одинаковые значения на любом наборе
значений переменных
 . В этом случае пишут: А
. В этом случае пишут: А .
.
Замече.: Все равнос-ти, кот-е имели место в логике выск-ий остаются в силе и для рассматриваемых формул. Кроме того, имеются новые равносильности, связанные с вновь введенными ф-циями:
|
23.
A |
Где
|
28.
|
|
|
24.
A |
30.
A
|
||
|
25.
A/B
|
31.
A |
||
|
27.
A |
32.
A |
||
Замеч.: Пользуясь имеющими равносильностями ф-лы можно преобразовывать к более простому специальному виду.
Замеч.: Тождественно-исинные, тожд-ложные и выполнимые ф-лы определяются точно так же как и в логике высказываний.
-
Метод рекуррентных соотношений
Сущность этого метода заключается в том, что решение этой же задачи с меньшими значениями переменных. При этом связь между исходной задачей и задачей с меньшими значениями переменных задаётся с помощью, так называемых, рекуррентных соотношений.
Df.1.: Рекуррентным называется соотношение, в котором для вычисления некоторого члена числовой последовательности используются значения предыдущих членов этой же последовательности.
Зам: Мы уже знакомы с одним рекуррентным соотношением. Это соотношение задаётся
Леммой.1. : =
= .
.
Пример: В 1240г. Итальянский математик Фибоначчи предложил, так называемую, задачу о кроликах. Её суть состоит в следующем: на ферме имеется 1 пара кроликов. Сколько пар кроликов будет через n месяцев при условии, что
1)через месяц пара становится плодоносящей;
2)в один месяц от каждой пары появляется приплод в размере одной пары;
3)кролики никогда не умирают.
Обозначим искомое число через fn. Каждый месяц на ферме будут молодые и старые кролики. Число молодых пар кроликов через n месяцев обозначим через Mn, число старых пар кроликов – через Cn. Тогда fn=Mn+Cn; fn+1=Mn+1+Cn+1. Кроме того, в каждом месяце число молодых пар кроликов будет=числу старых пар кроликов в предыдущем месяце, т.е. Мn+1=Cn. Кроме того, все молодые пары кроликов через месяц станут старыми, поэтому Cn+1=Mn+Cn=fn. Аналогично Cn+2=Mn+1+Cn+1=fn+1; Cn+3=Mn+2+Cn+2=fn+2. Тогда fn+2 =Mn+2+Cn+2= Mn+2+ fn+1= Cn+1+fn+1=fn+fn+1. Т.о. fn+2=fn+fn+1. Поскольку f0=0, f1=1, то мы получаем следующую последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21. 34, 55, 89, …
-
Решение линейных рекуррентных соотношений
Пусть
дано рекуррентное соотношение
fn+2=fn+fn+1,
где f0=0,
f1=1.
Тогда для вычисления n-ого
члена необходимо вычислить все предыдущие
члены. Конечно же хотелось бы fn,
зная только n.
Для некоторых рекуррентных соотношений
это можно сделать. Рассмотрим рекуррентное
соотношение с постоянными коэффициентами.
Методику решения таких рекуррентных
соотношений рассмотрим на следующем
примере. Пример:
Пусть n+2=fn+fn+1,
где f0=0,
f1=1.
Будем считать, что fn=pn.
Тогда рассматриваемое рекуррентное
соотношение перепишется в виде
pn+2=pn+pn+1.
Разделим обе части этого соотношения
на pn:
р2=1-р1
=> р2-р-1=0
Решив это уравнение, получим корни :
р1= ;
р2=
;
р2= .
Тогда рекуррентное соотношение будет
иметь вид fn=c1(
.
Тогда рекуррентное соотношение будет
иметь вид fn=c1( )n+c2
(
)n+c2
( )n.
Если n=0,
то f0=0=c1+c2;
n=1
=> f1=1=c1(
)n.
Если n=0,
то f0=0=c1+c2;
n=1
=> f1=1=c1( )+c2
(
)+c2
( ).
Мы получили систему уравнений: с1+с2=0
и c1
).
Мы получили систему уравнений: с1+с2=0
и c1 +c2
+c2 =1.
с1=
=1.
с1= ,
с2=
-
,
с2=
-
 .
Тогда рекуррентное соотношение примет
вид fn=
.
Тогда рекуррентное соотношение примет
вид fn= .
Последняя формула известна под названием
Бине для нахождения чисел Фибоначчи.
Замечание: Исходя из рассмотренного
примера можно изложить общую методику
решения рекуррентных линейных соотношений
с постоянными коэффициентами. В общем
случае линейное рекуррентное соотношение
с постоянными коэффициентами имеет
вид: xn+k=ak-1xn+k-1+ak-2xn+k-2+…+a0xn
(1). Где ai-постоянные
коэффициенты, x1,…,xk-
начальные значения. Решение соотношения
находим в виде xn=pn.
Подставим это в соотношение (1). В
результате получим полином k-ой
степени: pk=ak-1pk-1+…+a1p+a0.
Это ур-ние имеет k-корней
p1,
… , pk.
Тогда общее решение соотношения будет
иметь вид: xn=
.
Последняя формула известна под названием
Бине для нахождения чисел Фибоначчи.
Замечание: Исходя из рассмотренного
примера можно изложить общую методику
решения рекуррентных линейных соотношений
с постоянными коэффициентами. В общем
случае линейное рекуррентное соотношение
с постоянными коэффициентами имеет
вид: xn+k=ak-1xn+k-1+ak-2xn+k-2+…+a0xn
(1). Где ai-постоянные
коэффициенты, x1,…,xk-
начальные значения. Решение соотношения
находим в виде xn=pn.
Подставим это в соотношение (1). В
результате получим полином k-ой
степени: pk=ak-1pk-1+…+a1p+a0.
Это ур-ние имеет k-корней
p1,
… , pk.
Тогда общее решение соотношения будет
иметь вид: xn= ,
здесь ci-постоянные
коэф-ты и их будем находить исходя из
начальных условий x1,
… , xk.
В результате получим систему линейных
уравнений относительно постоянных
коэф-тов.
,
здесь ci-постоянные
коэф-ты и их будем находить исходя из
начальных условий x1,
… , xk.
В результате получим систему линейных
уравнений относительно постоянных
коэф-тов.

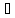 B
B B
B A
A -
-


 (B
(B (A
(A B)
B)
 (B
(B (A
(A B)
B)
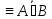 ;
26. A
;
26. A ;
;


 B
B
 ;
;

