Дискр. мат._1 ПФ

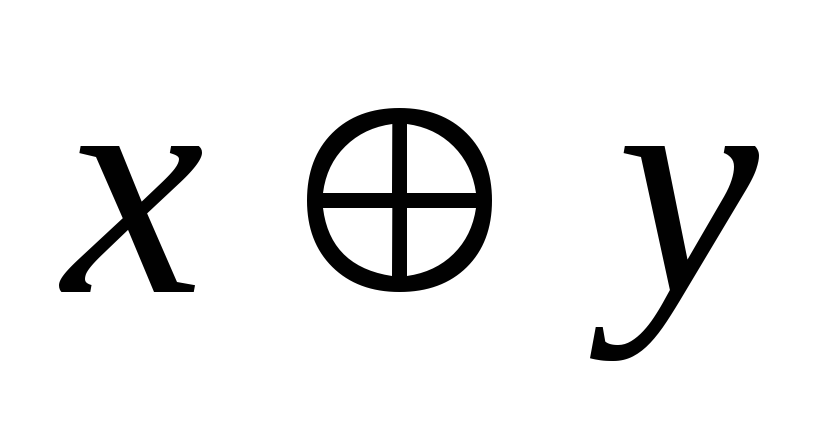x	y
0	0	0
0	1	1
1	0	1
1	1	0

Алгебра, построенная на основе этих операций, называется алгеброй Жегалкина и обладает следующими свойствами:

1. коммутативность;

2.  ассоциативность;

3. дистрибутивность умножения относительно сложения;

4. свойства констант;

5. закон идемпотентности для умножения;

6. закон приведения подобных членов при сложении.

Операции отрицания и дизъюнкции в алгебре Жегалкина записываются формулами:

(1)

, т.е.

(2).

Если в формуле алгебры Жегалкина раскрыть все скобки и произвести упрощения по свойствам 1 — 6, то получится формула, имеющая вид суммы конъюнкций. Такая формула называется полиномом Жегалкина.

Теорема. Для каждой логической функции существует полином Жегалкина, и притом единственный.

Особо важную роль играют функции, полиномы Жегалкина которых имеют вид: где – константы 0 или 1. Такие функции называются линейными. Все функции от одной переменной – линейные. Среди функций от двух переменных линейных только две: — сложение по модулю 2, и ~ () — эквиваленция.

Чтобы построить полином Жегалкина для произвольной булевой функции достаточно записать ее ДНФ или КНФ и воспользоваться формулами (1) и (2). Но иногда это проще сделать с помощью метода неопределенных коэффициентов.

П ример: Построить полином Жегалкина для функции .

Решение: Полином Жегалкина для функции трех переменных имеет вид:

.

Итак,

Из рассмотренного выше следует, что все булевы функции можно получить, используя лишь некоторые из них, например, конъюнкцию, дизъюнкцию и отрицание или даже только конъюнкцию и отрицание (дизъюнкцию и отрицание), а можно константу 1, конъюнкцию и сложение по модулю 2, а можно все функции записать с помощью одной операции | (штрих Шеффера) или (стрелка Пирса).

Возможность представления любых булевых функций с помощью ограниченного их числа имеет важное практическое значение при их аппаратной реализации.

Определение. Множество булевых функций называют функционально полной системой, если любая логическая функция может быть представлена в виде суперпозиции функций из (формулой над ).

Важную роль в решение задачи о полноте системы имеют замкнутые классы функций, то есть множества функций, суперпозиции которых не выводят за пределы данных множеств. Например, конъюнкция конъюнкций снова конъюнкция, линейная функция от линейных функций снова линейная функция. Особую роль играют замкнутые классы :

— множество линейных функций,

— множество монотонных функций,

— множество самодвойственных функций,

— множество функций, сохраняющих 0, т.е. таких, что ,

— множество функций, сохраняющих 1, т.е. таких, что .

Понятие монотонной булевой функции несколько отличается от одноименного понятия в анализе. На множестве двоичных векторов или наборов значений переменных , вводится отношение частичного порядка: , если существует такое, что , а для остальных индексов

Определение. Функция называется монотонной, если для любых двоичных -мерных векторов и из того, что , следует, что 

Если для некоторой функции , а , для какого-нибудь , то эта функция уже не монотонна. По таблице булевых функций двух переменных видно, что монотонны 0, 1, , , , , в то время как , , , , |, не являются монотонными.

Для проверки монотонности можно пользоваться следующим критерием:

Теорема. Булева функция, отличная от 0 и 1, монотонна тогда и только тогда, когда существует представляющая ее булева функция без отрицаний (т.е. функция выражается через конъюнкцию и дизъюнкцию своих переменных).

Если получить такую формулу не удается, то, возможно, что функция не монотонна, т.е. найдутся такие наборы и , что , а . Эти наборы следует явно указать.

Пример. Функция монотонна по критерию, а про функцию сразу ничего сказать нельзя, так как наличие в формуле отрицания еще не означает, что нет другой булевой формулы без отрицания. Однако , а , следовательно, функция не монотонна.

Определение. Функция называется самодвойственной, если для всех .

Из определения следует, что функция не является самодвойственной, если найдется такой набор , что . При векторном задании функции самодвойственность или несамодвойственность очевидны: функция самодвойственна, если вектор антисимметричен относительно своей середины , и несамодвойственна в противном случае.

Пример. самодвойственна, а несамодвойственна, так как

Американским математиком Э. Постом (1897-1954) доказана следующая

Теорема. Для полноты системы функций 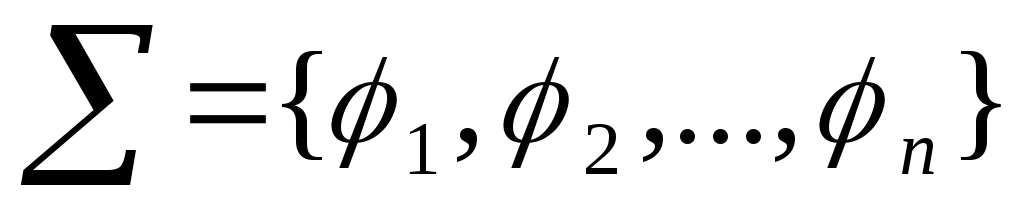необходимо и достаточно, чтобы для каждого из классов в нашлась функция , не принадлежащая этому классу.

Пример. Проверить. является ли функционально полной система .

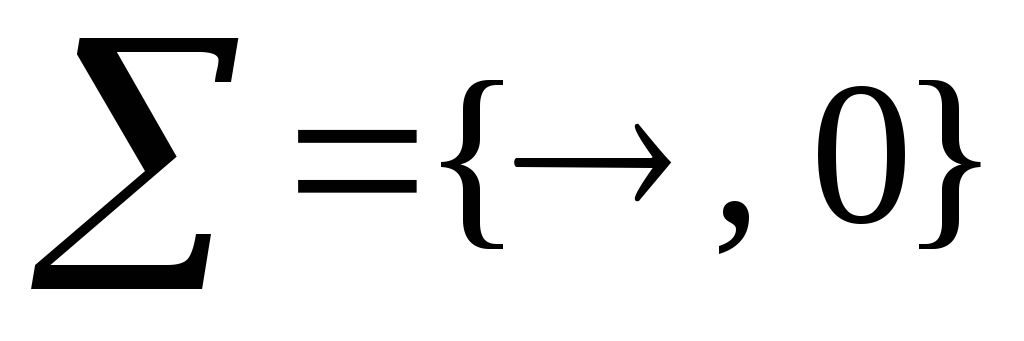Решение. Составим таблицу, в которой будем отмечать “непринадлежность” функции классам, указанным в теореме Поста.

	-	-	-	-	+
0	+	+	-	+	-

1. Функция .

Найдем для нее полином Жегалкина. Это можно сделать методом неопределенных коэффициентов, а можно непосредственно переписывая отрицание и дизъюнкцию через операции алгебры Жегалкина:

Функция не является линейной (есть ).

, а — это противоречит определению монотонности, следовательно, не является монотонной.

, т.е. не сохраняет 0.

, т.е. сохраняет 1.

, т.е. , значит, не является самодвойственной.

2. Функция .

линейная (нет конъюнкции).

монотонна, т.к. для всех .

, сохраняет 0.

, не сохраняет 1.

, не является самодвойственной.

По таблице видим, что для каждого из классов нашлась функция, ему не принадлежащая, значит  – функционально полная система.

Если из системы убрать , то останется 0, который один не дает функционально полной системы (он принадлежит ); если же убрать 0, то останется , которая сохраняет 1. Поэтому система  образует базис.

Замечание:

1. Ранее отмечалось, что из функций двух переменных только  и линейные, поэтому нелинейность можно было определить сразу.

2. После того, как таблица заполнена для первой функции, для второй достаточно было проверить лишь принадлежность или непринадлежность ее классу .

Рассмотренные вопросы можно изучить по указанной литературе, точнее: [3, гл. 1, § 1.1—1.6, гл. 5, §5.1—5.5], [4, гл. 3, § 1—12], [6, гл. 3, § 3.1—3.3], [7, разд. 2, гл. 4, § 4,3—4.5], [8, гл. 1, § 1.1—1.2], [9, гл. 3], [11, гл. 6, § 6.1—6.9], [12, ч. 1, гл. 1].

15