4.2. Уравнения с разделяющимися переменными

Дифференциальное уравнение вида

,

где и- непрерывные функции, называется уравнением с разделяющимися переменными.

Запишем производную в эквивалентной форме как отношение дифференциалов, тогда

.

Для отыскания решения этого уравнения необходимо разделить в нём переменные. Умножим обе части уравнения на и поделим на, полагая, что, имеем

.

Теперь левая часть уравнения содержит только переменную , а правая – только. Интегрируя обе части этого уравнения, получим

.

Таким образом, найден общий интеграл уравнения .

Пример 26. Найти частное решение дифференциального уравненияпри начальных условиях.

Решение

Перепишем данное уравнение в виде

.

Функция является решением уравнения. Остальные решения найдём, разделив переменные в уравнении и проинтегрировав его:

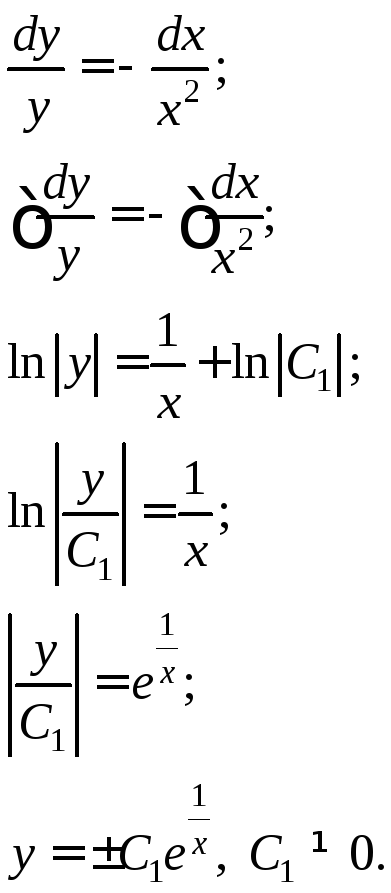
Так как ранее найденное решение можно получить из последнего соотношения, положив, то

- общее решение.

Из условия находим

.

Частное решение имеет вид

.

4.3. Линейные уравнения первого порядка

Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид

,

где и- непрерывные функции переменной.

В случае, когда тождественно равна нулю, уравнение называется однородным, в противном случае – неоднородным.

Рассмотрим один из способов решения уравнения : будем искать решение в виде .

Одна из неизвестных функций илиможет быть выбрана произвольно, а другая – должна определяться из уравнения .

Найдём . Подставляяи её производную в уравнение , получим

или

.

Найдём какое-либо частное решение уравнения

.

Тогда из уравнения функция является решением уравнения

.

Задача решения линейного дифференциального уравнения свелась к решению двух уравнений с разделяющимися переменными и .

Пример 27. Найти общее решение дифференциального уравнения

.

Решение

Будем искать решение в виде , тогда

и при подстановке функции и её производной в уравнение имеем

,

или

.

Положим или, откуда

Найдём какое-либо частное решение этого уравнения, например, при .

.

При равенство обратится в уравнение

или

.

Окончательно имеем

.

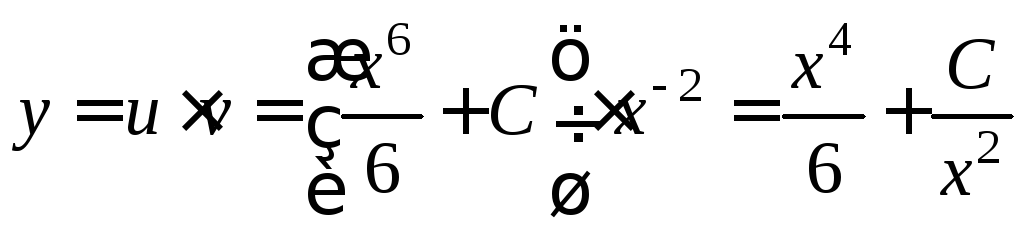Пример 28. Найти выражение объёма реализованной продукциии его значение при, если известно, что кривая спроса имеет вид, норма акселерации, норма инвестиций,, а функцияудовлетворяет уравнению [3, гл. 12].

Решение

Подставим значения коэффициентов и функции в дифференциальное уравнение, получаем

.

После упрощения оно принимает вид

или

.

Выполняем разделение переменных

.

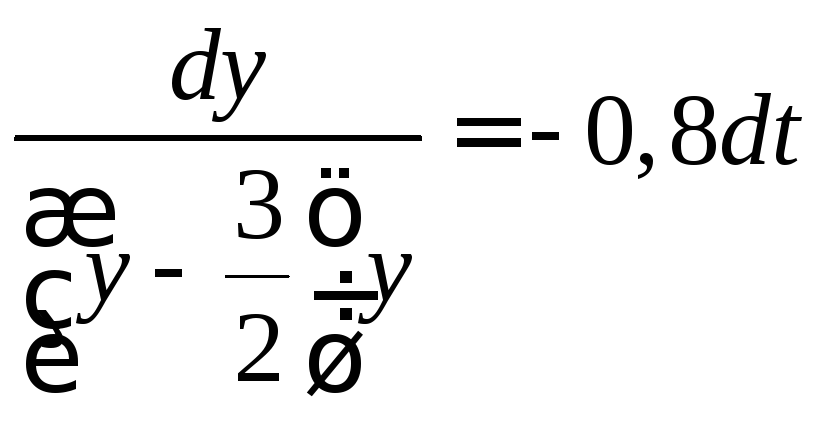Интегрируем почленно это уравнение с разделёнными перемен­ными, получаем

где .

Учитывая, что , получаем.

Подставляем найденное значение и выражаем, имеем

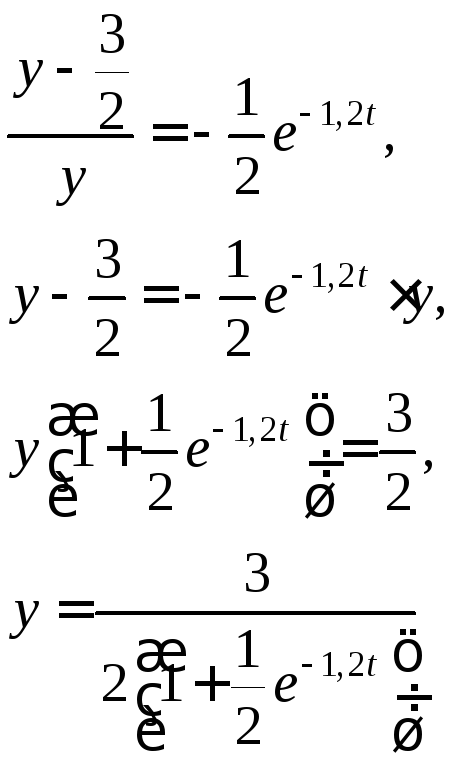
или

.

Найденное значение .

5. Вопросы к экзамену

1. Неопределённый интеграл и его свойства.

2. Неопределённый интеграл от основных элементарных функций.

3. Замена переменной в неопределённом интеграле.

4. Формула интегрирования по частям.

5. Определённый интеграл и его свойства.

6. Вычисление определённого интеграла. Формула Ньютона-Лейбница.

7. Замена переменной в определённом интеграле.

8. Интегрирование по частям в определённом интеграле.

9. Вычисление площадей с помощью определённого интеграла.

10. Вычисление объёмов тел вращения с помощью определённого интеграла.

11. Функции нескольких переменных, способы задания и свойства.

12. Частные производные функций нескольких переменных, их смысл в различных задачах.

13. Экстремум функции двух переменных. Необходимое и достаточное условия существования экстремумов.

14. Условный экстремум. Функция Лагранжа.

15. Метод наименьших квадратов.

16. Производная по направлению. Вектор градиент.

17. Полный дифференциал и полное приращение функций неско­льких переменных.

18. Обыкновенные дифференциальные уравнения. Условия существования и виды решений уравнений первого порядка.

19. Уравнения с разделяющимися переменными.

20. Линейные дифференциальные уравнения первого порядка.