26.Определение нормали к поверхности. Определение нормали к поверхности

Нормаль к поверхности представляет её локальную кривизну, а, следовательно, и направление зеркального отражения. Если известно аналитическое описание поверхности, то нормаль вычисляется непосредственно. Для многих поверхностей бывает задана лишь их полигональная аппроксимация. Зная уравнение плоскости каждой грани можно определить направление внешней нормали. В алгоритмах компьютерной графики для удаления невидимых линий и поверхностей используются только рёбра и вершины, поэтому, чтобы объединить их с моделью освещения, необходимо знать значение нормали не только на рёбрах, но и в узловых точках.

Определение нормали в вершине рассматриваемой модели рис.9.2.1 можно представить как

,

где 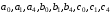- коэффициенты уравнений плоскостей трех многоугольников, окружающих.

Если же уравнения плоскостей не заданы, то нормаль к вершине можно определить, усредняя векторные произведения всех рёбер, пересекающихся в вершине

.

Если вектор не нормируется, то его величина и направление зависит от количества и площади конкретных многоугольников, а также от количества и длины конкретных рёбер. Сильнее проявляется влияние многоугольников с большей площадью и более длинных рёбер.

21.Интерполяция точечного каркаса функции полиномами. Интерполяция полиномами

Рисунок 5.1.1.б отображает квадратичный полином вида (1), при этом, коэффициенты определяются исходя из условия

, (1)

где - узловые точки, определяющие параболу участка кривой.

По аналогичным принципам задаётся кубический сплайн (рис. 5.1.1.с), отображённый на этом же рисунке с большими значениями кривизны.

Основной недостаток интерполяционных полиномов, приближающих функции, заключается в том, что поведение функции в окрестности какой-либо точки определяет поведение её в целом.

За счёт этого знак кривизны в узловой точке для соседних сегментов, как правило, меняется на противоположный (рис.5.1.1), а значит, узловая точка стремится к перегибу и исходная сетка не соответствует приближению зрительного восприятия функции через её каркас.

Аппаратом приближения, свободным от этого недостатка, являются сплайны.

Предположим, что кубическая парабола, заданная в параметрической форме:

. (3)

проходит через две точки (рис.5.1.2), обозначенные соответственно и, в которых известны значения производныхи. Это означает, что заданы четыре необходимых и достаточных условия для определения четырех коэффициентов в выражении (3).

Если определены четыре условия, то вычисление коэффициентов в выражении (3) выполняется довольно просто:

,

,

,

и

.

Отсюда можно вывести

,

,

,

.

Определив кубическую параболу (рис. 5.1.2) между точками и , для нахождения следующей дуги кривой между точками инеобходимо в точкахи приравнять значения самой кривой и ее первых производных и задать значение вектора .

На рисунке 5.1.2 вектора для -ой и-ой точек определяются как

, .

Таким образом, шаг за шагом определяется последовательность дуг кубической кривой, соединяющей точки и имеющей непрерывные касательные в этих точках.