индив. задания 6

10. ; ; .

Вариант 26

1. .

2. .

3. .

4. .

5. .

6. ; .

7. ; .

8. .

9. .

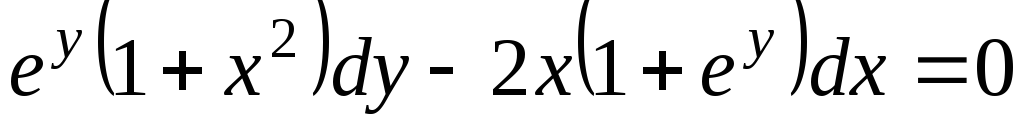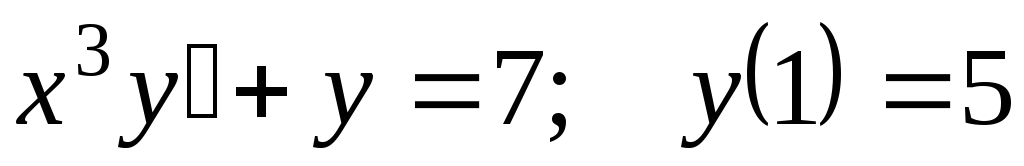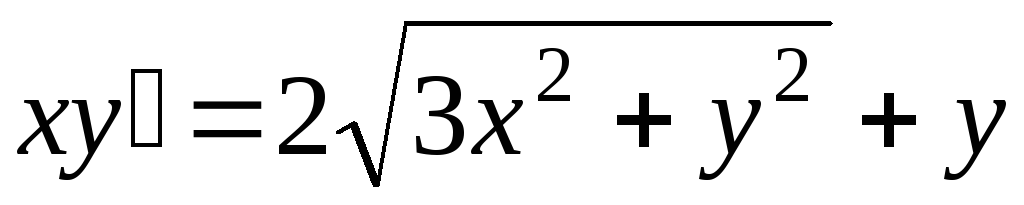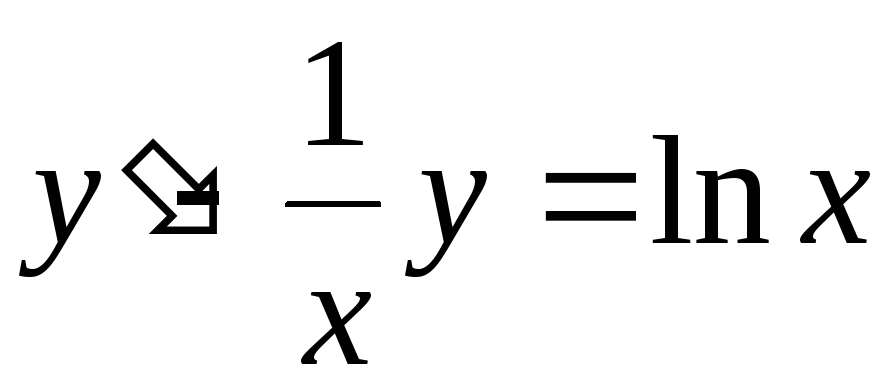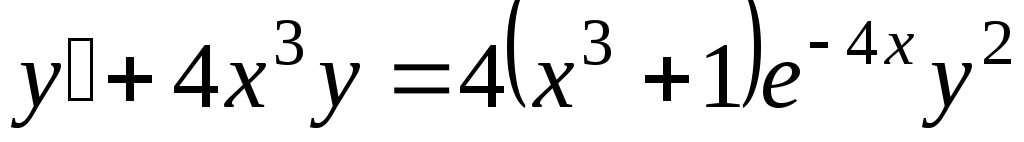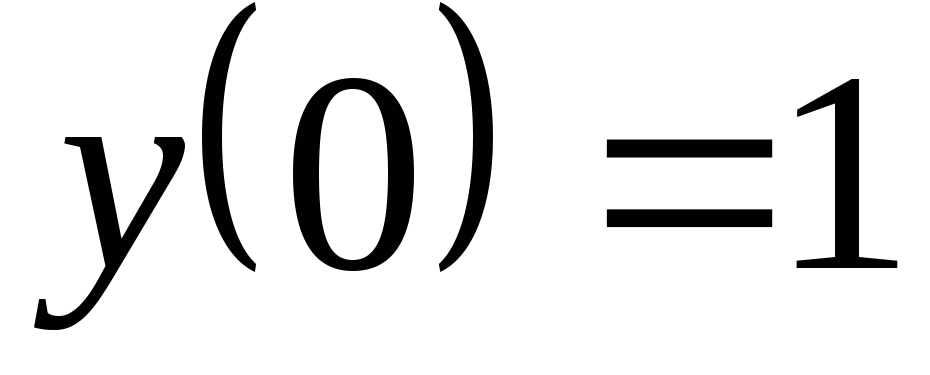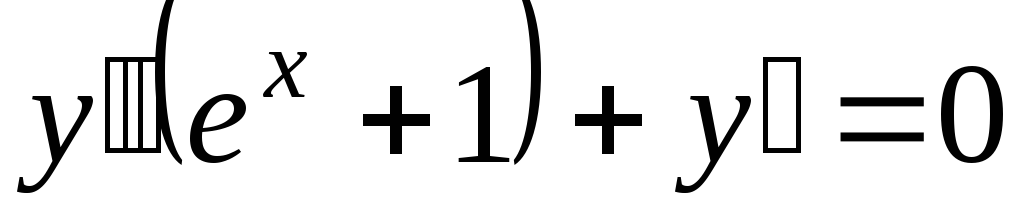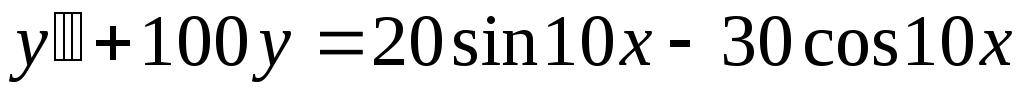10. ; ; .

Вариант 27

1. .

2. .

3. .

4. .

5. .

6. ; .

7. ; .

8. .

9. .

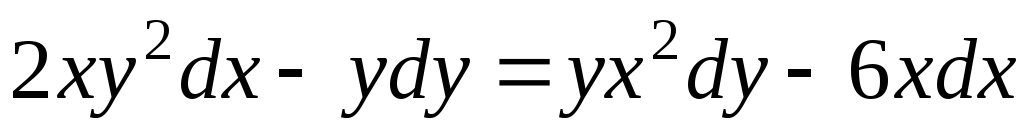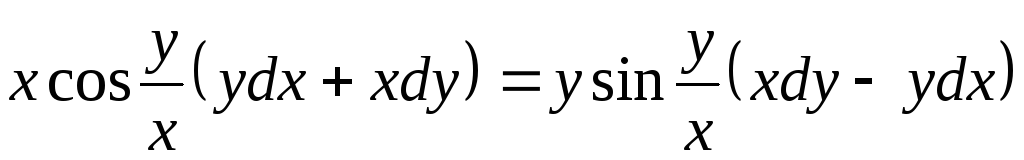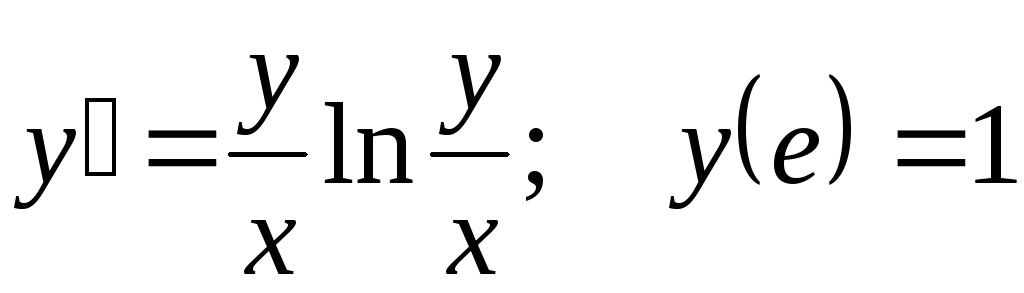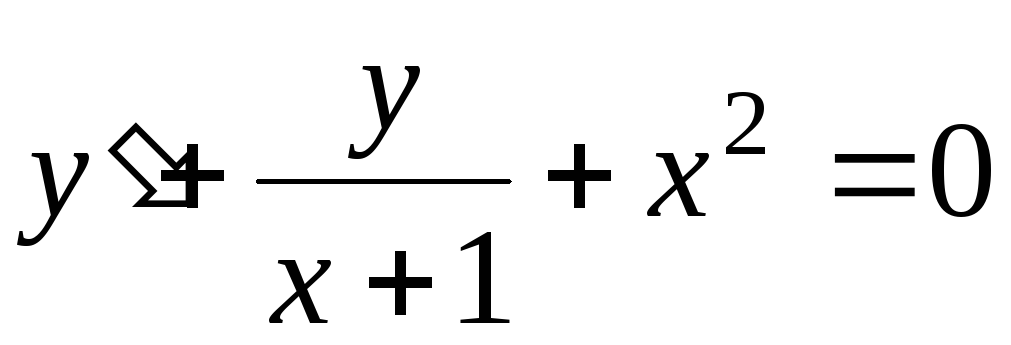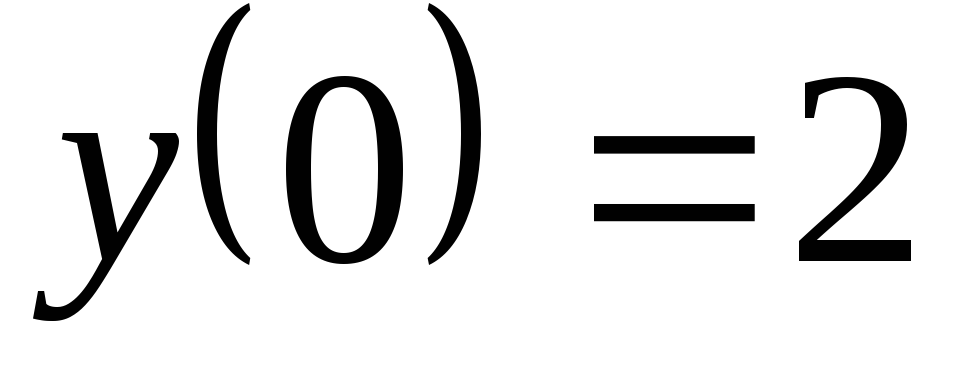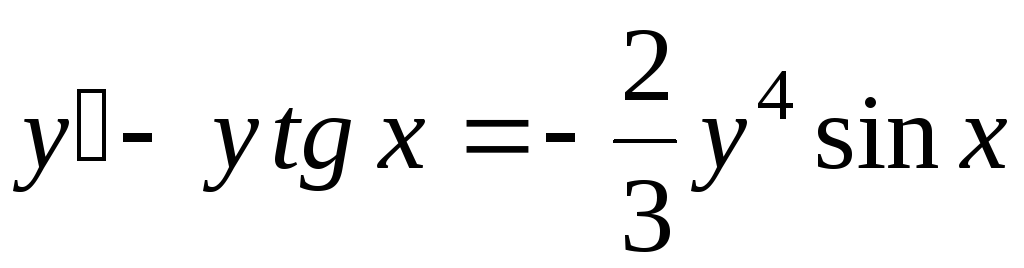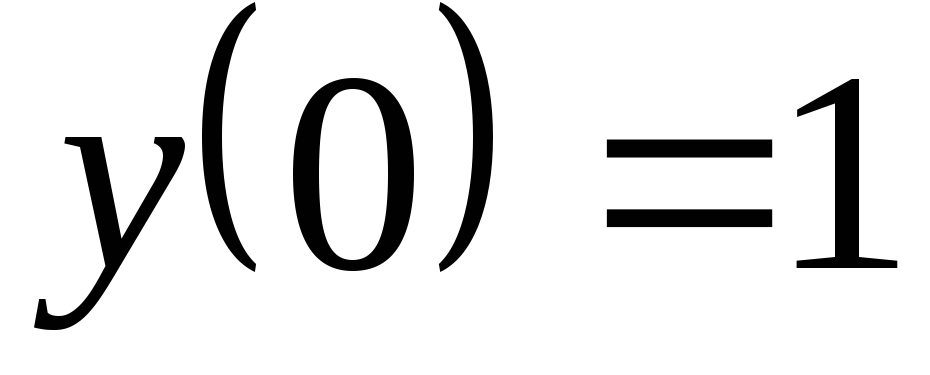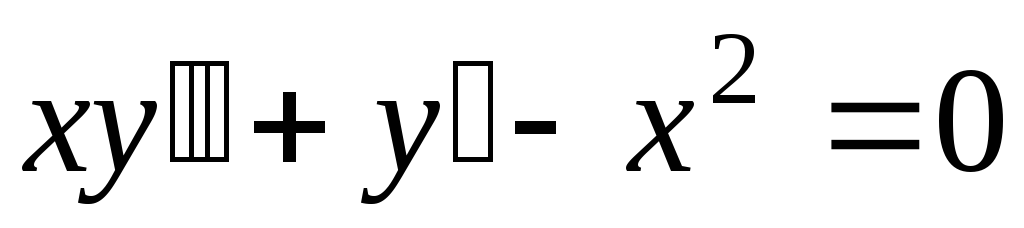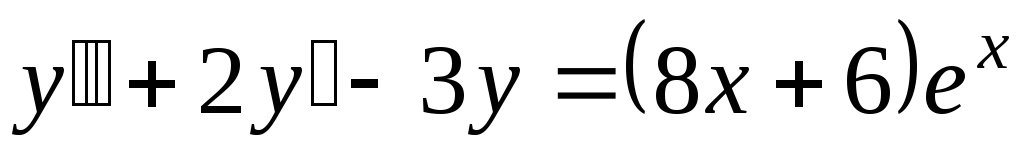10. ; ; .

Вариант 28

1. .

2. .

3. .

4. .

5. .

6. ; .

7. ; .

8. .

9. .

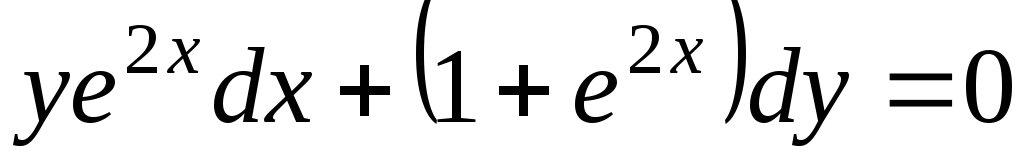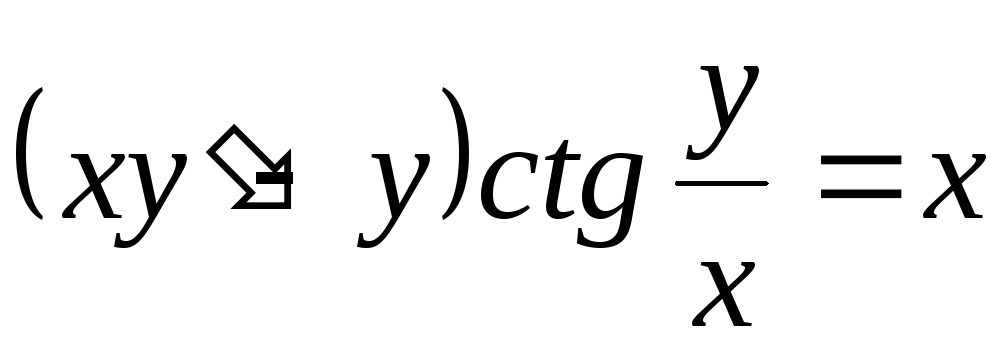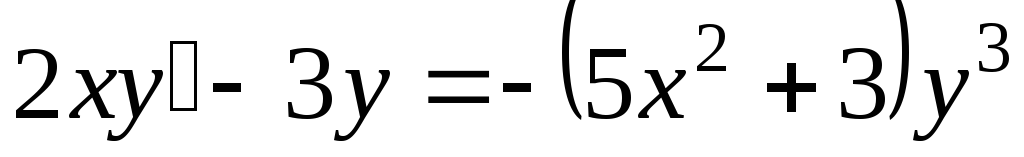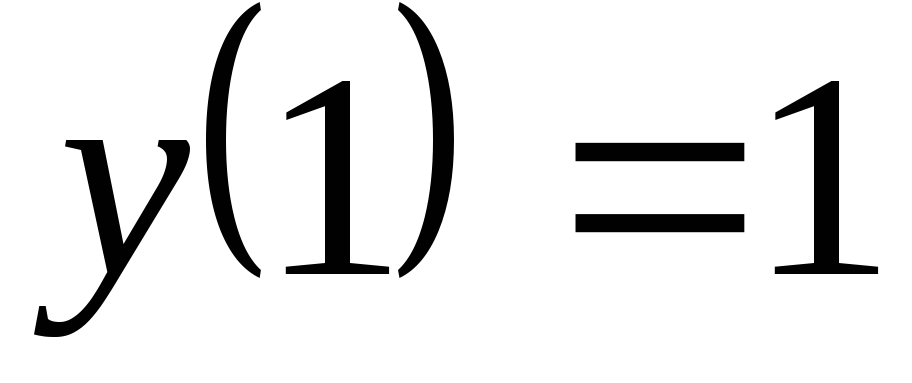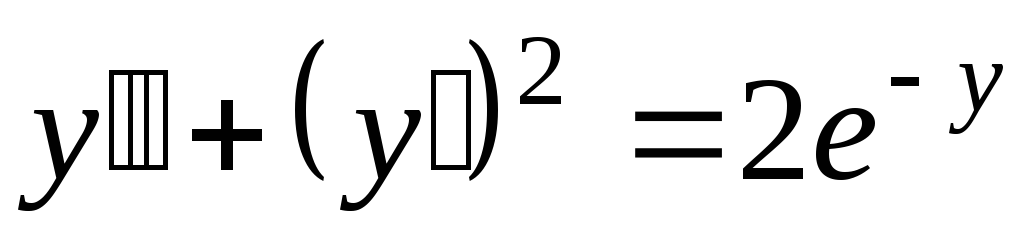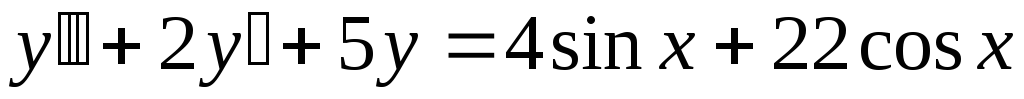10. ; ; .

Вариант 29

1. .

2. .

3. .

4. .

5. .

6. ; .

7. ; .

8. .

9. ; ;

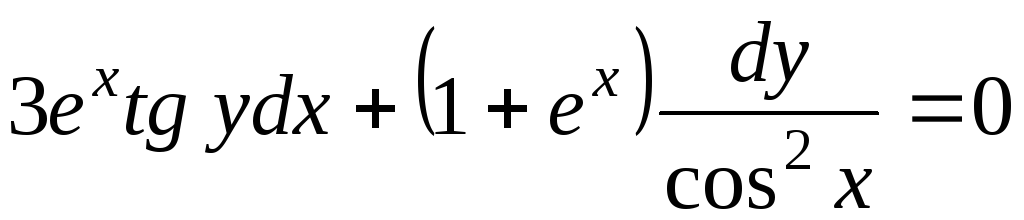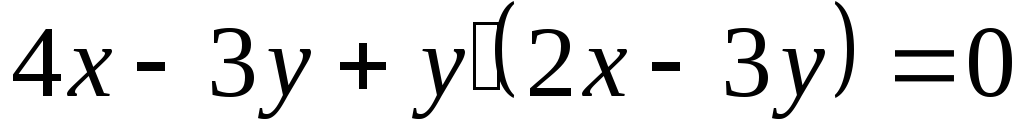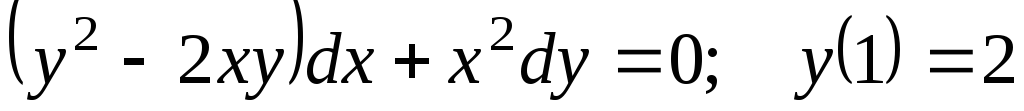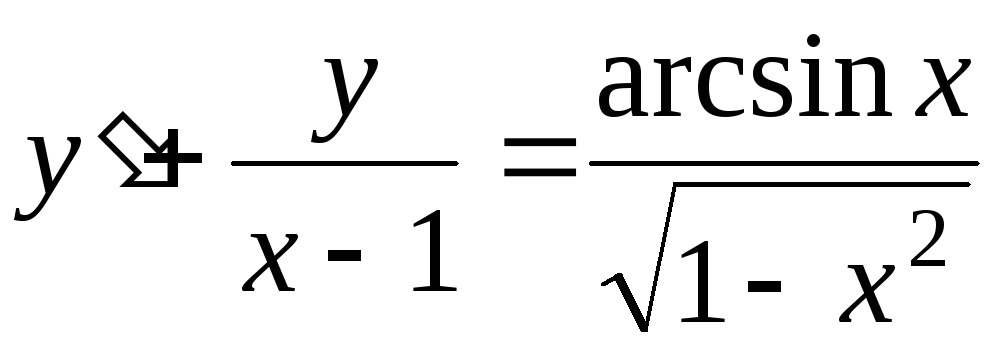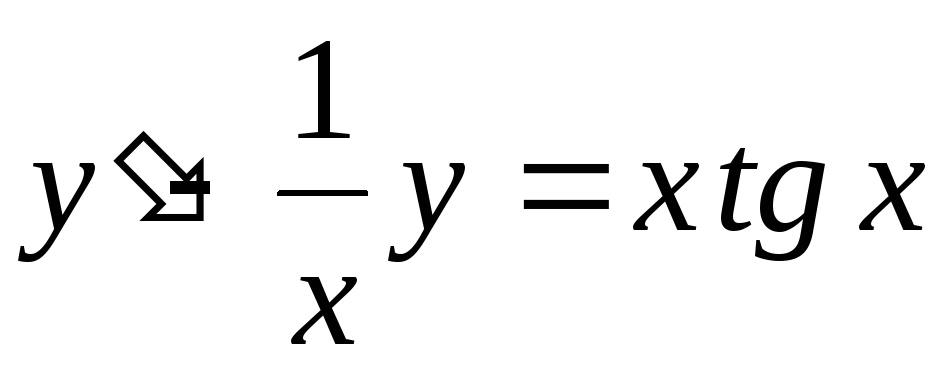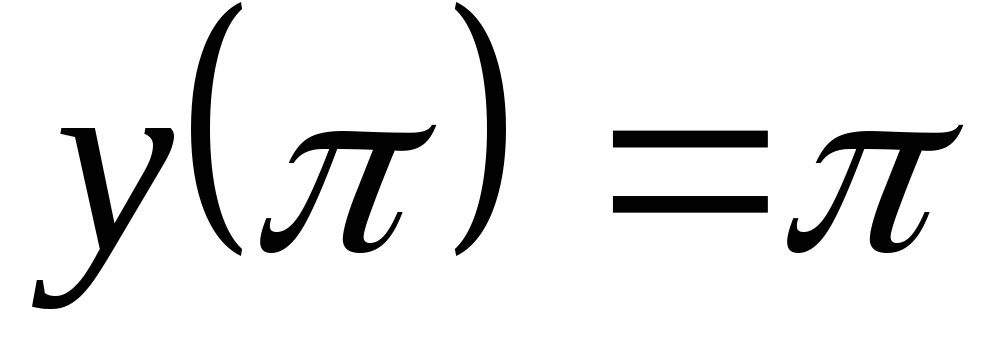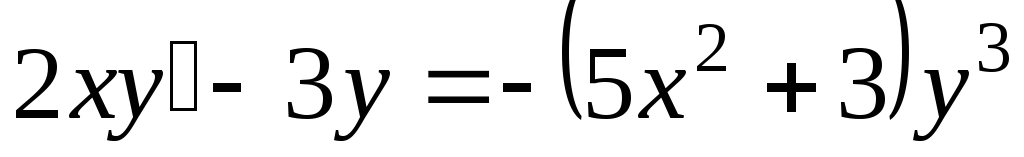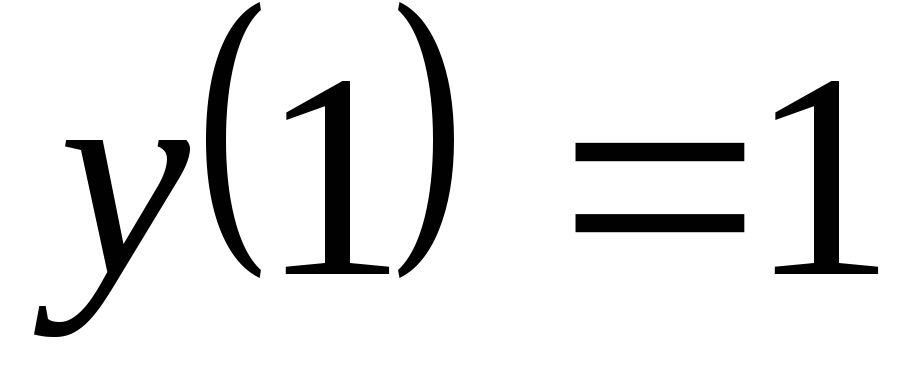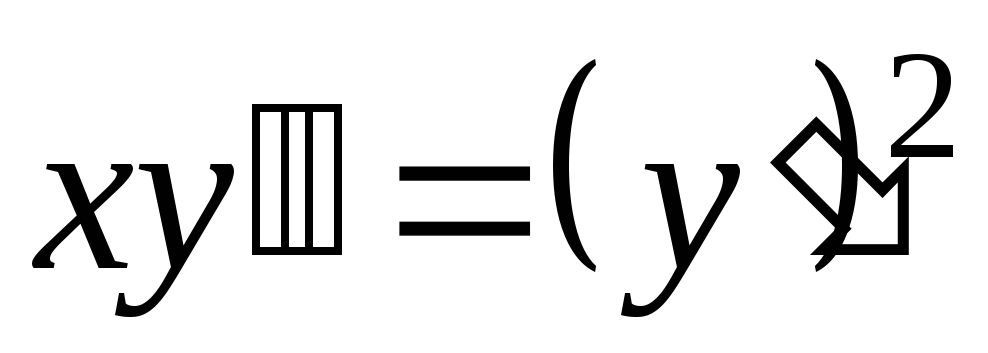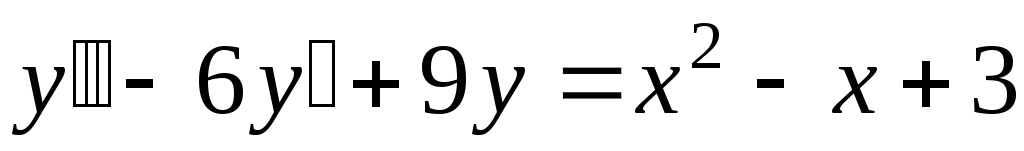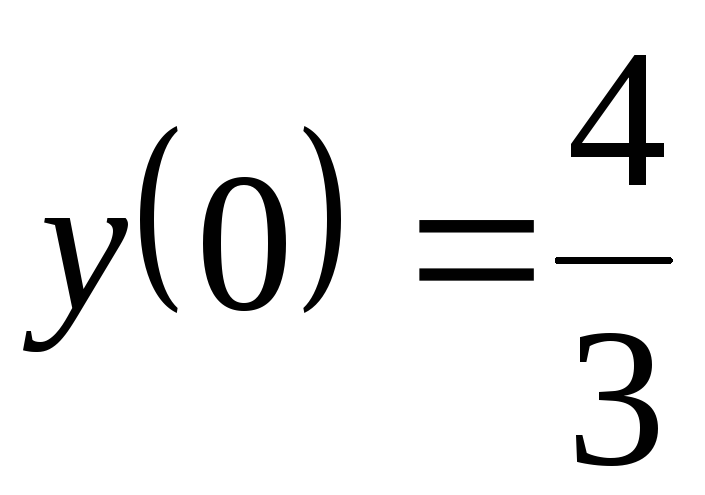10. ;

Вариант 30

1. .

2. .

3. .

4. .

5. .

6. ; .

7. ; .

8. .

9. .

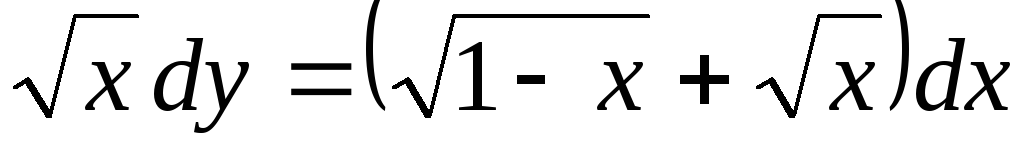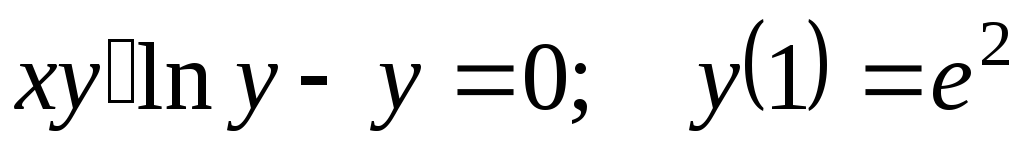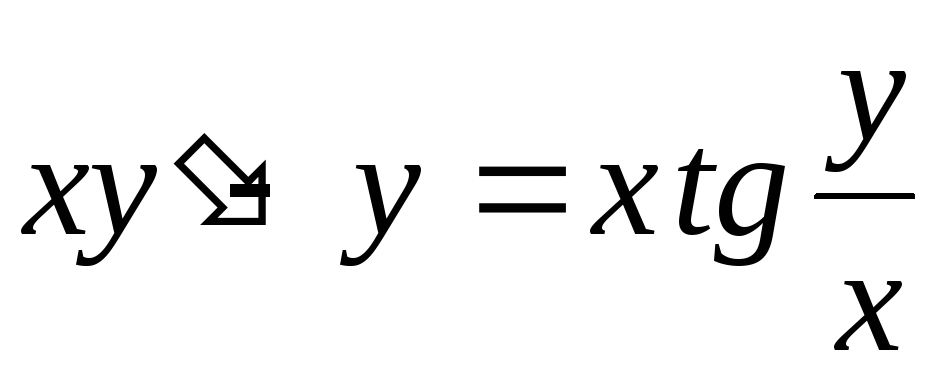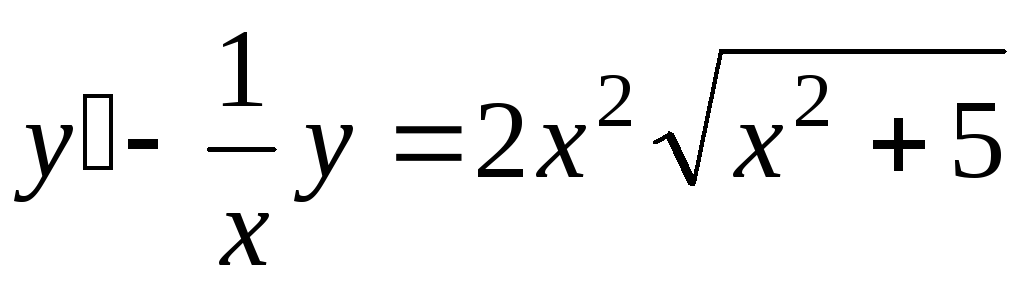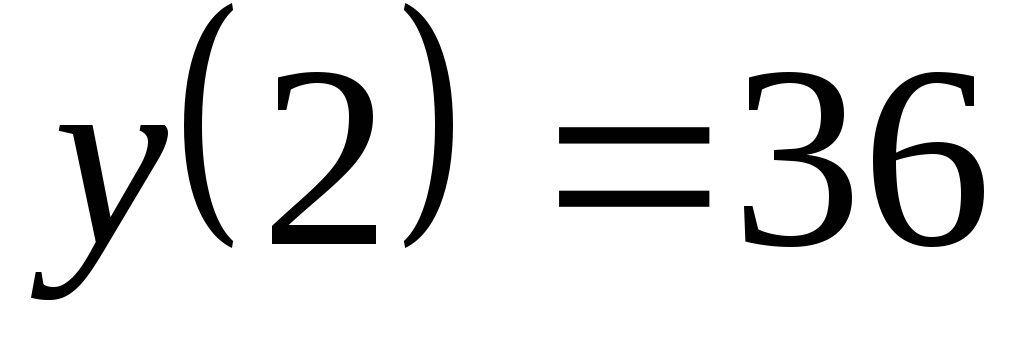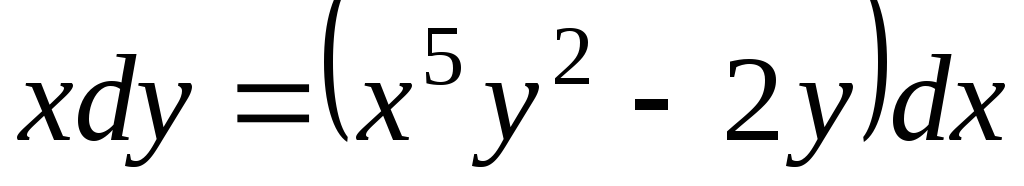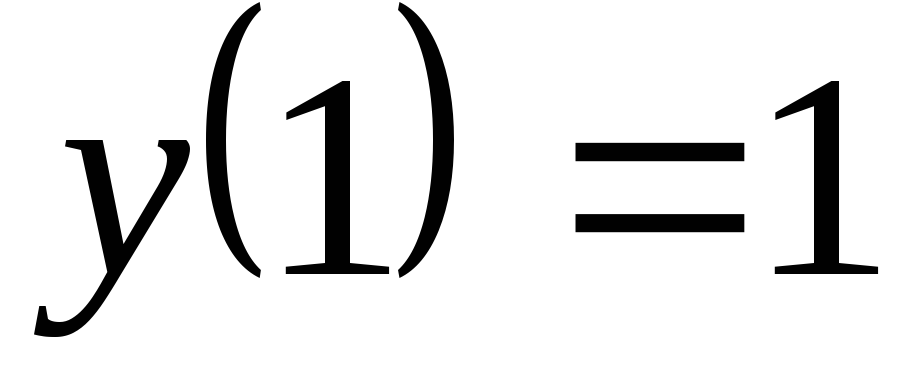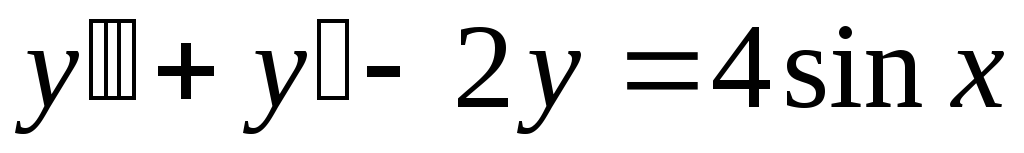10. ; .

Зразок виконання індивідуального завдання з теми

“Диференціальні рівняння”

Приклади індивідуального завдання містять диференціальні рівняння з відокремлюваними змінними (1, 2), однорідні рівняння (3, 4), лінійні диференціальні рівняння першого порядку (5, 6), рівняння Бернуллі (7) та диференціальні рівняння другого порядку (8, 9, 10). При розв’язанні обмежимося наведенням рішення одного диференціального рівняння кожного типу.

Приклад 1. Знайти частинний розв’язок диференціального рівняння , який задовольняє початковій умові .

Розв’язок. Це рівняння є диференціальним рівнянням з відокремлюваними змінними. Спочатку визначимо загальний розв’язок рівняння. Для цього розв’яжемо його відносно та замінимо на :

.

Відокремимо змінні: .

Після інтегрування маємо: .

Пропотенцюємо останній вираз: або – загальний розв’язок.

Використовуючи початкову умову , знаходимо значення довільної сталої :

.

Для отримання частинного розв’язку рівняння значення сталої підставимо у загальний розв’язок .

Приклад 2. Знайти частинний інтеграл диференціального рівняння , який задовольняє початковій умові .

Розв’язок. Згрупуємо доданки, які містять диференціали і :

.

Відокремити змінні неможливо завдяки наявності множника перед . Перейдемо від рівняння у диференціалах до рівняння в похідних. Для цього поділимо обидві частини рівняння на .

.

Поділивши тепер обидві частини рівняння на :

–

будемо мати рівняння, загальний вигляд якого – це загальний вигляд однорідного відносно змінних та рівняння. Для його розв’язання застосуємо заміну ; .

.

Після перемноження виразів у скобках та згрупування відповідним чином, отримаємо рівняння з відокремлюваними змінними:

.

Далі, як у попередньому прикладі, замінимо на , відокремимо змінні та інтегруємо для отримання загального розв’язка диференціального рівняння. Остаточно отримаємо:

.

Зробивши зворотну підстановку (замість підставимо ) і використавши властивості логарифмів, запишемо загальний інтеграл:

.

Зауважимо, що розв’язати отримане рівняння відносно неможливо.

Використовуючи початкову умову , отримаємо:

.

Остаточно маємо частинний інтеграл: .

Приклад 3. Розв’язати рівняння .

Розв’язок. Дане рівняння є лінійним неоднорідним диференціальним рівнянням першого порядку. Розв’яжемо його за допомогою методу Бернуллі.

Зробимо заміну . Тоді . Підставимо вирази для та в вихідне рівняння:

.

Згрупуємо члени рівняння, які містять , і винесемо за дужки

.

Нехай функція є частинним інтегралом рівняння . Тоді функція буде розв’язком рівняння . Розв’яжемо обидва рівняння, які є рівняннями з відокремлюваними змінними.

, ,

, ,

, ,

, ,

. .

Звідки остаточно отримаємо загальний розв’язок .

Зауваження: рівняння Бернуллі, загальний вигляд яких , також можна розв’язати методом Бернуллі, застосовуючи заміну .

Розв’язання диференціальних рівнянь другого порядку. Розглянемо деякі типи рівнянь, які допускають зниження порядку. Тобто такі рівнянні, які зводяться до диференціальних рівнянь першого порядку.

Приклад 4. Знайти частинний розв’язок рівняння , який задовольняє початковим умовам .

Розв’язок. Загальний вигляд рівнянь цього типу: . Загальний розв’язок знайдемо послідовним інтегруванням, кожного разу знижуючи порядок рівняння.

;

.

Для отримання частинного розв’язку скористаємося початковими умовами.

, .

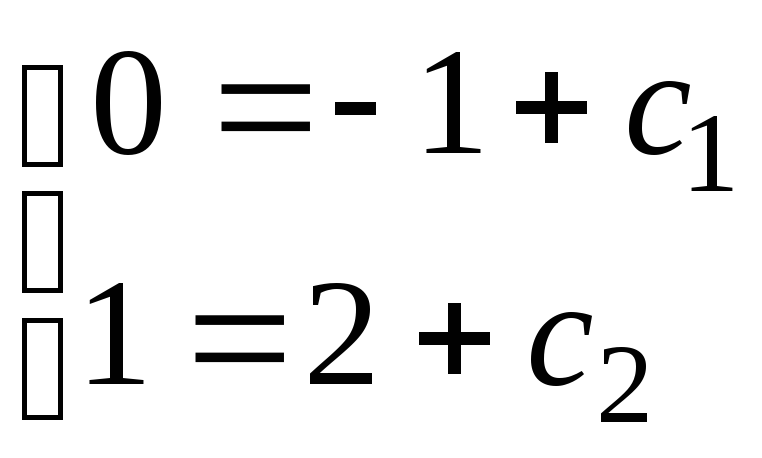Остаточно отримаємо: .

Приклад 5. Знайти загальний розв’язок рівняння .

Розв’язок. Це рівняння другого порядку, в якому у явному вигляді немає функції .Загальний вигляд таких рівнянь . Зробивши заміну , , отримаємо рівняння першого порядку відносно невідомої функції , розв’язавши яке із другого рівняння першого порядку знайдемо невідому функцію .

.

– загальний розв’язок.

Приклад 6. Знайти загальний розв’язок рівняння .

Розв’язок. Це рівняння другого порядку, в якому у явному вигляді немає , загальний вигляд таких рівнянь . Для розв’язання доцільно зробити заміну , тоді . Дане рівняння набуває вигляду:

.

Отримали рівняння першого порядку з відокремлюваними змінними. Розв’язуючи його відповідним методом, отримаємо:

,

.

Розв’яжемо друге рівняння першого порядку :

.

Відокремлюючи змінні та інтегруючи рівняння. знаходимо загальний розв’язок:

.

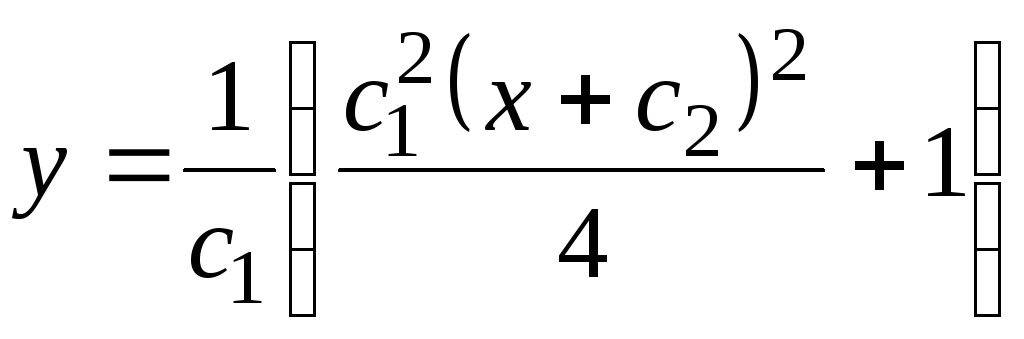Приклад 7. Знайти загальний розв’язок рівняння

.

Розв’язок. Це рівняння відноситься до неоднорідних рівнянь другого порядку зі сталими коефіцієнтами. Загальний розв’язок шукаємо у вигляді .

Знаходимо - загальний розв’язок однорідного рівняння . Для цього складемо характеристичне рівняння

.

Його корені . Отже , бо .

125