
- •Численные методы
- •2012 Введение
- •1. Решение нелинейных уравнений
- •Постановка задачи
- •1.2. Основные этапы отыскания решения
- •1.3. Метод половинного деления
- •1.4. Метод простой итерации
- •Приведение уравнения к видудля обеспечения выполнения неравенства
- •1.5. Метод Ньютона (метод касательных)
- •1.6. Видоизменённый метод Ньютона
- •1.7. Метод хорд
- •1.8. Комбинированный метод
- •Решение систем линейных алгебраических уравнений
- •2.1. Постановка задачи
- •2.2. Метод простой итерации
- •2.3. Метод Зейделя
- •3. Решение систем нелинейных уравнений
- •3.1. Постановка задачи
- •3.2. Метод Ньютона для системы нелинейных уравнений
- •3.3. Метод итерации для нелинейной системы уравнений
- •3.4. Метод скорейшего спуска решения нелинейных систем
- •3.5. Метод скорейшего спуска для случая линейной системы
- •4. Приближение функций
- •4. 1. Метод наименьших квадратов
- •4.2. Построение интерполяционных многочленов
- •Многочлен Лагранжа
- •Многочлен Ньютона с конечными разностями
- •5. Вычисление собственных значений матрицы Методом Данилевского
- •6. Вычисление определённых интегралов. Метод симпсона (метод парабол)
- •7. Численное решение дифференциальных уравнений
- •7.1. Постановка задачи Коши
- •7.2. Метод Эйлера
- •7.3. Модифицированные методы Эйлера
- •7.4. Метод Рунге – Кутта
- •Решение краевой задачи для линейного дифференциального уравнения второго порядка методом прогонки
5. Вычисление собственных значений матрицы Методом Данилевского
Сущность метода Данилевского заключается в том, что исходная матрица А:

после
![]() преобразования подобия приводится к
матрице Фробениуса Р:
преобразования подобия приводится к
матрице Фробениуса Р:
 ,
,
то
есть
![]() , где
, где![]() – неособенная матрица. Так как подобные
матрицы обладают одинаковыми
характеристическими полиномами, то
имеем:
– неособенная матрица. Так как подобные
матрицы обладают одинаковыми
характеристическими полиномами, то
имеем:
![]() .
.
Вначале
нужно строку
![]() привести в строку
привести в строку
![]() .Предполагая,
что
.Предполагая,
что
![]() ,
разделим все элементы
,
разделим все элементы![]() – го столбца матрицы А на
– го столбца матрицы А на![]() .
Тогда её
.
Тогда её![]() -ая
строка примет вид
-ая
строка примет вид
![]() .
.
Затем
вычтем
![]() -
й столбец преобразованной матрицы,
умноженный соответственно на числа
-
й столбец преобразованной матрицы,
умноженный соответственно на числа![]() ,
из всех остальных ее столбцов.
,
из всех остальных ее столбцов.
В результате получим матрицу, последняя строка которой имеет желаемый вид 0 0 … 1 0.
Произведя те же операции над единичной матрицей, получим матрицу
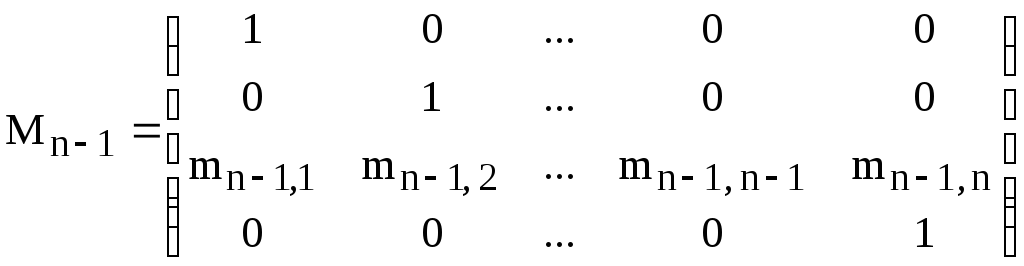 ,
,
где
![]() при
при![]() .
(1)
.
(1)
![]() .
(1')
.
(1')
Эти
операции равносильны умножению справа
матрицы
![]() на матрицу А.
на матрицу А.
 ,
(2)
,
(2)
где
![]() при
при![]() ,
,
![]() при
при
![]() .
(2')
.
(2')
Для
подобия матриц нужно умножить полученную
матрицу на
![]() слева:
слева:![]() .
.
Очевидно, обратная матрица имеет вид
 .
.
Обозначим
![]() ,
то есть
,
то есть
 ,
,
где
![]() (3)
(3)
![]() при
при
![]() ,
(3')
,
(3')
то есть полученная матрица С подобна матрице А.
Продолжая этот процесс, получим матрицу Фробениуса.
![]() ,
,
если
все
![]() промежуточных преобразований возможны.
промежуточных преобразований возможны.
Пример. Привести к виду Фробениуса матрицу:
 .
.
Решение.
Вычисления
будем располагать в таблице 4. В строках
1–4 помещаем элементы
![]() данной матрицы и контрольные суммы
данной матрицы и контрольные суммы![]() в
в![]() .
Элемент
.
Элемент![]() .
В строкеI
записываем элементы третьей строки
матрицы
.
В строкеI
записываем элементы третьей строки
матрицы
![]() ,
вычисляемые по формулам (1), (1'):
,
вычисляемые по формулам (1), (1'):
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Сюда
же помещаем элемент
![]() .
Число -3,375 должно совпасть с элементами
строкиI
, не входящими в контрольный столбец
(после замены элемента
.
Число -3,375 должно совпасть с элементами
строкиI
, не входящими в контрольный столбец
(после замены элемента
![]() на -1).
на -1).
В
строках 5–8 в графе
![]() выписываем третью строку матрицы
выписываем третью строку матрицы![]() ,
которая совпадает с четвертой строкой
исходной матрицы А. В строках 5–8 в
соответствующих столбцах выписываем
элементы матрицы
,
которая совпадает с четвертой строкой
исходной матрицы А. В строках 5–8 в
соответствующих столбцах выписываем
элементы матрицы![]() ,
вычисляемые по формулам (2), (2'):
,
вычисляемые по формулам (2), (2'):
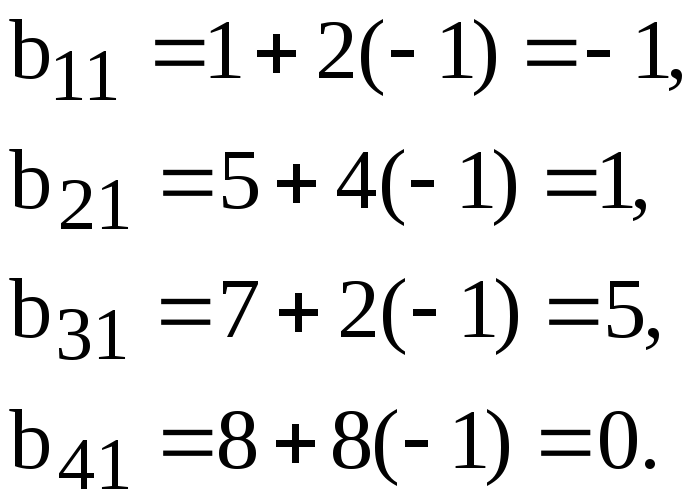
Преобразованные
элементы третьего столбца получаются
с помощью умножения исходных элементов
на
![]() .
Например,
.
Например,
![]()
Таблица 4
|
Номер строки |
|
Столбцы матрицы |
Σ |
Σ/ | |||
|
1 |
2 |
3 |
4 | ||||
|
1 |
|
1 |
3 |
2 |
4 |
10 |
|
|
2 |
|
5 |
9 |
4 |
1 |
19 | |
|
3 |
|
7 |
3 |
2 |
6 |
18 | |
|
4
|
|
8 |
7 |
8 |
4 |
27 | |
|
I |
|
-1 |
-0,875 |
0 -1 |
-0,5 |
-3,375 | |
|
5 |
8 |
-1 |
1,25 |
0,25 |
3 |
3,5 |
3,25 |
|
6 |
7
|
1 |
5,5 |
0,5 |
-1 |
6,0 |
5,5
11,25 |
|
7 |
8 |
5 |
1,25 |
0,25 |
5 |
1 | |
|
8 |
4 |
0 |
0 |
1 |
0 |
1 |
0 |
|
7/ |
|
39 |
58,5
|
11,5 |
57 |
166 |
|
|
II |
|
-0,67 |
0,017 -1 |
-0,127 |
-0,97 |
-2,83 |
|
|
9 |
39 |
-1,8333 |
0,021 |
0,004 |
1,782 |
-0,026 |
-0,047 |
|
1 |
58,5 |
-2,666 |
0,094 |
-0,5811 |
-6,3589 |
-9,512 |
-9,606 |
|
11 |
11,5 |
0 |
1 |
0 |
0 |
1 |
0 |
|
12 |
57 |
0 |
0 |
1 |
0 |
1 |
1 |
|
10/ |
|
- |
17,818 |
23,16165 |
-302,4 |
-488,966 |
|
|
III |
|
0,0044 1 |
0,0783 |
0,1 |
-1,3298 |
-2,14 |
|
|
13
|
-227,45 |
0,008 |
-0,1226 |
-0,1827 |
4,22 |
3,9228 |
3,91148 |
|
17,818 |
1 |
0 |
0 |
0 |
1 |
0 | |
|
23,16165 |
0 |
1 |
0 |
0 |
1 |
1 | |
|
-302,497 |
0 |
0 |
1 |
0 |
1 |
1 | |
|
|
|
16 |
51 |
-261 |
-960 |
|
|
Соответственно, последняя строка матрицы В имеет вид (0 0 1 0). Для контроля пополним матрицу В преобразованными по аналогии элементами:
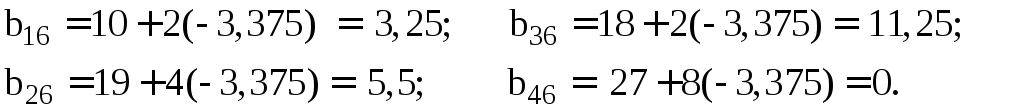
Полученные результаты записываем в столбце Σ/ . Прибавив к ним элементы третьего столбца, будем иметь контрольные суммы:
![]() для строк 5–8
(столбец Σ) .
для строк 5–8
(столбец Σ) .
Преобразование
![]() , произведенное над матрицей В и дающее
матрицу
, произведенное над матрицей В и дающее
матрицу![]() ,
изменяет лишь третью строку матрицы В,
то есть седьмую строку таблицы. Элементы
строки
,
изменяет лишь третью строку матрицы В,
то есть седьмую строку таблицы. Элементы
строки![]() получаются по формулам (3), (
получаются по формулам (3), (![]() )
. Например:
)
. Например:
![]() .
.
Те же преобразования проводим над столбцом Σ:
![]() .
.
В
результате получаем матрицу С, состоящую
из строк 5, 6,
![]() , 8 с контрольными суммами Σ. Далее, приняв
матрицу С за исходную и выделив элемент
, 8 с контрольными суммами Σ. Далее, приняв
матрицу С за исходную и выделив элемент![]() ,
продолжим процесс аналогичным образом.
,
продолжим процесс аналогичным образом.
Таким образом, матрица Фробениуса имеет вид

Отсюда,
решая уравнение
![]() ,
найдем собственные значения исходной
матрицы.
,
найдем собственные значения исходной
матрицы.



 ,125
,125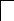
 1,5
1,5

 0
0 227,4597
227,4597
