Динамический хаос (ИПИС, ФКС)

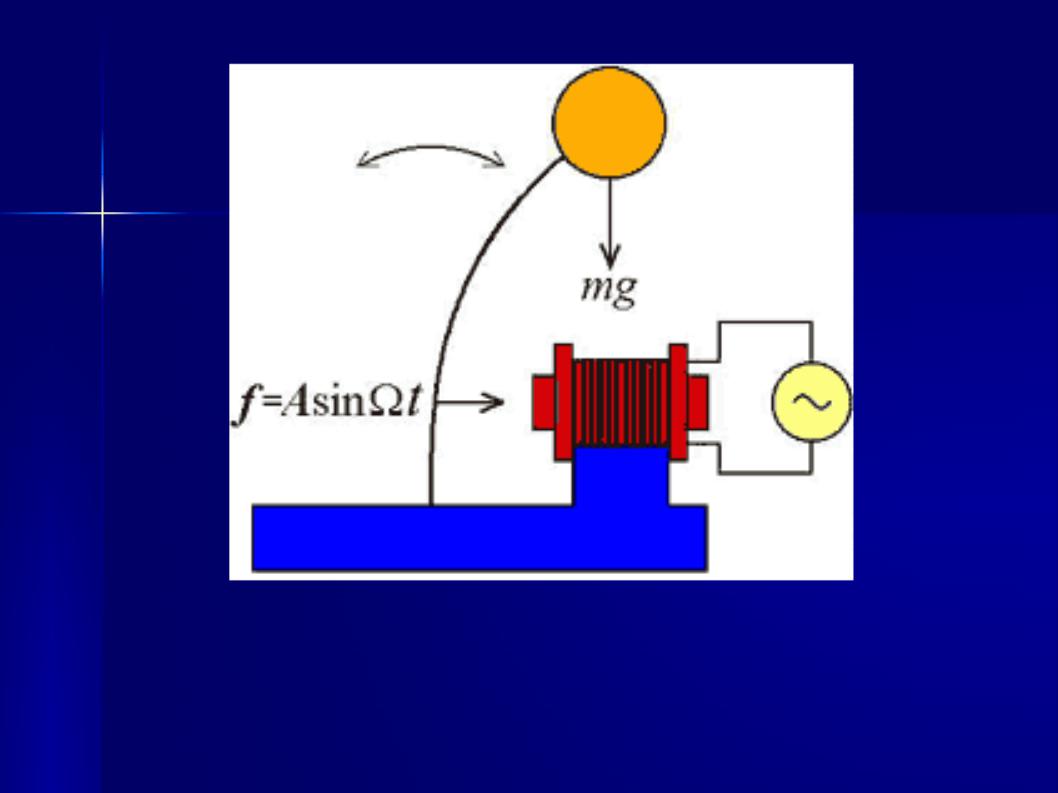
Рис. 88. Осциллятор Уэды под внешним периодическим воздействием.

Устройство состоит из шарика, закреплённого на вертикальной упругой пластине, коэффициент упругости которой подобран так, что при малых углах отклонения возвращающая сила упругости в точности компенсирует отклоняющий момент силы тяжести. Осциллятор Уэды может быть реализован также в виде электрической схемы – колебательного контура с нелинейной индуктивностью.

Для описания движения осциллятора Уэды преобразуем

уравнение	(195),		введя новые безразмерные		переменные
t и	X	x . В результате получим
				a sin( t) ,
		x x x3
				Asin( ) ,
		X X X 3			(197)
где введены		параметры A a 3 ,			, которые
характеризуют амплитуду и частоту воздействия,
соответственно.

Уравнение (197) можно переписать в виде системы

	X Y
	.	(198)
Y	X 3 Y Asin( )

Используя формулу (136), можно определить, является ли система (198) диссипативной. Согласно (136),

dV			divF dV		N	F	dV
						i		.
dt						x
		V		V	i 1	i

В нашем случае x {X ,Y}, а F {Y, X 3 Y Asin( )}. Тогда дивергенция поля F будет равна

div F	FX		FY	0 1 1	.
	X		Y

Значит, фазовый объём V будет меняться по закону

dVdt V ,

V V0 exp( ) .

Значит, рассматриваемая система (198) является диссипативной, поэтому с течением времени все фазовые траектории системы должны приближаться к некоторому аттрактору.

Анализ уравнения (197) показывает, что при малой амплитуде A частота колебаний системы будет совпадать с частотой внешнего воздействия, а при увеличении параметра A можно наблюдать более сложное динамическое поведение, включая переход к хаосу. В этом случае система будет обладать странным аттрактором – аттрактором Уэды.

Поскольку функция f (x) x3– нечётная, уравнение движения (197) обладает симметрией – оно инвариантно относительно одновременной замены X X и . Поэтому всегда реализуется одна из двух возможностей:

1)аттрактор обладает симметрией относительно указанной замены;

2)аттрактор не обладает симметрией, но имеет симметричного партнёра, т.е. в зависимости от начальных условий в системе будут возникать два разных установившихся режима, переходящие один в другой при преобразовании симметрии.

На рис. 89 показана карта динамических режимов осциллятора Уэды на плоскости параметров ( , A) . По периферии рисунка приводятся фазовые портреты аттрактора в проекции на плоскость переменных ( X ,Y ) ( X , X ), дающие представления об эволюции аттрактора в зависимости от параметров.

Зелёным цветом отмечены области с периодом, равным периоду воздействия, жёлтым – области с удвоенным периодом, розовым – отношение периодов 3, синий – 4, красный – 8. Серым цветом обозначен хаос.

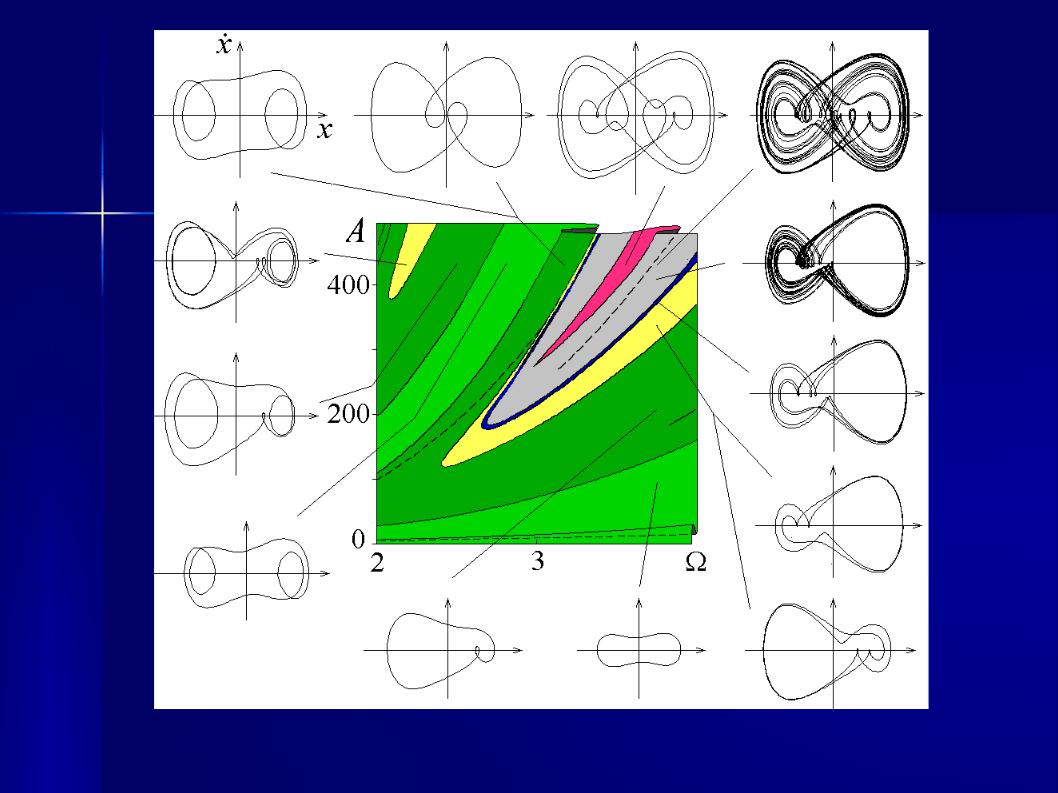
Рис. 89. Карта динамических режимов осциллятора Уэды.

Из рис. 89 видно, что при малой амплитуде A единственным аттрактором является замкнутая кривая – симметричный цикл, причём период колебаний системы при этом равен периоду внешнего воздействия. При увеличении амплитуды можно наблюдать бифуркацию потери симметрии. Она состоит в том, что симметричный цикл становится неустойчивым и возникают два цикла-аттрактора. В частности два фазовых портрета в правом нижнем углу рисунка соответствуют двум взаимно симметричным аттракторам, сосуществующим в одной и той же точке плоскости параметров. Далее, на базе каждого из асимметричных циклов наблюдается каскад бифуркаций удвоения периода, завершающийся переходом к хаосу. При этом пока амплитуда не очень велика сосуществуют два асимметричных хаотических аттрактора. При большой же амплитуде воздействия они сливаются в один симметричный хаотический аттрактор.