2.матан.интегралы / ПоверхностныеИнт / ТеоремаСтокса

Теорема Стокса

Пусть S является гладкой поверхностью, ограниченной гладкой кривой C. Тогда для любой непрерывно дифференцируемой векторной функции

справедлива теорема Стокса

где векторное произведение дивергенции векторного поля на вектор F

− это ротор векторного поля 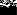. Символ показывает, что криволинейный интеграл вычисляется по замкнутой кривой. Будем предполагать, что ориентация поверхности и направление обхода кривой соответствуют правилу правой руки. В этом случае при обходе кривой поверхность всегда остается слева, если голова направлена в ту же сторону, что и вектор нормали .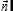

Теорема Стокса связывает между собой криволинейные интегралы второго рода и поверхностные интегралы второго рода.

Если поверхность S задана в д.с.к. и однозначно проектируется на каждую из координатных плоскостей, то она называется xyz – проектрируемой. Для такой поверхности, если она расположена внутри области, где функции P, Q, R имеют непрерывные частные производные первого порядка, теорема Стокса может быть записана в координатной форме

Пример.

Показать, что данный криволинейный интеграл равен нулю вдоль любого замкнутого контура C. Решение. Обозначим через S поверхность, ограниченную замкнутой кривой C. Применяя формулу Стокса, можем записать

Тогда ротор векторного поля равен

Следовательно, находим значение криволинейного интеграла

Утверждение доказано.