Многоэлектронный атом

21

Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции, записанной через орбитали (орбитальное приближение). Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений.

Хотя электроны неразличимы, в орбитальном приближении каждый электрон описывается "своей" волновой функцией. Системы, в которых все электроны занимают орбитали попарно, называются системами с закрытыми (замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами орбиталей, число которых равно половине числа электронов. Системы с нечетным числом электронов называются системами с открытыми (незамкнутыми) оболочками.

9. Метод Хартри-Фока

Аппроксимация многоэлектронной волновой функции единственным детерминантом Слейтера (64) и использование при ее нахождении приближения самосогласованного поля приводят к методу Хартри-Фока (ХФ). При этом исходное электронное уравнение Шредингера (21) путем довольно громоздких математических вычислений преобразуется в уравнение, где точный гамильтониан H (34) заменен оператором Фока (фокианом):

1

N

N

Z

N

N

2 1

1

1

Fi = −

∑ i2

−∑

+ ∑∑

∫

χj (xj )

dxj −

∫

χi* (xj )

χj (xj )dxj . (65)

2

r

x

2

x

i

i

i

j

i

ij

ij

Здесь и далее мы используем принятую в квантовой химии атомную систему единиц: множитель

1/(4πε0 ) опускается, m = 1, e = 1, ħ =1. Введение атомных единиц делает формулы менее громоздкими.

Различие между F и H состоит в том, что оператор кулоновского электронного взаимодействия

n	n		e2
∑∑							заменен в (65) оператором в квадратных скобках, описывающим взаимодействие ка-
			4πε		r
i	j			0			i, j
					ij

ждого электрона со средним полем всех остальных электронов с учетом требований принципа Паули. Из ус-

ловия минимума энергии Ψ|F|Ψ возникает набор независимых уравнений для каждой одноэлектронной

орбитали – уравнений Хартри-Фока:

N 2 hi (xi )χi (xi )+∑ ∫χj (xj)

j=1

1

1

∫

*

1

dx

χ

(x )−

χ

(x )

χ

(x )dx

r−1

2

j

i

i

j

j

r−1 i

j j

ij

ij

	χ			=ε χ	(x )
		(x )				. (66)
	j	i		i i	i

Энергия электрона, находящегося на орбитали χi , может быть получена умножением слева выражения (66)

на χi и интегрированием по всему пространству:

N	1 Kij ) ,
еi = hii +∑(Jij −		(67)
j=1	2
Здесь
hii = ∫χi* (xi )hi χi (xi )dxi ,		(68)

				1				22
Jij	= ∫χi* (xi )χi* (xi )					χj (x j )χj (x j )dxi dx j ,		(69)
				rij
Kij	= ∫	χi* (xi )χ*j (xi	)		1		χi (x j )χj (x j )dxi dx j .	(70)
					rij
Одноэлектронный интеграл		hii описывает энергию электрона на орбитали чi						в поле ядра без осталь-

ных электронов. Двухэлектронный кулоновский интеграл Jij описывает энергию межэлектронного отталкива-

ния при независимом движении электронов. Двухэлектронный обменный интеграл Kij отражает понижение

энергии взаимодействия электронов с параллельными спинами на орбиталях χi и χj .

Полная энергия атома с замкнутыми электронными оболочками (по 2 электрона на каждой орбитали) в методе ХФ вычисляется следующим образом:

N	N	N
E = 2∑εi −∑∑(2Jij −Kij ) .			(71)
1=1	i=1	j=1

Подчеркнем, что оператор Фока (65) сам зависит от полного набора одноэлектронных волновых функций и его решение ищется самосогласованно. По этой причине метод ХФ иногда отождествляют с методом ССП. Поскольку, однако, общая стратегия самосогласования проявляется в квантовой химии во многих контекстах, название "метод Хартри-Фока" более точное.

Наличие обменного члена в операторе Фока эквивалентно учету корреляции в движении электронов с одинаковыми спинами, связанных с разными орбиталями (обменной корреляции). Кулоновская корреляция, вызванная взаимным отталкиванием электронов независимо от их спинов, в методе ХФ не учитывается: это является следствием приближения независимых частиц и представляет собой существенный недостаток метода.

Уравнения ХФ могут в принципе быть решены численно любым стандартным методом решения инте- грально-дифференциальных уравнений.

10. Ограниченный и неограниченный методы Хартри-Фока

Многоэлектронная волновая функция N-электронной системы должна быть антисимметричной и отвечать определенным проекциям N-электрон-ных орбитального углового и спинового моментов. Она также будет собственной функцией оператора квадрата полного спина системы S2, если она построена из пространственных спин-орбиталей, занятых парой электронов с противоположными спинами. Когда волновая функция аппроксимируется единственным детерминантом Слейтера, состоящим из таких спин-орбиталей, метод называется ограниченным (по спину) методом Хартри-Фока (ОХФ). Если же требование быть собственной функцией S2 на волновую функцию не накладывается, метод называется неограниченным методом ХФ (НХФ), и электроны с противоположными спинами занимают разные АО (рис. 9). В последнем случае достигается большая гибкость волновой функции. НХФ, как правило, применяется для систем с открытыми оболочками, обеспечивая для них более низкое значение энергии.

23

Энергия

Ψ(Li)= ϕ(1s)αϕ(1s)βϕ(2s)α

Рис. 9. Волновая функция атома Li в ограниченном и неограниченном методе Хартри-Фока

Таблица 5

Собственные значения квадрата спинового момента электронов для разных спиновых состояний

	Спиновое	Спин	Собственное зна-	Спиновое	Спин	Собственное зна-
	состояние		чение S2	состояние		чение S2
	Синглет	0	0	Квартет	1.5	3.75
	Дуплет	0.5	0.75	Квинтет	2	6.0
	Триплет	1	2.0	"N-тет"	N −1	s(s+1)
					2

Например, энергия дублетного спинового состояния молекулы CH3, рассчитанная ОХФ равна –39.555 a.е. при S2 = 0.750, тогда как расчет НХФ дает –39.559 a.е. при S2 = 0.761 (табл. 5). Говорят, что волновая функция НХФ не соответствует чистому спиновому состоянию. Степень чистоты спинового состояния оценивается по величине квадрата полного спина системы S2, которая должно быть равна s(s+1).

Из-за снятия фундаментального требования быть собственной функцией оператора S2 в больших системах иногда получают НХФ-решения с более низкой энергией и с собственными значениями S2, завышенными более чем на 10% по сравнению с истинными. Решения, у которых симметрия по спину понижена, называются "НХФ-нестабильными". Такая нестабильность указывает на непригодность описания волновой функции единственным детерминантом. Заметим, однако, что свойства ОХФ-решения часто точны даже в присутствии большой НХФ-нестабильности.

11. Метод Кона-Шэма

Многоэлектронная волновая функция Ψ({x}) связана с электронной плотностью (ЭП) основного состоя-

ния ρ(r) соотношением:

ρ(r=r1) = |e| ∫∫..∫∫∫ Ψ*({x})Ψ({x})dr2dr3…ds1ds2ds3… (72) r2 r3 s1 s2 s3

24

Интегрирование в (72) проводится по пространственным координатам всех электронов, кроме одного, и по спинам всех электронов. Поскольку электроны неразличимы, ρ(r) есть средняя по системе плотность электронов.

Электронная энергия системы зависит от ρ(r) следующим образом:

E[ρ] =	∫	VЯД (r)ρ(r)dV +	1	∫∫	ρ(r)ρ(			r')		drdr′+G[ρ] ,	(73)
			2				r −r'

где Vяд(r) – потенциал ядра, а G[ρ] – функционал ЭП, представляющий собой сумму кинетической энергии и

неклассической энергии электрон-электронного взаимодействия Exc[ρ], связанной с обменом и корреляцией электронов. Теорема Хоэнберга-Кона утверждает, что G[ρ] – одинаковый для всех многоэлектронных систем (универсальный) функционал электронной плотности, причем, точная ЭП основного состояния обеспечивает минимум функционала (73). Теория, которая изучает способы расчета электронной структуры молекул и кристаллов, основываясь на минимизации функционала (73), называется теорией функционала плотности (ТФП).

Предположим, что ЭП основного состояния взаимодействующих и невзаимодействующих электронов одинаковы. Выражение для кинетической энергии электронов (7) одинаково для всех систем. Тогда минимиза-

ция функционала (73) относительно одноэлектронных функций χi(r) при дополнительном условии их ортонормировки и постоянства числа электронов в системе дает одноэлектронные уравнения Кона-Шэма:

1

′

−

2 +V(r) +

ρ(r )

dr′+υˆ

(r)

χ

(r) =ε

χ

(r)

i=1,2,3,…

(74)

∫

,

2

r −r′

xc

i

i

i

где ρ = ∑ χi

2, V(r) – электростатический потенциал, создаваемый ядром, υˆxc (r) =

δExc[ρ]

– обменно-

δρ

i

корреляционный потенциал, Exc[ρ] – обменно-корреляционная энергия, зависящая от электронной плотности. Система уравнений (74) решается методом самосогласованного поля и заменяет в теории функционала плотности одноэлектронные уравнения Хартри-Фока. Все приближения связаны со способами аппроксимации обменно–корреляционного потенциала υˆxc (r) : поиск таких приближений составляет важный раздел теории

функционала плотности.

Энергии одноэлектронных состояний в теории функционала плотности равны

εi (ТФП) =	δE[ρ]	,	(75)
	δni

(ni – электронная заселенность состояния i), тогда как в методе Хартри-Фока они равны разности энергий двух состояний с числом электронов, отличающимся на единицу:

εi(ХФ) = EХФ, n	i	=1	– EХФ, n = 0 .	(76)
			i

Таким образом, решения одноэлектронных уравнений Кона-Шэма, вообще говоря, отличны от решений, полученных методом Хартри-Фока. Это иногда дает преимущество теории функционала плотности. Например, разложив энергию (76) в ряд Тейлора и приняв во внимание соотношение (75), можно получить для потенциала ионизации достаточно точное выражение

25

	Ii ≈ – εi(ni =	1	).	(77)
		2

Можно сказать, что потенциал ионизации может быть вычислен с помощью некоего переходного состояния с наполовину уменьшенной электронной заселенностью высшей занятой электронами орбитали.

12. Электронная структура атомов с точки зрения квантовой химии

Однодетерминантная волновая функция многоэлектронного атома, отвечающая определенным проекциям N-электронного орбитального L и спинового S моментов, не обязательно является собственной функцией операторов квадрата полного орбитального L2 и спинового S2 моментов атома. Тогда собственные функции этих операторов являются линейными комбинациями детерминантов Слейтера, отвечающими одним и тем же

N	N
значениям квантовых чисел полных орбитального L = ∑li	и спинового S = ∑ S i моментов в пределах
i	i

некоторой электронной конфигурации. Под электронной конфигурацией атома понимают определенное рас-

пределение электронов по оболочкам:	(nl)k1	,	(nl)k2	, (nl)k3 ...., (nl )kb . Каждая (nl)i оболочка представляет
	1		2	3	b
					b
собой набор 2(2li+1) спин-орбиталей,	из которых kj			спин-орбиталей	(∑k j	= N) заняты электронами и
					j
включены в детерминант Слейтера.	Эти kj		спин-орбитали можно		выбрать	для каждой (nl)i оболочки

Сk2(j2li +1) способами, как это следует из правил комбинаторики. Например, для электронной конфигурации

атома углерода (1s)2 (2s)2 (2p)2 можно построить 15 детерминантов, а из них составить 15 линейных комбинаций, соответствующих определенным значениям квантовых чисел L и S.

Таким образом, каждой электронной конфигурации соответствует некоторое число однодетерминантных функций, определяемое числом незамкнутых оболочек. Совокупность этих функций, характеризующаяся одними и теми же значениями квантовых чисел орбитального L и спинового S моментов, называется термом. Отдельные волновые функции терма отличаются квантовыми числами проекций этих моментов Lz и Sz. Если пренебречь спин-орбитальным взаимодействием, то все волновые функции терма отвечают одному и тому же (2L+1)(2S+1) кратно вырожденному энергетическому уровню атома. Спин-орбитальное взаимодействие расщепляет этот вырожденный уровень на так называемые уровни тонкой структуры. Энергия терма равна средневзвешенному значению энергий уровней тонкой структуры. Именно минимум этой энергии определяет порядок, в котором электроны заполняют атомные оболочки. Отсюда следует, что понятие электронной конфигурации атома не является строгим физическим понятием, а зависит от приближения, в котором рассматривается атомная электронная структура.

В то же время, оболочечная структура атомов является объективным фактом, определяющим в конечном счете периодические свойства элементов. Полная ЭП оболочечную структуру явно не показывает и важно иметь способ надежно выделить электронные оболочки атомов. Рассмотрим этот вопрос более подробно.

Электронная плотность атома является скалярной функцией координаты r. Как известно, имеет ли скалярная функция максимум или минимум в точке экстремума, определяется знаком ее второй производной или кривизной в этой точке. Кривизна одномерной функции f(x) отрицательна в точке x, если значение f(x)

26

больше среднего значения этой функции в соседних точках x+dx и x–dx, и положительна в противоположном случае.

ЭП атома имеет максимум в положении ядра и спадает по мере удаления от ядра. Рассмотрим одномерную функцию f(x), моделирующую распределение электронов в атоме вдоль радиального направления, а

также ее первую и вторую производные (рис. 10). Угол наклона f(x) в точке x1– x больше, чем в точке x1+ x, вторая производная по х в точке x1 отрицательна, а это значит, что кривизна f(x) в точке x1 положительна. На-

клон f(x) в точке x2+ x больше, чем в точке x2– x, т.е. кривизна f(x) здесь отрицательна. В области от x1 до x2 функция f(x) имеет точку перегиба, в которой кривизна равна нулю.

Говорят, что f(x) концентрируется в областях, в которых	d2f (x)		d2f (x)
		<0 и разрежается при		>0.
	dx2		dx2

Понятно, что f(x) максимально концентрируется в точке, где отрицательная кривизна максимальна. Наличие областей локальной концентрации или разрежения f(x) не связано с наличием максимумов или минимумов самой функции. Например, функция f(x), изображенная на рис. 10, имеет максимум при х=0 и других экстрему-

	мов не имеет (т.е. отсутствуют точки, в которых f '(x)=0), а области, где	d2 f (x)	<0 и	d2 f (x)	>0 имеют место.
		dx 2		dx 2

Все сказанное справедливо и в случае трех измерений, в частности, справедливо для функции ρ(r). В этом случае необходимо рассматривать вторые производные по трем координатам – лапласиан ЭП:

	2 ρ(r) =	∂2	ρ	+	∂2	ρ	+	∂2 ρ	(78)
		∂x2			∂y2			∂z2

В направлении от ядра ЭП экспоненциально уменьшается, и в общем случае кривизна ρ(r) вдоль радиального направления от ядра положительна, как и f(x) в точке x1 на рис. 10. Однако две компоненты кривизны,

перпендикулярные радиальной линии, отрицательны. Таким образом, функция 2ρ(r) будет принимать разные знаки по мере удаления от ядра, явно проявляя электронные оболочки атома.

Для каждой квантовой оболочки наблюдается пара областей (одна отрицательная и одна положительная) с внутренней областью, представляющей собой максимум концентрации электронов. Поскольку ЭП кон-

центрируется при 2ρ<0, локальный максимум − 2ρ будет соответствовать максимуму концентрации ЭП, а ло-

кальный минимум − 2ρ указывает на локальное разрежение ЭП.

Распределение лапласиана ЭП в некоторых атомах приведено на рис. 11. Из рисунка видно, что 2ρ − действительно удобная функция для анализа строения электронных оболочек атомов.

27

Рис. 10. График монотонно убывающей функции f(x) и ее первой и второй производной

28

- 2ρ

Рис. 11. Лапласиан ЭП атомов водорода (а), неона (б), лития (в), бериллия (г), бора (д), углерода (е), азота (ж) и кислорода (з). Расчет UHF/6-31G(d))

Важно, что лапласиан ЭП определяет концентрацию электронов на валентной оболочке. Эта квантовая обо-

лочка атома также разделена на внутреннюю область, в которой 2ρ<0 и внешнюю, в которой 2ρ>0. Часть оболочки, внутри которой 2ρ<0, носит название области концентрации заряда валентной оболочки (КЗВО). При образовании химической связи валентная оболочка искажается, приводя к появлению максимумов, соответствующих числу и относительному расположению электронных пар, отвечающих предсказаниям модели Льюиса и модели отталкивания электронных пар валентной оболочки Гиллеспи.

Оболочечная структура атома проявляется в радиальной функции распределения (52) по иному. Максимум функции радиального распределения определяет значение r, в котором с наибольшей вероятностью можно обнаружить ЭП, усредненную по бесконечно малому объему, лежащему между двумя концентрическими сферами радиуса r и r+dr. Однако фактическое распределение ЭП в трехмерном пространстве максимумом в этой области не обладает.

13. Квантово-химическая трактовка решений одноэлектронных уравнений

Хартри-фоковские энергии орбиталей εi имеют вполне определенный физический смысл. Если удалить с орбитали χi один электрон (ионизировать атом), изменение энергии системы можно приближенно записать как

		N		1
	E ≈ −εi = − hi +∑ Jij −				Kij	,	(79)
				2
		j

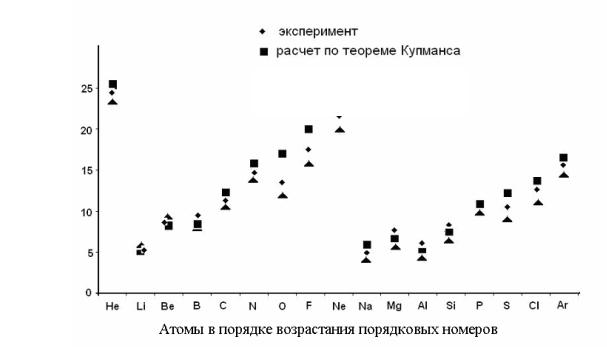
считая, что после удаления электрона система не перестроится (останется “замороженной”). Этот результат называется теоремой Купманса. Мы видим, что орбитальные ХФ-энергии дают оценку потенциалов ионизации I

29

− энергий, которые необходимо сообщить системе, чтобы удалить какой-либо из ее электронов. По потенциалу ионизации можно судить о прочности связи электрона данной орбитали с атомным остовом.

Первый потенциал ионизации I1 описывает энергию отрыва электрона с высшей занятой атомной орбитали. При этом предполагается, что и исходный атом, и образовавшийся ион находятся в основных (невозбужденных) состояниях. Потенциалы ионизации I2, I3, I4 и т.д. отвечают дальнейшим последовательным отрывам электронов от ионов. Для атома с N электронами I1 < I2 < I3 <I4 …< IN. Например, для атома углерода первые потенциалы ионизации с верхней занятой 2p-АО и глубинной 2s-АО составляют соответственно 11.26 и 20.0 эВ. Зависимость потенциала ионизации от порядкового номера элемента имеет ярко выраженный периодический характер, что иллюстрирует рис. 12.

I1, эВ

I1 = E(N) – E(N–1)

Рис. 12. Зависимость потенциалов ионизации элементов от атомного номера

В пределах периода, как правило, с увеличением атомного номера потенциалы ионизации возрастают. Исключения связаны с устойчивостью замкнутых оболочек (IО < IN; IMg > IAl) с максимальной мультиплетностью. Для экспериментального определения I применяют фотоэлектронную и рентгеноэлектронную спектроскопию.

Более точно потенциал ионизации следует вычислять с помощью выражения (76). Тогда первый потен-

циал ионизации, вычисляется как разность ХФ энергий атома и образующегося иона:
I1 = E(N) – E(N–1)	(80)

Сродством к электрону Ax называют энергию, которая высвобождается при присоединении к нейтральному атому одного электрона. Наибольшими значениями Ax обладают атомы галогенов. По аналогии со сказанным выше,

A1 = E(N+1) – E(N),

(81)

т.е. сродство к электрону можно приближенно охарактеризовать энергией низшей свободной (виртуальной) АО.

30

Приравнивая нулю дифференциал функционала электронной энергии (73) при постоянном числе электронов и при неизменном ядерном потенциале

d{E[r] - μN[r(r)]}Vяд =const = 0,			(82)
(N = ∫ ρ(r) dv), можно определить электронный химический потенциал μ:
	∂E
μ =			(83)
	∂N Vяд =const

При образовании химической системы из атомов химический потенциал выравнивается, при этом проис-

ходит переток электронов к атому с большим значением μ. По смыслу это совпадает с эмпирически введенной Полингом электроотрицательностью.

На рис. 13 представлена зависимость энергии атома от числа электронов. Как видно из рисунка, μ харак-

∂E

теризует наклон кривой E = E(N). Представим производную ∂N в конечно-разностном виде (предполагая Е

гладкой функцией N):

μ ≈	E(N +1)	− E(N −1)	=		[E(N +1) − E(N )] +[E(N ) − E(N −1)]		(84)
	(N +1)	−(N −1)
						2
Отсюда следует
		μ ≈ −		I + A		,	(85)
			2

что с точностью до знака совпадает с определением электроотрицательности по Малликену (I1 – первый потенциал ионизации, А – сродство к электрону).

Рис. 13. Зависимость энергии атома от числа электронов

Определенная таким образом величина

	χ =	I + A	(86)
		2

называется абсолютной электроотрицательностью (Парр и др., 1978).

Пирсон (1983), действуя аналогичным образом, показал, что скорость изменения химического потенциа-

ла μ при изменении числа электронов N есть абсолютная химическая жесткость