1.4. Построение поверхности

Обеспечивается следующим текстом программы (см. рис. 1.6)

% подготовка к построению графика

masx=xleft:hx:xright;

masy=yleft:hy:yright;

masz=fz_xy2(masx,masy); построены массивы координат для точек

%графика

mesh(masx,masy,masz); %построена сеточная поверхность

grid on;

title(‘z=-sqrt(256-x.^2-y.^2)’);

xlabel(‘X’);

ylabel(‘Y’);

zlabel(‘Z’);

text(x,y,z,’\leftarrow Minimum’);

legend(‘z(i,j)=-sqrt(256-x(i)*x(i)-y(j)*y(j))’,0);

где команда mesh(masx,masy,masz); строит сеточную поверхность .

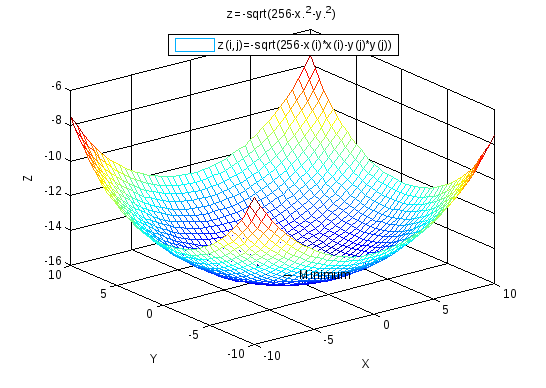
Рис. 1.6. Пример построения поверхности

1.5. Операции с матрицами.

Пусть даны две матрицы. (Если не даны, зададим их. Пусть

A=[1 2 3; 5 67 89; 34 21 5];

B=[3 4 5; 54 32 12; 6 7 8];

Тогда имеем две матрицы 3х3 элемента).

Транспонировать матрицу можно так

A_transp=A’; где знак ’ обеспечивает транспонирование матрицы А.

Умножение матриц выполняется так

C_res_mult=A*B; где C_res_mult результат умножения матриц.

Обратная матрица находится так

А_obr=A^(-1);

Или так: A_obr=inv(A);

Поэлементное сложение матриц C=A+B;

Определитель D=det(A);

Решение системы линейных уравнений, где А матрица системы, столбец b столбец свободных членов, столбец х столбец неизвестных:

x=linsolve(A,b);

1.6. Нелинейные уравнения и системы

Решить алгебраическое уравнение вида a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n=0 можно функцией x=roots(p); где x вектор корней алгебраического уравнения (полинома), p вектор коэффициентов полинома, то есть р=[a₀ a₁ …a_n-1 a_n]. Например, для уравнения х²-1=0 вектор р=1 0 -1 тогда х=roots(p) и получается, что х=1 -1. Это и есть корни уравнения.

Уравнение, в котором неизвестное входит в аргумент трансцендентных функций, называется трансцендентным уравнением. Для решения их, предварительно приведенных к виду f(x)=0, используют функцию fzero.

Формат ее вызова таков: [x,y]=fzero(name,x0); где

name имя М-функции, вычисляющей левую часть уравнения вида f(x)=0.

x0 начальное приближение или интервал его изоляции [a, b];

Например пусть f(x)= 0.2e^x -2(х-1)² тогда см. рис.1.7

На рис.1.7 показано, что при трех разных интервалах изоляции корня найдены три различных корня, которые были помещены в массив х по одному, по мере их нахождения, как х(1), х(2) и х(3), а затем выведены в строчку все три как содержимое массива х.

Аналогично поступили со значениями функции у(1), у(2) и у(3). Их нахождение было важно для контроля того, что действительно значения функции очень близки к нулю (они все получились порядка 10^-15, что практически и есть ноль, с учетом вычислительных погрешностей).

Рис. 1.7. решение уравнения при различных интервалах изоляции корня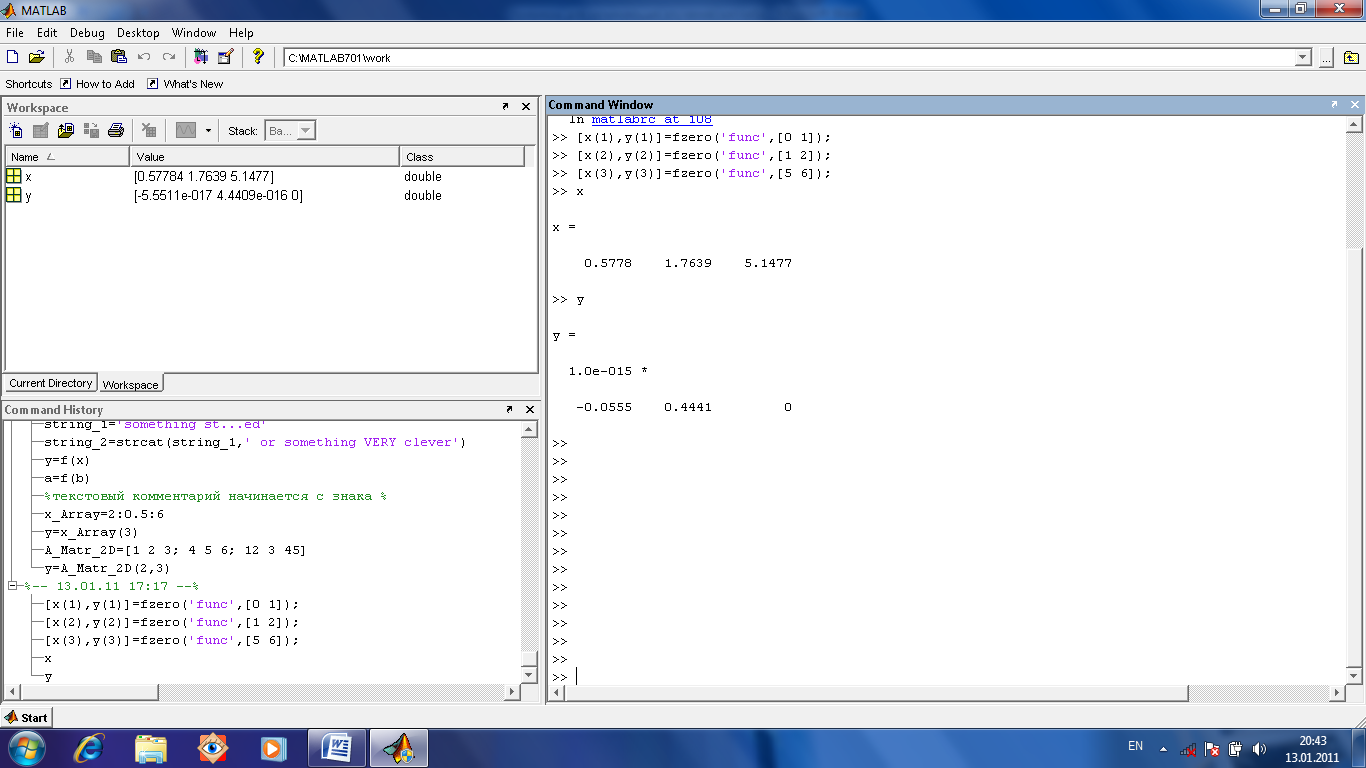

Слева на рис.1.7 видно окно Workspace, где отображены значения переменных и их тип. В принципе, в данной задаче эта информация дублируется в обоих окнах (то есть в Command Window и в Workspace).

Содержимое функции func продемонстрировано на рис.1.8.

рис. 1.8. функция func(x)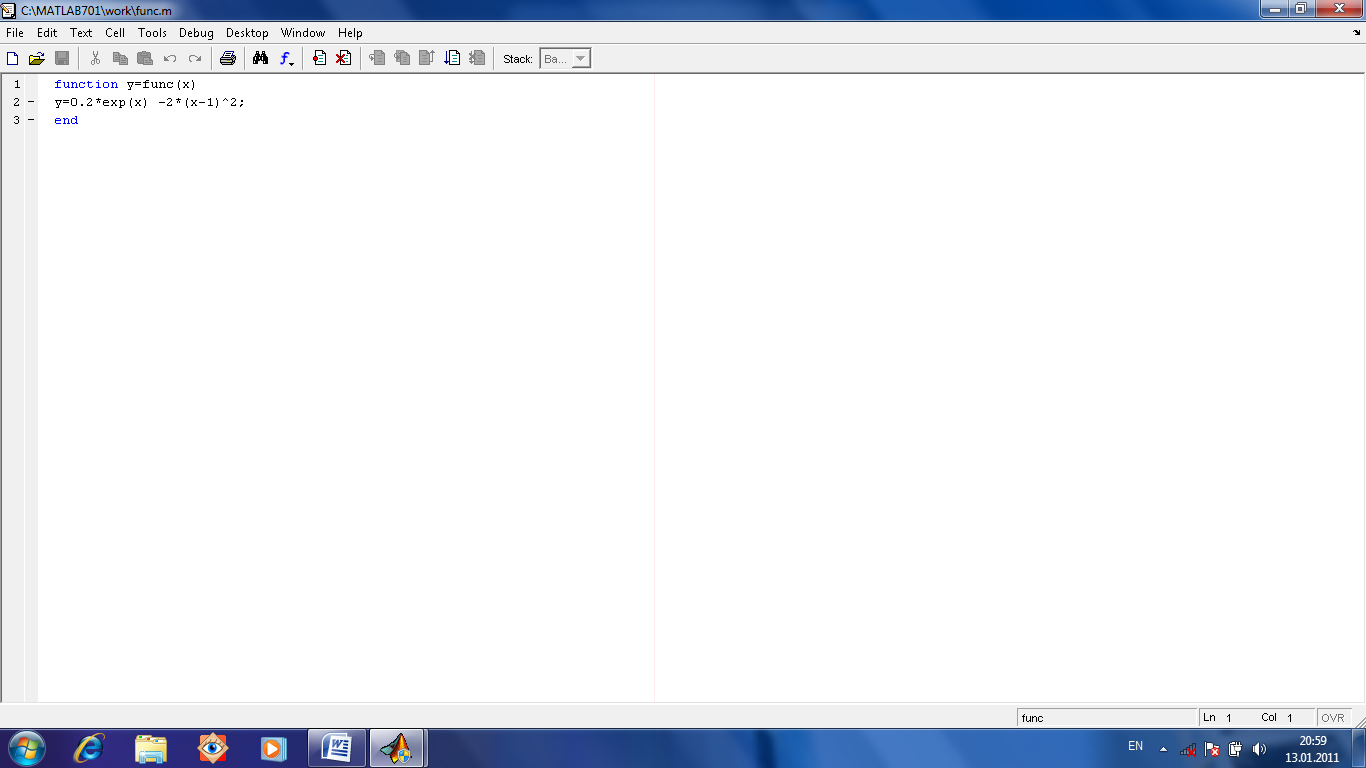

1.7. Интегрирование

Для решения определенного интеграла методом трапеций предусмотрена функция trapz.

Пример для вышеописанной функции func (см. рис.1.8), (где для обработки вектора аргументов поставлена точка перед знаком возведения в степень y=0.2*exp(x) -2*(x-1).^2; ) при пределах интегрирования [0 1] с шагом разбиения 0,1 приведен на рис.1.9.

Вполне очевидно, что с ростом числа точек разбиения по х (числа шагов, то есть при уменьшении шага по х) будет расти точность вычисления интеграла.

На рис.1.9 наглядно показано разбиение интервала интегрирования по х с заданным шагом, а также вектор значений функции в точках разбиения по х (то есть при данных значениях аргумента).

Получилось значение интеграла равное -0,3261.

Рис. 1.9. Интегрирование