1.8. Решение обыкновенных дифференциальных уравнений и систем.

Дифференциальным уравнением n-го порядка называется уравнение:

H(t, x, x^’, x^’’, … , x⁽ⁿ⁾)=0

Решением дифференциального уравнения называется функция x(t), которая обращает уравнение в тождество.

Системой дифференциальных уравнений n-го порядка называется система вида:

x₁^’=f₁(t, x₁, x₂, x₃, … , x_n)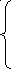

x₂^’=f₁(t, x₁, x₂, x₃, … , x_n)

…………………………..

x_n^’=f₁(t, x₁, x₂, x₃, … , x_n)

Системой линейных дифференциальных уравнений называют систему вида:

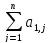x₁^’=x_j + b₁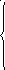

x₂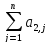^’=x_j + b₁

.…………………..

x_n^’=x_j + b₁

Решением системы является вектор x(t)=x₁(t), x₂(t), … ,x_n(t), который обращает вышеприведенные системы уравнений в тождества.

Различают:

Задачу Коши, когда все дополнительные условия заданы в одной (чаще всего в начальной) точке интервала значений t.

Краевую задачу, когда дополнительные условия заданы на границах интервала значений t.

Есть много встроенных функций, обеспечивающих решение вышеуказанных задач.

Ниже описаны некоторые из них с примерами их использования.

Входными параметрами этих функций являются:

• f вектор-функция для вычисления правой части уравнения вида x^’=f(x,t), удовлетворяющей начальному условию x(t₀)=x₀ или системы дифференциальных уравнений, данных в матричном виде dx/dt=f(t,x) с начальным условием x(t₀)=x₀ данным в матричном виде.

• interval массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы.

• X0 вектор начальных условий системы дифференциальных уравнений.

• options параметры управления ходом решения дифференциального уравнения или системы уравнений.

Все функции возвращают:

• Массив Т содержащий координаты узлов сетки, в которых ищется решение.

• Матрицу Х в которой i-й столбец является значением вектор-функции решения в узле T_i.

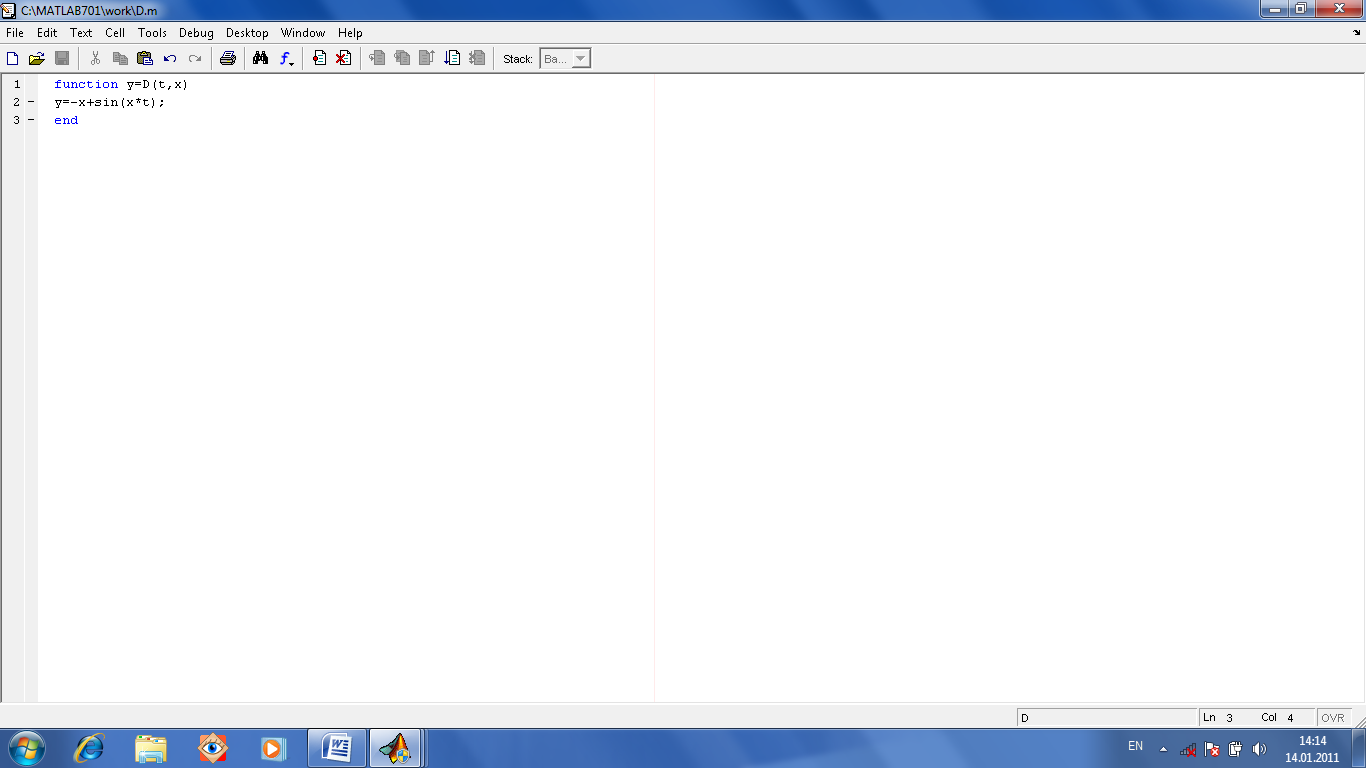
Решим задачу Коши: Рис. 1.10. функция D(t,x)

dx/dt + x =sin xt при x(0)=1.5. Напишем М-функцию (рис. 1.10)

Используем функцию ode113, которая реализует метод Адамса. В качестве ее параметров используются: @D ссылка на М-функцию, [0 35] интервал интегрирования уравнения, начальное условие x(0)=1.5 указано в виде 1,5 на соответствующем месте в списке параметров.

Обращение к функции: ode113(@D, [0 35], 1.5). Она строит график решения (см.рис.1.11).

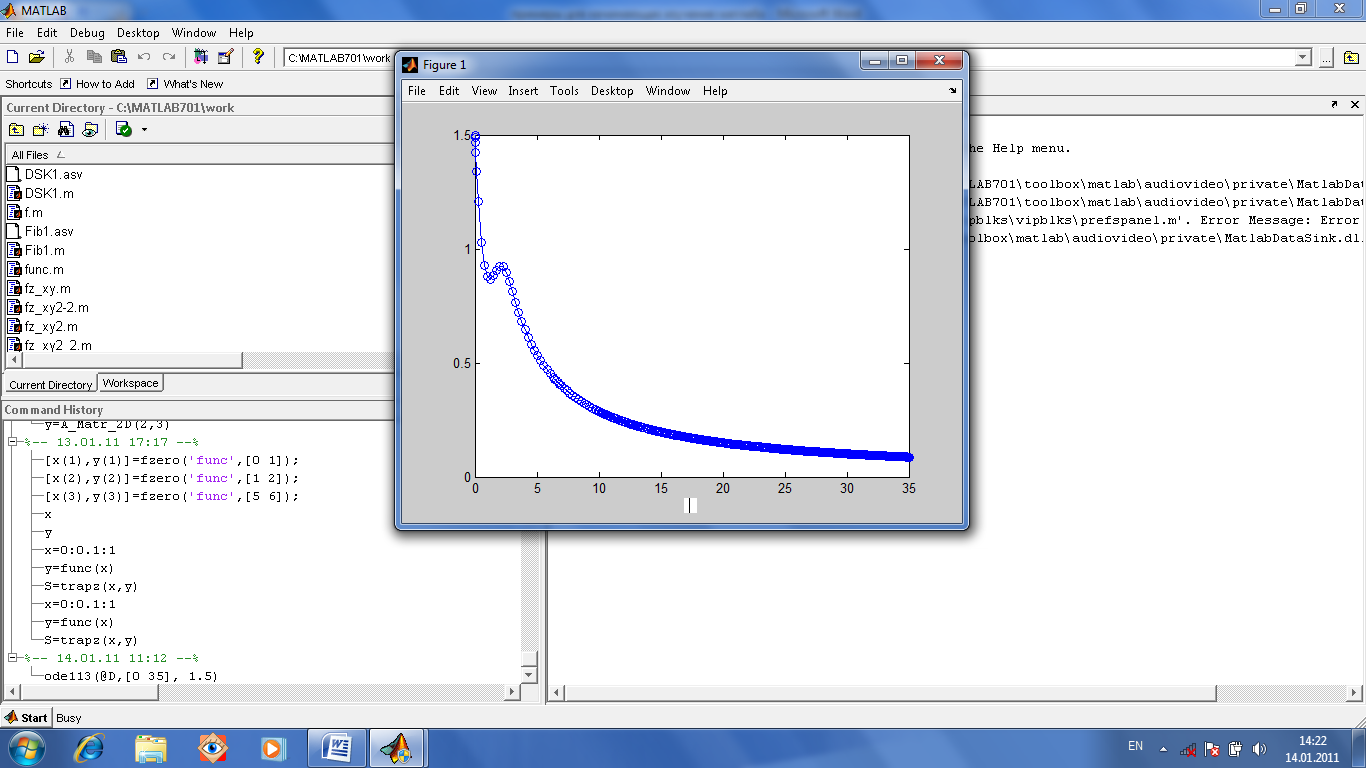
Рис. 1.11. функция ode113 строит график решения

Напишем М-функцию syst (см. рис.1.12)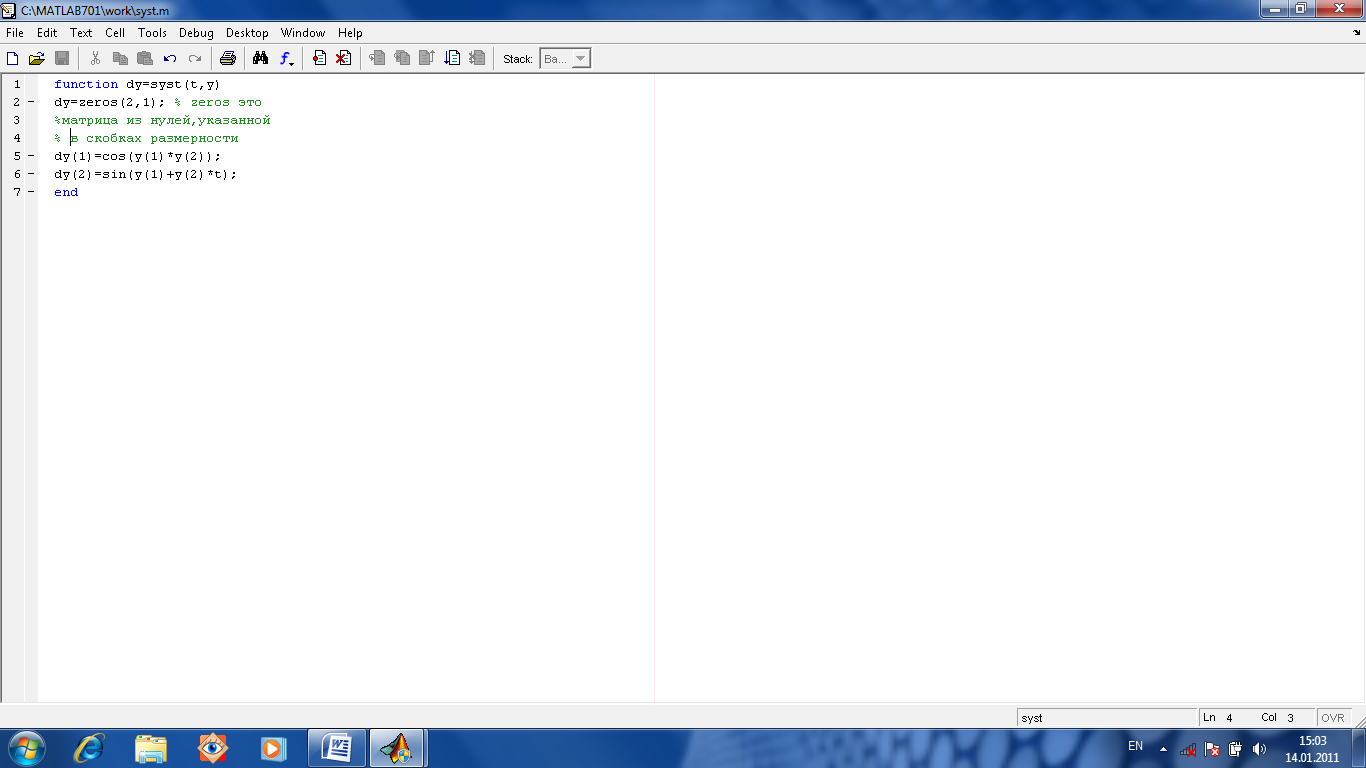

Используем функцию ode23 решающую методом Рунге-Кутта 2-3 порядка. Ее вызов

[T, Y]=ode23(@syst, [0 10], [0 0]); Рис. 1.12. функция syst(t,y)

где явно указаны выходные параметры вектор Т и матрица Y, а также указаны интервал [0 10] и начальные значения [0 0].

Затем формируем график решения plot(T,Y,’k-‘). Получаем график (см.рис.1.13)

Рис. 1.13. график решения

1.9. Поиск экстремума функции одной переменной.

При решении задач поиска максимума (минимума) выделяют локальный (с указанием границ) и глобальный максимум (минимум). Локальный минимум функции одной переменной ищет встроенная функция [x, y]=fminbnd(name, a, b, options). В ней:

• name имя М-функции,

• a, b границы поиска,

• options параметры управляющие ходом решения,

• x, y координаты точки минимума.

Для вычисления локального максимума, надо взять функцию name с другим знаком. Для примера, рассмотрим функцию y(x)=x⁴-0.5x³-28x²+140

Сначала найдем минимум на интервале, например, от -4 до -2.

[x,y]=fminbnd(@ext,-4,-2), где @ext обращение к М-функции вычисляющей интересующую нас функцию.

Потом найдем максимум на интервале от -6 до 6, для этого обратимся не к @ext, а к @ext_2, в которой функция y(x) взята с другим знаком, то есть y(x)=-(x⁴-0.5x³-28x²+140). То есть ее минимум будет максимумом исходной функции.

Получим и в том, и в другом случае координаты точки минимума (максимума) на заданном отрезке, что и требовалось.