ИГ / КЛАССИФИКАЦИЯ кривых поверхностейt

120	Р а з д е л 1. Ортогональные проекции
					i	γπ		Z3 i
A2						2
	B2	απ2			2			3
M2	n2	M3 n3	C	K		D	2	K
				2	2			3
	l2	m3						a2
m2	N2	N3
		l3
M1	n1
	l1 B1	X1	C1		i	D1		σπ1
m1					1	a
						1		τπ1
A1					M1
					K1 F1			δπ1
		1
(N1)		βπ
	а				E1
						б
			Рис. 154

ционной связи: расстояние от горизонтальной проекции точки до оси Х1 равно расстоянию от профильной проекции точки до оси

Z3 ≡ i3.

8.7. Плоские сечения геометрических тел

При построении контура сечения геометрического тела плос! костью решаются основные позиционные задачи на определение точки встречи прямой (образующей или ребра) с плоскостью се! чения и линии пересечения двух плоскостей (грани и секущей плоскости). Поэтому фигуру сечения можно рассматривать как множество точек пересечения ребер или образующих с плоско! стью (рис. 155). На пирамиде и призме получаются многоуголь! ники, на конусе и цилиндре — прямые и кривые 2!го порядка, на шаре — окружности, на торе — окружности, кривые Персея (ова! лы Кассини, лемнискаты Бернулли и Бутта) и другие замкнутые кривые. Надо знать условия, при которых получается тот или дру! гой вид сечения.

Рассмотрим образование кривых на конусе. Если секущая плоскость пересекает все образующие конуса, получится замкну! тая кривая — эллипс (рис. 156, а). Секущая плоскость α задана

Т е м а 8. Образование поверхностей, их классификация... 121

Рис. 155

следом απ1 и точкой А на образующей конуса. Выделяем на кону! се образующую SB1, через нее проводим вспомогательную плос! кость σ, находим линию пересечения плоскостей α и σ — линию АМ. Точка В = SB1 × АМ. Аналогично находятся другие точки, со! единив которые, получаем эллипс — фигуру сечения. Если секу! щая плоскость β параллельна образующей SA (рис. 156, б), то в се! чении получим параболу. Признаком параллельности прямой и плоскости является наличие прямой ВС || SA в плоскости β (пря! мая параллельна плоскости, если она параллельна какой!нибудь прямой этой плоскости).

Плоскость β пересекает одну полость конуса общего вида (рис. 157, а). Плоскость γ параллельна двум образующим конуса SA и SB (рис. 156, в и рис. 157, а). В этом случае плоскость γ пере! сечет обе плоскости конуса (рис. 157, а). Кривая будет состоять из двух ветвей — это гипербола.

122	Р а з д е л 1. Ортогональные проекции
	S
	S	A
	B	B
	A
	B1	S

σπ1	A1	B	C
			A	γπ1
			б
	B1	απ1
				γπ1
		M		в
		а
			Рис. 156

			τ	τ
		α
γ	S		σ	σ
	β
			б
	а			в
			Рис. 157

На цилиндре может получиться только эллипс или окружность, если секущая плоскость σ пересекает все образующие цилиндра. Если секущие плоскость τ параллельна оси цилиндра, то получит! ся четырехугольник (рис. 157, б).

Пример 1. Построить сечение призмы плоскостью α (απ1) и в натуральную величину фигуру сечения плоскопараллельным пе! ремещением (рис. 158).

Решение задачи начинается с анализа условия задачи. На рис. 158 дано изображение наклонной трехгранной призмы. Секущая

Т е м а 8. Образование поверхностей, их классификация...																	123
						A2′	B2′	C2′
																НВ
				42								42′				32′
									απ2
	A2			B2			32
X12						C2				12′			22′
			12		22	C1
								C1′
	A			4			31		απ1′	1		′ 4 ′	2		′	3 ′
		1			1						1			1
						21						1				1
1			11			A1′
απ
				B1			B1′
								Рис. 158

плоскость α π1, горизонтальный след απ1 обладает собиратель! ным свойством. Значит, горизонтальная проекция фигуры сече! ния уже известна. Отмечаем точки 11 и 21 пересечения плоскости α со сторонами основания призмы. В грани В1С1С′1В′1след απ1 пе! ресекает ребро С1С′1 в точке 41 и затем в точке 31 — ребро А1А′1. Находим фронтальные проекции точек 1–4, соединяем их с уче! том видимости (грань АСС′А′ — невидимая).

Натуральную величину определим способом плоскопараллель! ного перемещения. След απ1 повернем и переместим за пределы горизонтальной проекции призмы и расположим параллельно оси Х12, т. е. параллельно фронтальной плоскости проекций. При этом уровни точек относительно горизонтальной плоскости про! екций не меняются. Из точек 42, 32 проводим горизонтальные прямые до пересечения с проецирующими лучами, проведенны! ми из новых горизонтальных проекций 1′1, 2′1, 4′1, 3′1. Точки 1′2 и 2′2 будут лежать на оси Х12.

Пример 2. Построить сечение пирамиды плоскостью β (D, E, F) (рис. 159).

Анализируем условие задачи: пирамида трехгранная наклон! ная, плоскость β общего положения. Надо строить обе проекции фигуры сечения.

1 й вариант решения: можно трижды решать основную позици! онную задачу на нахождение точек встречи ребер пирамиды с се!

124

Р а з д е л 1. Ортогональные проекции

S2

E2

12

62

≡72

42

L2

K2

32

h2

D2

52

22

F2

X12

π2

A2

B2

M2

π1

B1

E

1

6

1

C2

1

h

31

11

C1

F1

B3

A1

41 ≡51

K1

21

M1

A3

D1

L1

71

S1

E3

K3

M3

βπ1

σπ1

βπ3 h ≡D

L3

F3

3

3

π3

π1

X13

S3

Рис. 159

кущей плоскостью. Через ребро SB проведем горизонтально про! ецирующую плоскость σ. След σπ1 ≡ S1B1. Найдем линию пересе!

чения двух плоскостей 1–2 = β × σ. Горизонтальная проекция 11–21 ≡ σπ1, точка 12 D2Е2, 22 D2F2, К2 = S2B2 × 12–22. Аналогич!

но находят точки пересечения ребер SA и SC с плоскостью β. Но

Т е м а 8. Образование поверхностей, их классификация... 125

можно произвести замену плоскости π2 на π3 с тем, чтобы плос! кость β преобразовать в проецирующую и упростить нахождение проекций фигуры сечения.

2 й вариант решения: новая плоскость π3 должна быть перпен! дикулярной к горизонтали плоскости β. Тогда плоскость β будет перпендикулярна к новой плоскости проекций π3 (если плоскость

проходит через перпендикуляр к данной плоскости, то и плоскость будет перпендикулярна к той же плоскости). Строим в плоскости β горизонталь D–3 (D232 и D131). Новая ось Х13 D131. Строим но! вую проекцию плоскости β (βπ3) и новую проекцию пирамиды: точки А, В, С лежат на горизонтальной плоскости. Их новые про!

екции А3, В3, С3 лежат на оси Х13, координаты Z точек S3, D3, E3, F3 и S2, D2, E2, F2 одинаковы. Точки E3, D3, F3 лежат на одной пря!

мой, следе βπ3, обладающем собирательным свойством, следова! тельно, точки пересечения ребер с плоскостью β сразу определят! ся. К SB, L SA, M SC. Обратным проецированием определяются сначала горизонтальные проекции К1, L1, М1, затем фронтальные К2, L2, М2. Чтобы определить видимость ребер пира! миды относительно плоскости β, надо использовать конкурирую! щие точки. Рассматриваем две скрещивающиеся прямые SA и DE. На виде сверху они пересекаются в точке 41 ≡ 51. Смотрим сверху (по направлению оси ОZ). Точка 42 стороны D2E2 ближе к наблю! дателю, т. е. плоскость β перекрывает ребро SA до точки L1. На виде спереди рассмотрим точки 62 ≡ 72 (E2F2 × S2A2). Смотрим на них спереди (по направлению оси OY). Точка 71 ближе к наблюда! телю, значит, S2L2 — видимая часть ребра S2A2.

Пример 3. Построить сечение прямого кругового конуса плос! костью α (απ1) (рис. 160).

Анализируем условие задачи: конус прямой круговой, стоящий основанием на горизонтальной плоскости проекций. Плоскость α π1, || SO, т. е. параллельна двум образующим, лежащим в плос! кости β || α, и проходящей через вершину S (SC и SD). В сечении конуса плоскостью α получится ветвь гиперболы. Точки А и В на основании уже известны. Чтобы определить горизонтальную про! екцию вершины гиперболы С1, опустим из точки S1 απ1, радиу! сом S1C1 проведем окружность, которая с горизонтальным диа! метром основания пересечется в точке 11, ее фронтальная проекция лежит на очерковой образующей S2E2. Через точку 12

126	Р а з д е л 1. Ортогональные проекции
			S2
		C2		12		τπ2
	σπ2	42	52		22
			O2′
	σπ2′	62		72		32
			O2′
	X12
	A2		O2		B2	E2
		O1	≡S1 1		21 31 E		1
			1
	A1	41						βπ
		61	51			D1
		C1						1
			71				απ
					B1
								1
		Рис. 160

проходит след горизонтальной плоскости τπ2, в которой лежит окружность радиуса S1С1. Фронтальная проекция вершины С2 ле! жит на следе τπ2.

Для построения промежуточных точек 4 и 5, 6 и 7 фигуры сече! ния используем горизонтальные вспомогательные секущие плос! кости σ и σ′. В сечении конуса получаются окружности радиуса О2′22 и О2′′32, которые на виде сверху пересекаются с собиратель! ным следом απ1 в точках 41 и 51, 61 и 71. На пересечении проеци! рующих лучей и следов σπ2 и σ′π2 получаются фронтальные про! екции точек 42 и 52, 62 и 72. Полученные фронтальные проекции точек А2 62 42 С2 52 72 В2 соединяем лекальной кривой. Вся кривая — видимая линия, так как все точки лежат на передней видимой ча! сти конуса (перед горизонтальным диаметром основания — гра! ницей видимости).

Т е м а 8. Образование поверхностей, их классификация...																							127
Пример 4. Построить сечение конуса плоскостью α (m ′ n) и на!
туральную величину фигуры сечения (рис. 161).
								S2
		N2		απ2 ≡n2
				f
				2			32
						42
			σπ	2			a ≡h			62					K2		βπ2
						52	2		2
			σπ2′				72					82					K2′
														42′
X	12		A			n1 ≡m2				12		D	2				O		α		x
			2														2
	N					C2				M2			22 B2			K1′
		1										32′							O1		K0′
		γπ1
					C1 31																	βπ1
										61
	τπ1 ≡f1					41		S1			81						h	0
												41′			B1
																						K0
			A1																	′
															21		80		h		0
							5			M1			D						6
								71							1					0
							1
					h	1				11
							m	1
								απ1			70
																					30	(απ2)0
														50			40
										Рис. 161

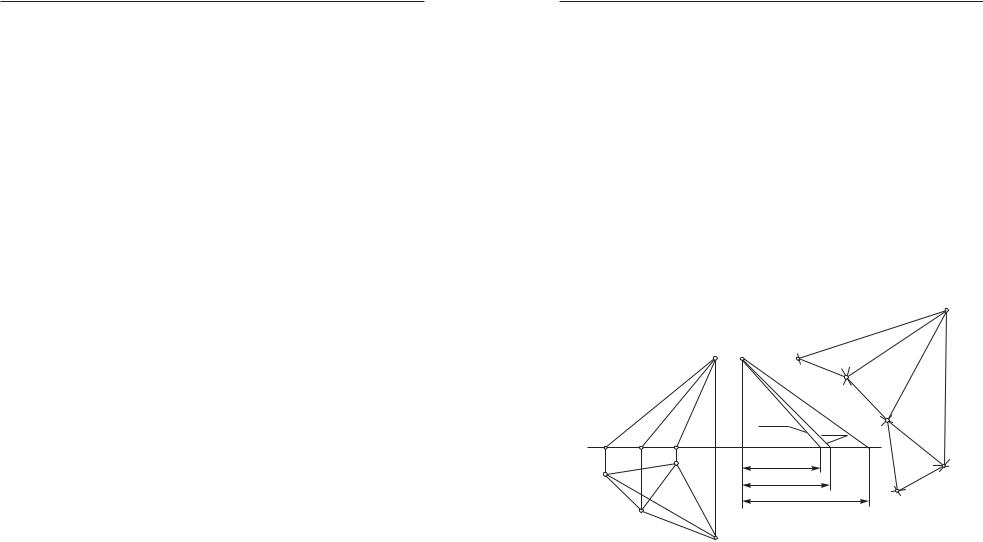
Дан конус прямой круговой, плоскость α, заданная горизонта! лью и фронталью нулевого уровня, являющимися следами плос!

кости α (n2 ≡ απ2, m1 ≡ απ1). Ни один из следов не Х12, значит, плоскость α общего положения, наклонена к оси конуса SO, в се!

чении получится эллипс, который не вырождается в прямую ли! нию. Значит, надо строить обе проекции эллипса (неполного, так

128 Р а з д е л 1. Ортогональные проекции

как след απ1 пересекает основание конуса в точках 1, 2). Рассмот! рим решение этого примера.

1.При построении проекций наклонного эллипса сначала оп! ределяют наивысшую и низшую точки эллипса (опорные точки),

которые находятся на линии наибольшего ската, перпендикуляр! ной к горизонталям плоскости или следу απ1. M1N1 απ1, M2N2 — фронтальная проекция линии ската определяется по точкам. Линия

ската проводится через горизонтальную проекцию вершины S1. Чтобы найти точки пересечения линии наибольшего ската с ко!

нусом, проведем через нее горизонтально проецирующую плос! кость γ. Она пересечет конус по образующим SC и SD, которые

лежат в одной плоскости с линией ската и, пересекаясь с нею, оп! ределяют точки 3 и 3′, выше и ниже которых не будут лежать точ! ки эллипса (точка 3′ лежит ниже основания и не участвует в пост! роении проекций эллипса). Линия наибольшего ската не параллельна образующим конуса. Это доказывает, что в сечении получится эллипс.

2.Следующие опорные точки должны принадлежать очерко! вым образующим и являться границами видимости фигуры сече!

ния на виде спереди. Проводим вспомогательную фронтальную

плоскость τ (τπ1 || Х12). Конус пересечется по очерковым образующим SA и SB, а плоскость α — по фронтали f(f1 ≡ τπ1, f2 || απ2). В пересече!

×S2А2 и f2 × S2В2 получаем точки 4 и 4′(42 и 42′ и 41 и 41′).нии f2

3. Промежуточные точки 5–8 находят при помощи вспомога! тельных горизонтальных плоскостей, проведенных произвольно

ниже точки 3. Плоскость σ пересечет конус по окружности а, плоскость α′σ — по горизонтали h (h2 ≡ σπ2, h1 || απ1), проходящей

через точку К2 на следе απ2.

4. Натуральную величину фигуры сечения определим спосо! бом совмещения плоскости α, в которой лежит эллипс, с плоско! стью π1. Вспоминаем, что это есть вращение вокруг горизонтали нулевого уровня или вокруг следа απ1. Способ вращения требует

определения четырех элементов вращения: 1) ось вращения — απ1; 2) плоскость вращения точки К′ απ2 (βπ1 К′1, βπ1 απ1);

3) центр вращения точки К′(О1); 4) радиус вращения точки К′. На! туральную величину радиуса вращения можно не находить, а про! вести дугу радиусом αхК′2 из точки αх до пересечения с плоско! стью вращения βπ1 в точке К′0. Совмещенный фронтальный след (απ2)0 пройдет через точки αх и К′0. Каждая точка эллипса лежит

Т е м а 8. Образование поверхностей, их классификация... 129

на своей горизонтали, которая при совмещении располагается параллельно следу απ1. И в то же время точки лежат в плоскостях вращения β′ απ1.

8.8. Развертки

Разверткой поверхности называется плоская фигура, образован ная последовательным совмещением всех плоских элементов этой поверхности с одной плоскостью (без складок и разрывов). Значит, на развертке откладываются натуральные величины ребер, образу! ющих и фигуры оснований. Развертки используются для построе! ния макетов, разнообразных изделий и конструкций, упаковок.

Общий способ построения разверток сводится к разбивке гра! ней на треугольники, а в конус и цилиндр вписываются много! гранные пирамиды и призмы, для которых и строятся развертки. У пирамиды боковые грани есть треугольники (рис. 162).

S

		S2	A
			НВ	B
				SA
			НВ SB	НВ SC	C
X12	B2	C2
	A2	C1	S1B1
A1					A
			S1C1
			S1A1		B
	B1
		S1	Рис. 162

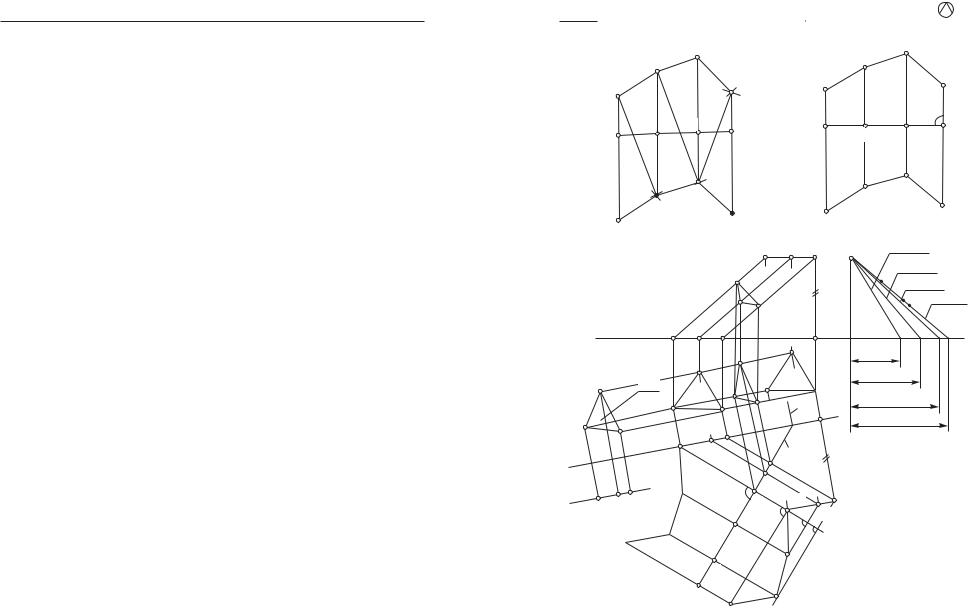
Надо знать натуральную величину каждого ребра. В данном примере стороны оснований изображены без искажения, так как лежат на горизонтальной плоскости проекций. Натуральную ве! личину боковых ребер можно определить способом плоскопарал!

130 Р а з д е л 1. Ортогональные проекции

лельного перемещения. Затем строятся треугольники SCB, SBA, SAC по трем сторонам и треугольник основания АВС.

Теперь рассмотрим способы построения разверток для призмы (аналогично для цилиндра). На рис. 163, а изображена наклонная трехгранная призма. Способом прямоугольного треугольника оп! ределим натуральную величину бокового ребра призмы. Прямо! угольный треугольник выносим в сторону. Одним катетом являет! ся горизонтальная проекция ребра А1А1′ (откладываем на оси Х12), а другим — разность удаления концов отрезка от горизонтальной плоскости проекций ZA′–ZA. Здесь же определяется длина диаго! налей, которые делят каждую грань на два треугольника. Для по! строения развертки проводим произвольную прямую, на ней от! мечаем точку А′ и от нее откладываем натуральную величину АА′ (гипотенузу прямоугольного треугольника). Из точки А′ прово! дим дугу, равную натуральной величине А′С (диагональ грани АА′С′С), а из точки А — дугу, равную натуральной величине АС. Затем достраивается параллелограмм. Так же строятся СС′В,

ВВ′А′ и грани С′В′ВС, В′А′АВ. Если достроить треугольники ос! нований и перенести развертку призмы на плотную бумагу, оста! вить бумагу для склеивания, вырезать, перегнуть по ребрам и склеить модель, то можно увидеть, как были получены проекции призмы, соответствует ли образ наклонной призмы заданному ус! ловию.

На рис. 163, б, в построены развертки призмы еще двумя спо! собами. Введем новую плоскость проекций π3 π1 такую, которая бы расположилась параллельно горизонтальной проекции боко! вого ребра. Х13 || В1В1′. Строим новую проекцию призмы на плос! кости π3. Расстояния до неизменной плоскости π1 не меняются. Проецирование прямоугольное. В′1В′3 Х13, В′2Вх12 = В′3Вх13. Введем произвольную плоскость α, ребрам призмы. Следы плоскости απ3

иαπ1 к проекциям ребра ВВ′ (следы плоскости — это горизонталь

ифронталь нулевого уровня, а прямой угол проецируется как пря!

мой, если одна сторона угла параллельна плоскости проекций). След απ3 обладает собирательным свойством. Фигура сечения оп!

ределяется точками 132333 пересечения ребер призмы со следом απ3. Соответственно определяем горизонтальные проекции точек 112131. Построены проекции нормального сечения. Для построе!

ния развертки надо знать натуральную величину фигуры сечения. Выполним плоскопараллельное перемещение следа απ3 в положе!

Т е м а 8. Образование поверхностей, их классификация...

131

B′

C′

B′

C′

A′

A′

A′

A′

1

2

3

1

НВ

1

2

3

1

B

C

B

C

A

A

A

б

A

а

НВ A′B

A2′

C2′

B2′

12

НВ A′C

1

НВ C′B

22

32

2 3

НВ AA′

X12

π2

BX12

π1

A2

C2

B2

21

C1′

A1′B1

C1

A1′C1

21′

НВ

11

A1′

B1′

C1′B1

A1

απ4

B1

31

11′

A1A1′

BX13

31′

B3

C3

απ3

X13

π1

A3

π3

32

′

23

απ3

13′ 23′

3

′

1

A3′

B3′

3

3

C3′

2

C′

3

1

B′

A′

в

Рис. 163

132 Р а з д е л 1. Ортогональные проекции

ние απ3′ || Х13. Уровни точек 112131 относительно оси Х13 не меня! ются после поворота. На пересечении с проецирующими лучами получаем новые горизонтальные проекции точек 11′21′31′. Теперь известны натуральные величины расстояний между боковыми ребрами. Строим развертку на рис. 163, б способом нормального сечения. Проводим произвольно горизонтальную прямую. На ней откладываем стороны 11′21′31′, т. е., 1–2, 2–3, 3–1, призму также «разрезаем» по ребру АА′, точка 1 лежит на этом ребре. Перпенди! кулярно к этой линии проводим боковые ребра. Вверх откладыва! ем отрезки 1А′, 2С′, 3В ′ и 1А′, взятые на плоскости π3 от следа απ3 до верхнего основания. Достраиваем нижнюю часть развертки. Развертка построена способом нормального сечения.

Теперь рассмотрим построение развертки на рис. 163, в спосо! бом раскатки. На плоскости π3, где определена натуральная вели! чина боковых ребер, рядом строим развертку способом раскатки. Каждая точка верхнего и нижнего основания при «перекатыва! нии» призмы с одной грани на другую перемещается по окружно! сти, которая изображается прямой, перпендикулярной к ребру. Натуральная величина радиуса есть расстояние от одной точки основания до другой. Из точки А′3 проводим дугу А′1С′1 до пересе! чения с перпендикуляром из С′3 к А3А′3. Последовательно из точки С′ проводим дугу радиусом С′1В′1 до пересечения с перпендикуля! ром из точки В′3. Новая развертка построена способом раскатки. Делаем вывод: способом нормального сечения можно строить раз

вертку, если имеется проецирующая секущая плоскость, перпендику лярная к боковым ребрам; способом раскатки развертку можно по строить на той плоскости проекций, на которой построена натуральная величина боковых ребер. Рассмотренные способы по! строения разверток можно использовать для построения развер! ток наклонных цилиндров. Разверткой прямого кругового цилин! дра является прямоугольник, длина его равна длине окружности С = 2πR, высота прямоугольника равна высоте цилиндра. Разверт! кой прямого кругового конуса является сектор окружности, радиус которой равен натуральной длине образующей l, а ϕ = 360°·R/l.

Но можно по дуге отложить столько хорд, сколько сторон име! ет вписанный в окружность многоугольник. Чтобы построить развертку наклонного конуса (рис. 164), можно вписать в него 12!угольную пирамиду и последовательно строить треугольники по трем сторонам, предварительно определив натуральную вели!

				Т е м а 8. Образование поверхностей, их классификация...									133
							S2
									НВ SB
							i2
X12												82′
	7	2			102		1
							2
			51		41		S1 ≡i1	11′	41′	51′	6 ′ 7 ′
					31						1	1
6							21′	31′121′ 111′ 101′ 91′ 81′
	1					21
71							11					S
81							121
			91		101	111	1					НВ S1
							2
							3
							4						1
							5					12
							6					11 НВ
								7		9		10
									8
							Рис. 164

чину каждого ребра пирамиды способом прямоугольного треуголь! ника, или способом вращения образующих вокруг оси i π1 до по! ложения, когда образующие расположатся параллельно фронталь! ной плоскости проекций (S111 || Х12). При этом все точки основания перемещаются в горизонтальной плоскости проекций, поэтому новые фронтальные проекции точек 1′2, 2′2... будут ле! жать на оси Х12. Затем строится развертка, состоящая из треуголь! ников 1S2, 2S3, 3S4...

Указания. После изучения информации следует вернуться к вопросам и задачам 57–60.

134 Р а з д е л 1. Ортогональные проекции

ПРОВЕРКА ЗНАНИЙ

Необходимо выбрать или сконструировать ответ. Буквенные обо значения ответов записать в таблицу, вычерченную в тетради.

	Вопросы	1	2			3			4
				1 гр	2 гр	3 гр	4 гр	5 гр
	Ответы

1.Многогранной называется поверхность, образованная... пря мой линии по... направляющей.

а) кривой; б) вращением; в) движением; г) прямой; д) ломаной.

2.Разверткой поверхности называется... фигура, образованная последовательным... всех плоских элементов этой поверхности с...

без складок и разрывов.

а) движением; б) пространственная; в) плоская; г) совмещением; д) плоскостями; е) одной плоскостью.

3.Перечисленные кривые поверхности сгруппировать по их при знакам.

1!я группа — линейчатые развертываемые поверхности; 2!я группа — линейчатые неразвертываемые поверхности;

3!я группа — криволинейные неразвертываемые поверхности; 4!я группа — поверхности вращения; 5!я группа — геликоиды:

а) тор;	е) коническая;
б) винтовой коноид;	ж) косой цилиндр с тремя
в) гиперболический	направляющими;
параболоид;	з) параболоид;
г) эллипсоид;	и) шар;
д) торс;	к) однополостный
	гиперболоид.

4. На каком чертеже получится в сечении конуса плоскостью α фигура в виде гиперболы? (рис. 165)

Т е м а 8. Образование поверхностей, их классификация...						135
	απ	2			απ2
		απ2			απ2
X12
απ1			απ1	απ1	απ1
а		б		в	г
			Рис. 165

ПРОВЕРКА УМЕНИЙ

Необходимо решить контрольные задачи.

Задача 61. Построить проекции сечения тора плоскостью α (рис. 166).

	απ
	2
X12	X12
απ1	απ1

а

б

Рис. 166

136	Р а з д е л 1. Ортогональные проекции		Т е м а 8. Образование поверхностей, их классификация...	137
Задача 62. Построить фронтальную проекцию линии среза по!			Задача 64. Построить три вида и развертку жестяной конструк!
верхности вращения плоскостями α и β (рис. 167).			ции (рис. 169).

106

R50

R70

84

40

βπ3

απ3

40		14				50

Рис. 167

Задача 63. Построить три вида конуса с вырезом (рис. 168).

Рис. 169

Задача 65. Построить три вида цилиндра и проекции линии пересечения цилиндра плоскостью α (рис. 170).

απ2

Рис. 168

Рис. 170

138 Р а з д е л 1. Ортогональные проекции

Òåìà 9. ПЕРЕСЕЧЕНИЯ ПРЯМОЙ

С ПОВЕРХНОСТЬЮ

ЗАДАНИЕ

1. Ответить на вопросы для самопроверки.

1.Как называются точки пересечения прямой с поверхностью?

2.По какому плану решается задача на определение точек пе! ресечения прямой с поверхностью?

3.Какие плоскости используются при построении точек пере! сечения прямой с призмой и пирамидой?

4.Какие плоскости целесообразны при построении точек пе! ресечения прямой с конусом и цилиндром?

5.Как задать вспомогательную плоскость, проходящую через данную прямую, чтобы в сечении конуса получился тре! угольник (или рассечь конус по образующим)?

6.Когда плоскость параллельна прямой?

7.Как задать вспомогательную плоскость, проходящую через данную прямую, чтобы в сечении цилиндра получить четы! рехугольник (или рассечь цилиндр по образующим)?

8.Что называется следом плоскости?

9.Какие точки содержит след плоскости?

10.Какие прямые плоскости параллельны следу плоскости?

2.Решить в тетради следующие задачи.

Задача 66. Построить горизонтальный след плоскости α, за!

данной точкой S и прямой АВ (рис. 171).

S2

A2
X12	B2
A1	S1
	B1
	Рис. 171

	Т е м а 9. Пересечение прямой с поверхностью		139
Задача 67. Построить фронтальный след плоскости β, прохо!
дящей через прямую АВ параллельно прямой m (рис. 172).
	A2
	m2
		B2
	X12
	m1	B1
	A1
	Рис. 172
Задача 68. Построить точки пресечения прямой а с поверхнос!
тью данного цилиндра (рис. 173).
	a2	a2
a2
X12
		a1
1
a
	a1
а	б	в
	Рис. 173