Курсовые задания

WBAв

–2

WBв

–2

ε2

=

= 4,59 с

;

ε4

=

=13,6 с .

l4

l2

Ответ: VA = 2,4 м/с;

VB =1,94

м/с;

VD =1,73

м/с;

ω2 =1,9 с–1;

ω3 =1,22 с–1;

ω4 = 2,43 с–1;

WA = 9,6 м/с2; WB =11,9 м/с2;

ε2 = 4,59 с–2;

ε4 =13,6 с–2.

ДИНАМИКА

Задание Д1

ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ, НАХОДЯЩЕЙСЯ ПОД ДЕЙСТВИЕМ ПЕРЕМЕННЫХ СИЛ

Груз D массой m, получив в точке А начальную скорость ϑ0 , движется в трубе АВ, расположенной в вер-

тикальной плоскости под углом α к горизонту. В точке В, находящейся на высоте h, груз начинает свободное движение (рис. Д1.0 – Д1.9, табл. Д1).

На участке АВ на груз, кроме силы тяжести, действует постоянная сила Q и сила сопротивления среды R, зависящая от скорости ϑ груза (направлена против движения), трением пренебречь.

Свободное движение происходит под действием силы тяжести в поле, воздействующем на точку силой F , или переменной силы притяжения к центру О, которая пропорциональна расстоянию от точки (коэффициент пропорциональности с).

Таблица Д1

	Номер	m,	ϑ0,	Q,	R, Н	l,	t1,	h,	а,	b,	с,	F, Н
	условия	кг	м/с	Н		м	с	м	м	м	Н/м
	0	4	15	3	0,4ϑ2	3	–	5	3	2	150	–
	1	3	18	11	0,2ϑ	–	3	2	4	1	200	–
	2	2,5	14	7	0,8ϑ2	2,5	–	4,5	–	–	–	3cos 5t
	3	1,3	21	9	0,9ϑ	–	1,5	3	–	–	–	2 sin 4t
	4	2	17	15	0,7ϑ2	4	–	2,5	1	3	450	–
	5	3,8	20	4	0,3ϑ	–	2	6	4	6	180	–
	6	4,5	23	10	0,1ϑ2	1,5	–	6,5	–	–	–	cos 6t
	7	5	19	8	0,5ϑ	–	2,5	1	–	–	–	4 sin 5t
	8	5,7	22	14	0,2ϑ2	2	–	8,3	3	5	370	–
	9	1,6	13	6	0,7ϑ	–	4	7	–	–	–	8 sin t

Рис. Д1.0

Рис. Д1.1

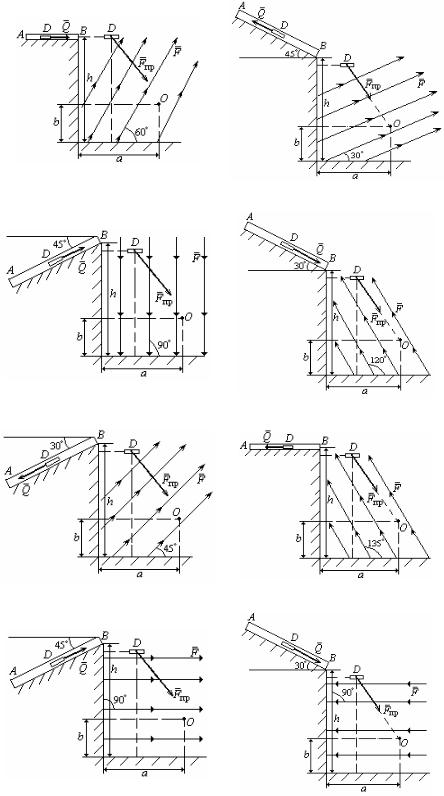
Рис. Д1.2

Рис. Д1.3

Рис. Д1.4

Рис. Д1.5

Рис. Д1.6

Рис. Д1.7

Рис. Д1.8

Рис. Д1.9

Считая груз материальной точкой и зная расстояние AB = l или время t1 движения груза от точки А до точки В, определить в координатной форме закон движения точки D на участке свободного падения.

Методические указания

При выполнении задания Д1 необходимо изучить темы: «Основные законы динамики материальной точки», «Дифференциальные уравнения движения материальной точки». При этом рекомендуется разобрать пример решения и решить самостоятельно следующие задачи: [1, т. 2 – 8.17, 8.19, 8.22, 8.26]; [6 – Д1, Д2]; [5 – 27.17, 27.22, 27.31].

При решении задания рекомендуется придерживаться следующей последовательности:

1)выбрать систему координат. При прямолинейном движении точки – координатная ось направлена в сторону движения точки с началом отсчета в начальном положении точки. При плоском движении – плоская система координат xy;

2)движущуюся точку изобразить в текущем положении при положительных значениях координат;

3)показать все действующие на точку силы;

4)определить сумму проекций действующих сил на выбранные оси координат;

5)записать дифференциальные уравнения движения материальной точки в проекциях на оси координат;

6)найти общие решения дифференциальных уравнений. В качестве методов решения дифференциальных уравнений могут быть выбраны либо метод понижения порядка, либо метод решения линейного неоднородного дифференциального уравнения второго порядка;

7)составить начальные условия движения материальной точки, т.е. значения координат и проекций скорости точки на координатные оси в начальный момент времени;

8)определить постоянные интегрирования по начальным условиям движения;

9)записать закон движения точки с учетом найденных постоянных;

10)составить конечные условия (если это необходимо) и определить искомые величины.

Если движение точки рассматривается на двух участках, то ее скорость в конце первого участка будет являться начальной при движении на втором.

Пример решения задания Д1

На наклонном участке АВ трубы (см. рис. Д1) на груз D массой m действуют сила тяжести и сила сопротивления R; время движения точки на этом участке, где начальная скорость ϑ = ϑ0 , равно t1 . Свободное дви-

жение происходит под действием силы тяжести и силы притяжения к центру О.

Рис. Д1

Дано: m = 2 кг, R = µϑ, µ = 0,1 кг/м, ϑ0 =12 м/c, t1 = 2 с, Fпр = cr , где r – расстояние от точки до центра притяжения; a = 3 м, b = 4 м, h = 5 м. Определить закон свободного движения точки в форме x = f1(t), y = f2 (t).

Решение

1 Рассмотрим движение груза на участке AB, считая груз материальной точкой. Так как движение на участке прямолинейное, то системой координат является ось z. Начало отсчета помещаем в точку начала движения. Тогда текущее положение груза на оси определится координатой z. Действующими силами являются

P = mg , R и N .

Составим дифференциальное уравнение движения груза в проекции на эту ось

m

dϑz

= ∑Fkz .

(1)

dt

Определяем проекции действующих сил на

выбранную ось координат:

Pz −mg sin α ,

Rz = −R = −µϑ

(ϑ = ϑz ), Nz = 0 . Таким образом, получим

dϑ

dϑ

µ

gm

m

= −mg sin α −µϑ

или

= −

sin α +ϑ .

(2)

dt

dt

µ

m

Введем для сокращения записей обозначения:

k = −

µ

= −0,05 с–1,

n =

gm

sin α =100

м/с, где при расчетах

m

µ

принято g ≈10 м/с2. Тогда уравнение (2) представляется в виде

dϑ

= k(n +ϑ).

(3)

dt

Разделяя в уравнении (3) переменные и интегрируя, получим общее решение дифференциального уравне-

ния

	dϑ	= kdt , ln		n +ϑ		= kt +C .	(4)
	n +ϑ					1

Составим начальные условия для определения C1 : при t = 0 , ϑ = ϑ0 . Подставим в решение (4), получим

C1 =ln n + ϑ0 .

Частное решение дифференциального уравнения, описывающего движение точки на участке АВ, принима-

ет вид:

n +ϑ

n + ϑ

ln

n +ϑ

= kt + ln

n + ϑ0

, ln

= kt ,

= ekt .

Окончательно

n +ϑ0

n + ϑ0

ϑ = (n +ϑ0 )ekt −n .

(5)

Составим условия для определения ϑ1 на границе трубки (в точке В): t = t1 , ϑ = ϑ1 . Подставив их в решение (5), получим

ϑ1 = (n +ϑ0 )ekt1 −n .

Заменим k и n их значениями ( t1 = 2 с, ϑ0 =12 м/с):

ϑ1 = (100 +12)e−0,05 2 −100 =1,34 м/с.

2 Рассмотрим свободное движение груза. Движение груза происходит в плоскости. Поэтому выберем плоскую систему координат xy так, как показано на рис. Д1. Тогда текущее положение груза в плоскости опре-

делится координатами x и y. Покажем действующие силы: силу тяжести P = mg , силу притяжения

– расстояние до центра притяжения.

Составим дифференциальные уравнения движения груза в проекциях по осям координат

mx = Px + Fпр x ;

my = Py + Fпр y .

Проекции действующих сил на координатные оси имеют вид

			Px = 0 ;		Fпр x = cr cos α ;		Py = −P ; Fпр y = cr sin α ,
где cos α =	a − x	, sin α =	y −b	. Или:	F	= c(a − x), F		= c(y −b).
	r		r		пр x	пр y

Таким образом, получим

mx = c(a − x);my = −P −c(y −b). .

Fпр = cr , r

(6) – (7)

Рассмотрим дифференциальное уравнение (6), которое представим в виде

x +k 2 x = h ,	(8)
1

где k 2 = mc =1 с–2; h1 = cam = 3 м/с2.

Из теории дифференциальных уравнений известно, что решение такого неоднородного уравнения ищется в виде

	~	*	,
	x = x + x
~							*	– частное решение.
где x – решение соответствующего однородного дифференциального уравнения, а x
~	= C1 cos kt +C2 sin kt ,			x	*	= A .
x

После подстановки частного решения в (8) получим значение A = kh12 . Таким образом

x* =	h1	= 3 ;
	k 2
		x = C	cos kt +C	2	sin kt +	h1	.	(9)
		1				k 2

Для определения постоянных C1 и C2 продифференцируем (9) по времени

x = −C1k sin kt +C2k cos kt .

(10)

Составим начальные условия: t = 0 , x = 0 , x = ϑ1x

= ϑ1 cos α . Подставив в (9) и (10), получим

0 = C

+

h1

;

ϑ cos α = C

2

k .

k 2

1

Отсюда C

= −

h1

= −3 ; C

2

=

ϑ1 cos α

=1,16 .

1

k 2

k

Таким образом:

x = −3cos t +1,16sin t +3 .

Рассмотрим дифференциальное уравнение (7), которое представим в виде

y +k

2 y = h ,

2

k 2 =

c

=1

с–2,

h =

cb −mg

= −6 м/с2.

m

2

m

Дальнейший расчет аналогичен приведенному выше

~

*

h2

y = y + y

= C3 cos kt +C4 sin kt +

;

k 2

y = −C3k sin kt +C4k cos kt .

Начальные условия: t = 0 ,

y = h = 5 , y = ϑ1y = ϑ1 sin α . Таким образом,

h = C

3

+

h2

;

ϑ sin α = C

4

k .

k 2

1

Отсюда C

= h −

h2

=11 ;

C

4

=

ϑ1 sin α

= 0,67 .

3

k 2

k

Окончательно,

y =11cos t +0,67 sin t −6 .

Задание Д2

ПРИМЕНЕНИЕ ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА К ОПРЕДЕЛЕНИЮ УГЛОВОЙ СКОРОСТИ ТВЕРДОГО ТЕЛА

Материальное тело массы m1 в виде прямоугольного параллелепипеда с линейными размерами a, b, c или кругового цилиндра с высотой h и радиусом основания r вращается с угловой скоростью ω0 вокруг вертикаль-

ной оси, проходящей через боковое ребро (параллельно ему) параллелепипеда или образующую (параллельно ей) цилиндра (рис. Д2.0 – Д2.9).

В некоторый момент времени t = 0 относительно тела под действием внутренних сил начинает движение материальная точка М массы m2 по прямолинейной направляющей по закону sr = OM = f (t) в плоскости бо-

ковой грани или диагонального сечения параллелепипеда или осевого сечения цилиндра. При этом на тело действует сила F , расположенная в плоскости, перпендикулярной оси вращения.

Точки приложения силы F , которыми могут быть вершины, середины сторон граней параллелепипеда или вершины осевых сечений цилиндра; углы α и β, составляемые вектором силы с положительными направлениями осей x и y; зависимость величины силы от времени указаны в табл. Д2. Направления осей координат x, y, z и размеры a, b, c для всех соответствующих вариантов показаны на рис. Д2.0.

Материальная точка М на рисунке показана в положении, когда sr > 0 . Если sr < 0 , то точка находится по

другую сторону от точки О. Точка О является серединой диагонали боковой грани или диагонального сечения параллелепипеда или осевого сечения цилиндра.

Найти угловую скорость тела в момент времени t1 , когда точка М будет находиться в соответствующей

вершине параллелепипеда или осевого сечения цилиндра.

При расчетах принять: m1 = 40 кг; m2 =10 кг; a = 2 м; b = 2,5 м; c = 3 м; h = 2 м; r =1 м; ω0 = 5 с–1.

Методические указания

Перед выполнением задания Д2 необходимо изучить тему «Момент количеств движения материальной системы», при этом рекомендуется разобрать пример решения и решить самостоятельно следующие задачи: [1,

т. 2 – 9.43, 9.45, 9.56], [6 – Д9], [5 – 37.43, 37.52, 37.56].

При решении задачи целесообразно придерживаться следующей последовательности:

1)записать теорему об изменении главного момента количеств движения (кинетического момента) системы материальное тело – точка относительно оси, совпадающей с неподвижной осью вращения тела;

2)определить кинетический момент системы относительно оси как алгебраическую сумму моментов тела

иматериальной точки относительно этой оси, учитывая, что кинетический момент точки равен алгебраической сумме ее кинетических моментов в относительном и переносном движениях;

3)вычислить алгебраическую сумму моментов (главный момент) внешних сил и пар сил системы относительно указанной оси, показав эти силы на чертеже;

4)определить кинетический момент системы в начальный момент времени, т.е. начальные условия для дифференциального уравнения, записанного в п. 1;

5)проинтегрировать дифференциальное уравнение п. 1 и определить постоянную интегрирования, используя начальные условия п. 4;

6)определить из равенства, полученного в п. 5, угловую скорость тела как функцию времени и ее значе-

ние в момент времени t1 .

Момент инерции тела относительно оси вращения следует определять из равенства

J z = J zc′ + m1d 2 ,

где J zc′ – момент инерции относительно оси, параллельной оси вращения и проходящей через его центр масс; m1 – масса тела; d – расстояние между указанными осями.

Момент инерции прямоугольного параллелепипеда относительно оси, параллельной оси вращения и проходящей через центр масс

J c′ = m1(a2 +b2 ), z 12

где a и b – длины сторон основания. Для кругового цилиндра

J zc′ = m12r 2 ,

где r – радиус основания.

Таблица Д2

	Номер	Точка при-	Зависимость вели-	Углы, град		sr = OM = f (t)
	условия	ложения	чины силы F от
				α	β
		силы F	времени, Н
0		B	t3 + 2t 2 +10	120	30	0,4t3/ 2
1		D	t 2 +t + 20	30	60	−0,2t 2
2		H	t3 + 4t 2 +15	135	45	0,16t3
3		C	4t 3 +3t + 25	60	150	−0,1t 4
4		E	3t 2 +t +30	30	120	1,5t 2
5		B	2t + 40	45	45	−0,8t3/ 2
6		D	2t 3 −t +35	150	120	0,5t 4
7		H	60 −2t	60	30	−0,4t3
8		C	6t 2 +50	45	135	0,25t3/ 2
9		E	t 3 + 45	135	135	−0,6t 2

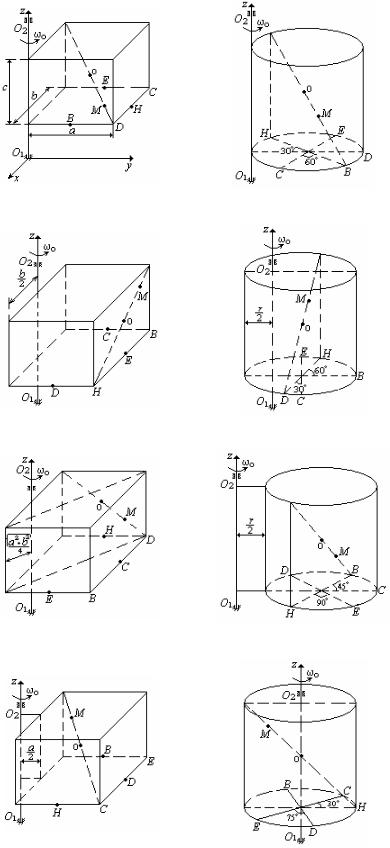
Рис. Д2.0

Рис. Д2.1

Рис. Д2.2

Рис. Д2.3

Рис. Д2.4

Рис. Д2.5

Рис. Д2.6

Рис. Д2.7

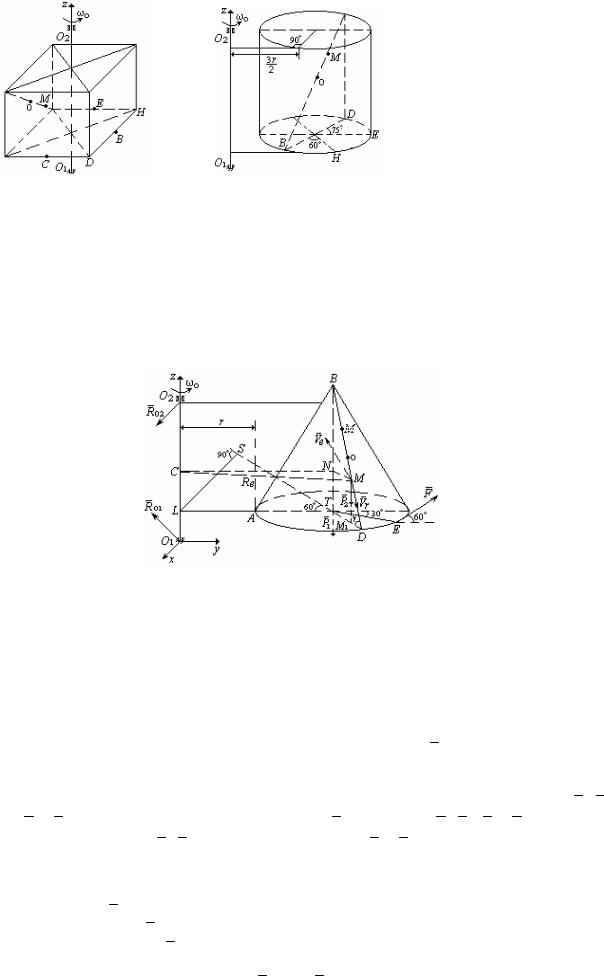
Рис. Д2.8

Рис. Д2.9

Пример решения задания Д2

Материальное тело в форме кругового конуса с высотой h и радиусом основания r, имеющее массу m1 , вращается вокруг вертикальной оси z с угловой скоростью ω0 (рис. Д2).

В момент t0 = 0 на тело в точке Е начинает действовать переменная сила F, расположенная в плоскости,

перпендикулярной оси вращения, и составляющая углы α и β с положительными направлениями осей x и y. Одновременно под действием внутренних сил относительно тела по образующей BD начинает движение материальная точка М массой m2 по закону sr = OM = f (t) (точка О является серединой образующей BD). Найти

угловую скорость тела в момент времени t1 , когда движущаяся точка М будет находиться в точке D тела.

Рис. Д2

Дано: m = 30 кг;	m	2	= 5 кг; r = 0,5 м; h = 1 м;	ω	0	= 3 с–1; F = t 4 +50 Н; s	r	= −0,3t 2	м; α = 150°; β =
1

60°.

Определить: ω1 – угловую скорость тела в момент времени t1 .

Решение

Для определения угловой скорости тела применим теорему об изменении кинетического момента системы относительно оси z, состоящей из тела и материальной точки М

	dK z		= ∑M z (	Fke ).	(1)
	dt
Изображаем в текущем положении материальную точку М,			учитывая, что переменная		величина

sr = OM < 0 , и показываем действующие на систему внешние силы, которыми являются силы тяжести P1 , P2 , реакции R01 , R02 подпятника и подшипника и заданная сила F . Моменты сил P1 , P2 , R01 , R02 относительно оси z равны нулю, так как силы P1 , P2 параллельны оси z, а реакции R01 , R02 пересекают ось z.

Предполагая вращение тела против хода часовой стрелки, если смотреть со стороны положительного направления оси z, принимаем это направление за положительное при установлении знаков кинетических моментов тела и материальной точки.

Раскладывая силу F на составляющие по осям x и y и используя теорему Вариньона о моменте равнодействующей, для момента силы F относительно оси z получим:

M z (F )= F cos 60D r sin 30D + F cos 30D(2r + r sin60D);

∑M z (Fke )= M z (F )= F hz ,

где hz = r(1+ 2 cos 30D)≈1,35 м.

Уравнение (1) может быть записано в виде

	dK z	= hz (t 4 +50).	(2)
	dt
Кинетический момент системы равен
	K z	= K zт + K zм ,	(3)

где K zт , K zм – кинетические моменты относительно оси z тела и материальной точки соответственно.

Тело совершает вращательное движение вокруг оси z, поэтому K zт = J z ω. Момент инерции тела относи-

тельно оси z определяется по теореме Гюйгенса о зависимости между моментами инерции относительно параллельных осей:

			J	z	= J с	+ m LT 2 .
					z′	1
	В данном случае J zс′ =	3m r 2					43m r 2
		1	, LT = 2r . Тогда момент инерции K z =				1	, а кинетический момент тела
		10					10

K zт = 43m1r 2ω . 10

При определении кинетического момента материальной точки ее движение рассматривается как сложное; при этом относительным движением является ее движение по прямой BD по отношению к телу, а вращение тела вокруг оси z для материальной точки является переносным движением.

Абсолютная скорость материальной точки V =Vr +Ve .

Относительная скорость точки Vr = dSdtr = −0,6t .

Так как Vr < 0 , то точка движется в направлении к точке D. С учетом этого, изображаем вектор Vr на чер-

теже.

Определим кинетический момент точки относительно оси z в ее относительном движении

M z (m2Vr )= −m2 Vr cos γ SL ,

где cos γ =	r	≈ 0,45 ; SL = LT sin 60D = 2r sin 60D ≈ 0,87 м.
	r 2 + h2

Определим кинетический момент точки относительно оси z в ее переносном движении. Изображаем вектор переносной скорости точки Ve с учетом направления угловой скорости ω. Так как вектор Ve перпендикуля-

рен к отрезку Re , который является расстоянием от точки до оси вращения, и к оси z, то для M z (m2Ve ) получим

Re2 = CM 2 = LM12 = LT 2 +TM12 −2LT TM1 cos120D =

2

r

2

r

D

=

4r

+

+

sr

cos γ

+4r

+

sr

cos γ sin 30

=

2

2

21r 2

2

2

=

+3r

sr

cos γ + sr

cos

γ.

4

По теореме Вариньона кинетический момент материальной точки относительно оси z в ее абсолютном движении равен

K zм = M z (mV )= M z (m2Vr )+ M z (m2Ve )=

21r 2

2

2

= −m

2

V

r

cos γ SL + m

ω

+3r

s

r

cos γ + s

r

cos

γ .

2

4

Кинетический момент материальной системы согласно равенству (3) равен

43m r 2

21r 2

K

=

1

+m

+3r

s

cos γ + s

2cos2 γ

ω−m

V

cos γ SL .

(4)

z

10

2

4

r

r

2

r

Определим кинетический момент системы в начальный момент времени t = 0 ,

когда

ω = ω0 , sr

= 0 ,

Vr

= 0 :

43m

21m

2

K z0

=

1

+

r 2ω0 .

(5)

4

10

Начальные условия движения для дифференциального уравнения (2) имеют вид: t = 0 ,

K z = Kz0 , где ве-

личина Kz0

определяется в соответствии с равенством (5).

Разделяя переменные в уравнении (2) и интегрируя обе части полученного равенства, запишем его общее

решение в виде

t5

K

z

= h

+50t

+C .

(6)

z

5

Постоянная интегрирования C определяется по начальным условиям движения: C = K z0 . Подставляя зна-

чение постоянной в равенство (6) и заменяя в нем Kz ,

K z0

согласно (4) и (5), получим

43m r 2

21r 2

1

+m

+3r

s

cos γ + s2cos2 γ

ω−m

V

cos γ SL =

10

2

4

r

r

2

r

t5

43m

21m

2

= h

+50t

+

1

+

r 2ω

0

.

z

5

10

4

С учетом данных задачи и величин, определяемых в процессе ее решения, из этого равенства находится

зависимость угловой скорости тела от времени:

ω =

0,27t5 +67,5t +116,46

.

(7)

0,09t 4 +1,01t 2 +

38,82

Момент времени t1 ,

когда материальная точка М находится в точке D тела, определяется из равенства

sr

= OD =

r

:

2 cos γ

t1 =

r

≈1,85

с.

0,6 cos γ

Подставляя

t1 в правую часть равенства (7), находим угловую скорость тела в этот момент времени

ω1 = 5,71 с–1.

Ответ: ω1 = 5,71 с–1.

Задание Д3

ПРИМЕНЕНИЕ ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ К ИЗУЧЕНИЮ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Механическая система, включающая грузы 1, 3, ползун 2, ступенчатый шкив, блок, каток 4, 5, 6 и кривошип 7 длиной l, начинает движение из состояния покоя под действием силы F, зависящей от перемещения s точки ее приложения или являющейся постоянной, и пары сил с моментом M B , который является функцией

угла поворота соответствующего тела или постоянный (рис. Д3.0 – Д3.9).

Содним из тел системы связана пружина, коэффициент жесткости которой равен с, а соединение тел друг

сдругом осуществляется нитями, параллельными соответствующим плоскостям, и шарнирами. Деформация

пружины в начальном положении механической системы, в котором кривошип занимает положение B0 D0 ,

равна нулю.

Определить значение величины, указанной в последнем столбце табл. Д3, в конечном положении системы, в котором кривошип занимает положение, указанное на рисунке. Предполагается, что движение катков по