
8.5. Интегралы вида
а)
![]()
b)
![]()
с)

d)
Интегралы а) и с) приводятся к табличным интегралам 11-14 (см.8.1) путем выделения полного квадрата в квадратном трехчлене.
При вычислении интегралов типа b) иd) могут возникать две ситуации:
если выражениеMX+N является производной от квадратного трехчленаax2 + bx + c, то интегралыb) иd) берутся по формулам (2) и (1) в п.8.1 соответственно;
если же выражениеMX+ Nне совпадает с производной трехчленаax2 + bx + c, то его следует преобразовать так, чтобы из него можно было выделить производную трехчлена. После этого каждый из интеграловb) иd) представляются в виде суммы двух интегралов, один из которых берется по формулам (2) или (1), а другой есть интеграл типа а) и с).
Найти интегралы:
а)
![]()
Так как x2 + 2x + 10 = x2 + 2x + 1 + 9 = (x + 1)2 + 32, то

b)
![]()

![]()
с)

d)


![]()
Задание 8.5.Найти интегралы:
1.
![]() 2.
2.![]()
3.
![]() 4.
4.![]()
5.
![]() 6.
6.![]()
7.
![]() 8.
8.![]()
9.
![]() 10.
10.![]()
11.
![]() 12.
12.![]()
13.
![]() 14.
14.![]()
15.
 16.
16.
17.
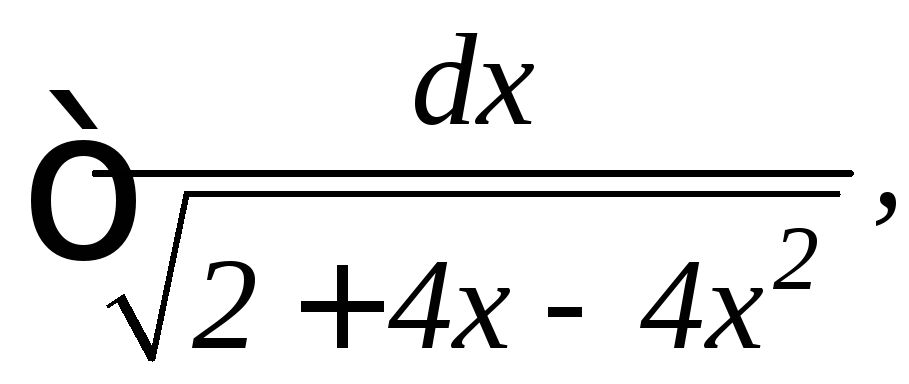 18.
18.
19.
 20.
20.
21.
 22.
22.
23.
 24.
24.
25.
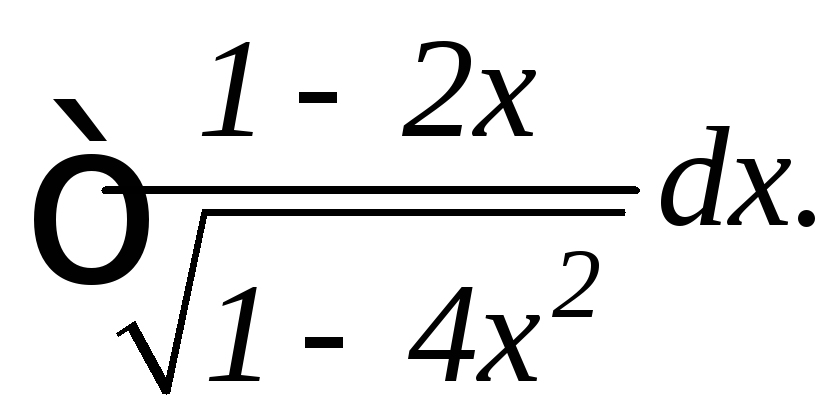
К интегралу вида (d) приводится также интеграл вида

Для этого достаточно воспользоваться
подстановкой
![]()
Пример. Найти интеграл

Решение.
Положим
![]() тогда
тогда![]()




Найти интегралы:
1.
 2.
2.
3.
 4.
4.
5.
 6.
6.
7.
 8.
8.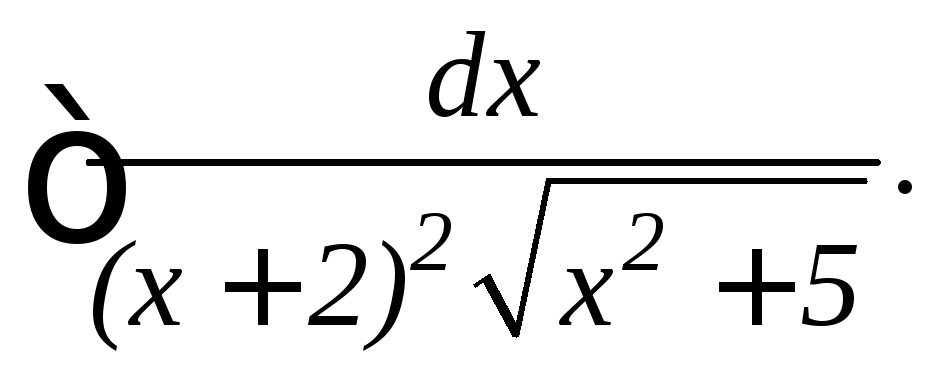
8.6. Интегрирование рациональных дробей
Дроби следующих четырех типов называются простейшими:
I.
![]()
II.

III.
![]()
IV.
где m, n– натуральные числа, аax2 + bx + c не имеет действительных корней.
Интегрирование дробей первых двух типов производится непосредственно, а интегрирование дробей третьего типа рассмотрено в подразделе (8.5.). Интегрирование дроби четвертого типа связано с применением рекурентной формулы вида
 .
(8.1)
.
(8.1)
Пример. Найти интеграл.


 гдеt = x
– 2.
гдеt = x
– 2.
По рекурентной формуле находим интеграл, полагая n = 2

Интегрирование произвольной рациональной дроби
 с действительными коэффициентами
производится следующим образом:
с действительными коэффициентами
производится следующим образом:
если m<n, то дробь называетсяправильной,
если же m ≥ n,то дробь![]() -неправильная и ее необходимо
представить в виде суммы целой части и
правильной рациональной дроби,
-неправильная и ее необходимо
представить в виде суммы целой части и
правильной рациональной дроби,
т. е.
 гдеLm
– n(x)
иRr(x)– многочлены степенейm
– n ≥ 0иr
соответственно, причемr
≤ n,
гдеLm
– n(x)
иRr(x)– многочлены степенейm
– n ≥ 0иr
соответственно, причемr
≤ n,
т. е.
![]() - правильная.
- правильная.
Выделение целой части в дроби
![]() производится делением числителя на
знаменатель «уголком».
производится делением числителя на
знаменатель «уголком».
Пример.Выделить целую часть дроби
 .
.
Делим числитель на знаменатель таким образом
x4 –3x2 –3x – 2 | x3 – x2 –2x
- | __________
x4 – x3 –2x2 | x + 1
______________
x3 – x2 –3x – 2
-
x3 – x2 –2x
______________
- x – 2 .
Следовательно,
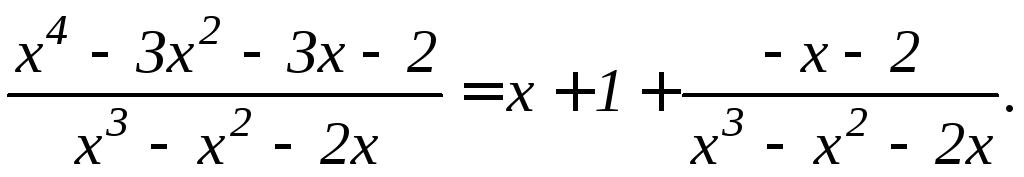
Пусть Qn(x)есть многочлен степениnс действительными коэффициентами вида
![]() .
.
Известно, что всякий многочлен разлагается единственным образом на линейные и квадратичные множители вида (x - a) и(x2 + px + q), гдеa– действительный корень многочлена, квадратный трехчленx2 + px + q не имеет действительных корней, т. к.

В общем виде разложение многочлена Qn(x) имеет вид
![]() (*)
(*)
где a иb – действительные корни кратностиk иm соответственно, аr иsвыражают кратность каждой пары сопряженных комплексных корней многочлена.
При этом справедливо равенство:
![]()
Имеет место следующая теорема о разложении правильной рациональной дроби на сумму простейших дробей.
Теорема. Всякая правильная
рациональная дробь![]() знаменатель которойQ(x
)имеет разложение (*), может быть
представлена единственным образом в
виде суммы конечного числа простейших
дробей следующим образом:
знаменатель которойQ(x
)имеет разложение (*), может быть
представлена единственным образом в
виде суммы конечного числа простейших
дробей следующим образом:


 .
.
Для нахождения неопределенных коэффициентов
![]()
поступают следующим образом: приравнивают коэффициенты при одинаковых степенях x у многочленаP(x) и многочлена, который получается в числителе правой части после приведения ее к общему знаменателю (метод неопределенных коэффициентов).
Продолжим рассматривать предыдущий пример

Полученную правильную дробь представим в виде суммы простейших дробей
 .
.
Приведя правую часть к общему знаменателю, получаем тождество, приравняв числители:
![]()
![]() .
.
Приравнивая коэффициенты при одинаковых степенях, получаем систему
 .
.
Откуда
![]()
Следовательно
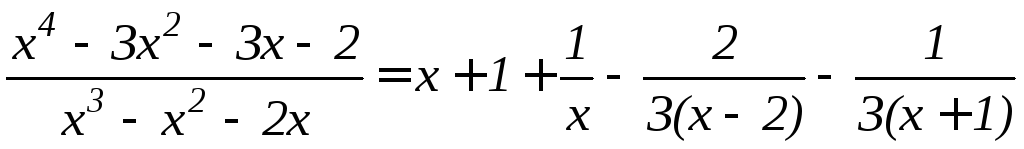
и
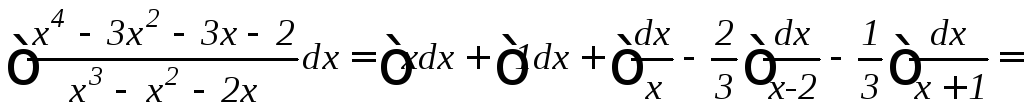
=
Пример.Найти интеграл

Дробь
 правильная, разложим знаменатель на
простейшие сомножители:
правильная, разложим знаменатель на
простейшие сомножители:![]()
Дробь
 может быть представлена в виде суммы
простейших дробей:
может быть представлена в виде суммы
простейших дробей:

Приведя простейшие дроби к общему знаменателю, и приравнивая числители, получим
![]()
![]() .
.
Приравнивая коэффициенты при одинаковых степенях x
A + B = 0
C = 1
2A + B + D = 0
C + E = 0
A = 1 .
Решая систему, находим
A = 1, B = -1, C = 1, D = -1, E = -1.
Следовательно

тогда:


 .
.
Последний интеграл находим по рекурентной формуле (8.1) при n = 2

Задание 8.6. Найти интегралы:
1.
 2.
2.![]()
3.
 4.
4.
5.
 6.
6.![]()
7.
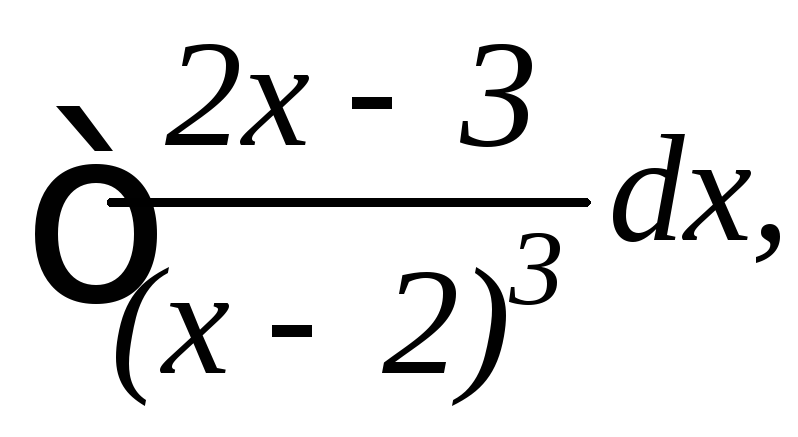 8.
8.
9.
 10.
10.
11.
 12.
12.
13.
 14.
14.![]()
15.
 16.
16.
17.
 18.
18.
19.
 20.
20.
21.
![]() 22.
22.
23.
![]() 24.
24.
25.

