
Продолжение лекции по мышцам
.docПассивное растяжение.
На основании расчетных и экспериментальных данных показано, что наиболее простой моделью, дающей достаточно хорошее приближение к механическим свойствам мышцы, является трехкомпонентная модель Хилла (Трехкомпонентная модель мышцы, где СЭ - сократительный элемент). Очень часто для того, чтобы понять механизм работы объекта, его заменяют адекватной моделью. Модель – образ объекта, который содержит его характерные черты. Вначале предполагали, что мышца может моделироваться системой, состоящей из двух компонентов: активного и пассивного. Сократительный (активный) элемент уподоблялся демпфирующему компоненту. Пассивный элемент представлялся упругим компонентом. В последующем Хилл предложил модель мышцы, состоящую из трех компонентов, которая в настоящее время является общепринятой:
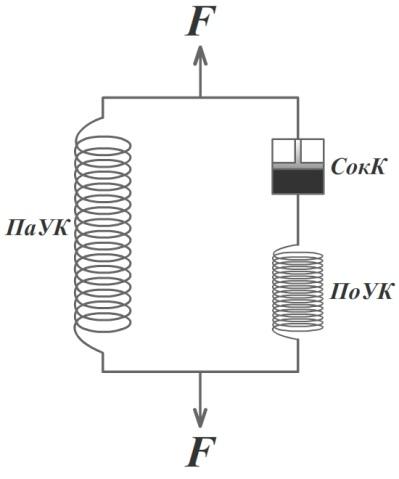
Рис. 5. Трехкомпонентная модель мышцы.
Выделяют три компонента: мышечные волокна, соединительно-тканные образования, расположенные параллельно мышечным волокнам, и сухожилия. Биомеханические свойства этих компонентов различны.
1) Мышечные волокна характеризуются высокой вязкостью, поэтому в модели их имитируют демпфером. Вязкая жидкость характеризуется прямой пропорциональностью между напряжением и скоростью деформации. Этот элемент в модели носит название сократительного компонента (СокК).
2) Второй компонент – фасция, которой окружена мышца, а также соединительно-тканные образования, окружающие мышечные пучки, мышечные волокна, миофибриллы и т.д. В этом компоненте наиболее выражены упругие свойства мышц. Так как этот компонент расположен параллельно мышечным волокнам, он получил название параллельный упругий компонент (ПаУК). В модели он имитируется пружиной с нелинейной зависимостью между силой и удлинением.
3) Третий компонент – сухожилие. В этом компоненте также преобладают упругие свойства, однако, жесткость этого компонента больше, чем у параллельного упругого компонента (напоминаем, что жесткость – это коэффициент пропорциональности между силой и удлинением пружины). Чем выше жесткость, тем больше сила упругости, возникающая при растяжении (деформации тела). Мышечные волокна переходят в сухожилия, то есть этот компонент расположен последовательно относительно сократительного компонента, поэтому он называется последовательным упругим компонентом (ПоУК). В модели он также имитируется пружиной с нелинейной зависимостью между силой и удлинением.
Используя данную модель и несколько ее упрощая (для некоторых начальных условий) можно с помощью нескольких дифференциальных уравнений вычислить характерную зависимость деформации мышцы во времени при приложении к ней воздействия:
ε (t ) = σ/ Е (1- е t/τ),
где τ = η/Е - называется временем запаздывания.
Такая зависимость достаточно хорошо описывает процесс нарастания деформации ε (t), полученный в эксперименте.
В терминах механической модели (трехкомпонентной) в применении к модели скользящих нитей:
Параллельный упругий элемент определяет механические свойства внешних мембран клеток (сарколеммы) и внутренних структур (Т-системы и саркоплазматического ретикулума).
Последовательный элемент определяет упругость актин-миозинового комплекса, обусловленную, прежде всего, местами прикрепления актина к Z-дискам и местами соединения мостиков с активными центрами тонких нитей.
Вязкий элемент η обусловлен скольжением нитей актина относительно миозина. Эта компонента резко возрастает при пассивном режиме мышцы, так как в этом случае мостики разомкнуты. Это проявляется в возможности сильного растяжения пассивной мышцы даже при незначительных нагрузках.
Активное сокращение мышцы.
Для исследования характеристик сокращающихся мышц используют два искусственных режима:
1. Изометрический режим, при котором длина мышцы l =const, а регистрируется развиваемая сила F(t).
2 .
Изотонический режим, при котором мышца
поднимает постоянный груз Р=const, а
регистрируется изменение ее длины во
времени Δ l
(t).
.
Изотонический режим, при котором мышца
поднимает постоянный груз Р=const, а
регистрируется изменение ее длины во
времени Δ l
(t).
Рис. 6. Схемы опытных установок для реализации в эксперименте изометрического (а) и изотонического (б) режимов (ДF- датчик силы, Д - датчик изменения длины, М - мышца, Эл – электроды стимуляции, Р - нагрузка, Ф - фиксатор длины).
При изометрическом режиме с помощью фиксатора (рис. 6, а) предварительно устанавливают длину мышцы l. После установки длины на электроды Э подается электрический стимул и с помощью датчика регистрируется функция F(t). Вид функции F(t) в изометрическом режиме для двух различных длин представлен на рис. 7, а.
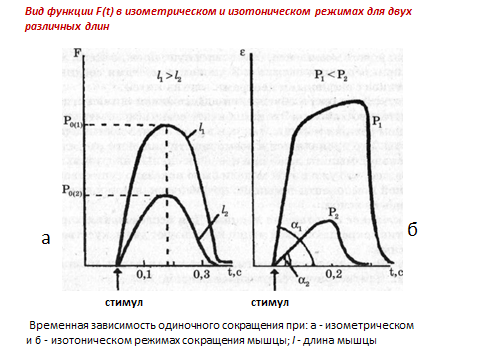
Рис. 7. Временная зависимость одиночного сокращения при: а - изометрическом и б - изотоническом режимах сокращения мышцы; l - длина мышцы.
Максимальная сила Р0, которую может развивать мышца, зависит от ее начальной длины и области перекрытия актиновых и миозиновых нитей, в которой могут замыкаться мостики: при начальной длине саркомера 2,2 мкм в сокращении участвуют все мостики. Поэтому максимальная сила генерируется тогда, когда мышца предварительно растянута на установке (рис. 6, а) так, чтобы длины ее саркомеров были близки к 2,2 мкм. На рис. 7, а это соответствует начальный длинам двух мышц 11 и 12. Но так как количество мостиков в мышце 11 больше, чем в 12 (11 > 12), то сила, генерируемая 11 больше.
При изотоническом режиме к незакрепленному концу мышцы подвешивают груз Р (рис.6, б). После этого подается стимул и регистрируется изменение длины мышцы во времени: Δ l (t). Вид этой функции в изотоническом режиме для двух различных нагрузок показан на рис.7, б.
Как следует из рис. 7.б, чем больше груз Р, тем меньше укорочение мышцы и короче время удержания груза. При некоторой нагрузке Р = Р0 мышца совсем перестает поднимать груз; это значение Р0 и будет максимальной силой изометрического сокращения для данной мышцы (рис. 7, а).
Здесь важно отметить, что при увеличении нагрузки угол наклона восходящей части кривой изотонического сокращения уменьшается (рис. 7, б): α2 < α1. Другими словами, скорость укорочения с ростом нагрузки падает.
Уравнение Хилла. Мощность одиночного сокращения.
Зависимость скорости укорочения от нагрузки Р является важнейшей при изучении работы мышцы, так как позволяет выявить закономерности мышечного сокращения и его энергетики. Она была подробно изучена при разных режимах сокращения Хиллом и представлена на рис. 8. Им же было предложено эмпирическое выражение, описывающее эту кривую:
V(P)=b(P0-P)/P+a
Это выражение называется уравнением Хилла и является основным характеристическим уравнением механики мышечного сокращения. P0 - максимальное изометрическое напряжение, развиваемое мышцей, или максимальный груз, удерживаемый мышцей без ее удлинения; b - константа, имеющая размерность скорости, а - константа, имеющая размерность силы.
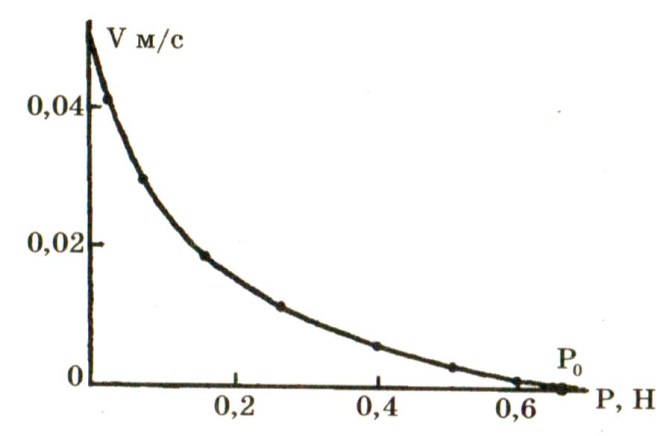
Рис. 8. Зависимость скорости одиночного сокращения мышцы от нагрузки
Из уравнения (V(P)=b(P0-P)/P+a) следует, что максимальная скорость развивается
при Р = 0:
Vmax = P0 b/a
При Р = P0 получаем V = 0, то есть укорочение не происходит. Работа А, производимая мышцей при одиночном укорочении на величину Δ1 равна:
А = РΔ1
Эта зависимость, очевидно, нелинейная, так как V = f(P). Но на ранней фазе сокращения можно пренебречь этой нелинейностью и считать V = const. Тогда
Δ1 = VΔt,
а развиваемая мышцей мощность W = dA/dt имеет вид: W = PV.
Исходя из этого, получим зависимость мощности от развиваемой силы Р:
W(P) = PV = b(P0-P)/ P+а · P
Ф ункция
W(P) имеет колоколообразную форму и
представлена следующим образом:
ункция
W(P) имеет колоколообразную форму и
представлена следующим образом:
Рис. 9. Зависимость мощности мышцы от нагрузки
Эта кривая, полученная из уравнения Хилла, хорошо согласуется с результатами опытов. Мощность равна нулю при Р = P0 и Р = 0 и достигает максимального значения при оптимальной величине нагрузки Ропт :
Ропт = √a(P0 + a)-a, то есть когда Р = 0,31 Р0.
Эффективность работы мышцы при сокращении может быть определена как отношение совершенной работы к затраченной энергии ΔЕ:
ξм= А/ΔЕ
Развитие наибольшей мощности и эффективности сокращения достигается при усилиях 0,3 - 0,4 от максимальной изометрической нагрузки Р0 для данной мышцы. Это используют, например, спортсмены-велогонщики: при переходе с равнины на горный участок нагрузка на мышцы возрастает и спортсмен переключает скорость на низшую передачу, тем самым уменьшая Р, приближая ее к Ропт. Практически эффективность может достигать значений 40 - 60 % для разных типов мышц. Самая высокая эффективность наблюдается у мышц черепахи, достигающая 75 - 80 %.
