Олимп-2010, 0.4, решения

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11апреля 2010 г.

1.(Б.М. Веретенников) Решить систему матричных уравнений

AX BY

AY BX,

где А и В – невырожденные матрицы n-го порядка, Х, Y –неизвестные, невырожденные матрицы n-го порядка.

Решение. Из первого уравнения получаем Y B 1AX . Подставляя во второе,

получим AB 1AX BX или AB 1A B X O . Таким образом, если выполнено

условие AB 1A B O , то

Х- любая невырожденная матрица. Если это условие не выполнено, то система не имеет решений.

Ответ. Если выполнено условие AB 1A B O , то Х- любая невырожденная матрица. Если AB 1A B O , то система решений не имеет.

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11 апреля 2010 г.

2. ( Г.Л.Ходак) Вычислить предел lim	1 x 10	sin x100	.
		cos x100
x 1 x 10

Решение. Так как синус и косинус являются ограниченными функциями, то предел будет равен отношению коэффициентов перед одинаковыми старшими степенями многочленов, стоящих в числителе и знаменателе, т.е. единице.

Ответ. 1.

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11апреля 2010 г.

3.(И.Ю. Андреева) Сколько существует шестизначных чисел, в записи которых есть хотя бы одна чётная цифра?

Решение. Определим сначала количество шестизначных чисел, не обладающих нужным свойством. Так как это в точности те числа, в записи которых встречаются только нечётные цифры, то их количество равно 56 15625 . Всего шестизначных чисел 900000. Поэтому количество шестизначных чисел, обладающих указанным свойством равно

900000-15625=884375.

Ответ. 884375.

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11 апреля 2010 г.

4. (Е.Г. Полищук) Пусть функция f x - непрерывна на a,b , x1,x2,...xn -

произвольные точки из a,b . Доказать, что существует x0 a,b , такое, что

f x0 f x1 f x2 ... f xn . n

Решение. Пусть min x1,x2,...,xn , max x1,x2,...,xn . Рассмотрим функцию

	f x на , . Тогда
	min	f x	f x1 f x2 ... f xn					max	f x	.
	x ,			n				x ,
	Так как функция	f x1 f x2 ... f xn				непрерывна на , , то
			n
							f x1 f x2 ... f xn
	существует точка x0 , , такая что			f x0							.
								n

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11 апреля 2010 г.

sinu

x

t

v

5. (Б.М.Веретенников) Пусть g u

,

f x

g u du dv dt , где

u

x0

t0

v0

x ,t

0

,v

-фиксированные числа, v 0

. Найти f

.

0

0

0

2

Решение. Найдём последовательно все производные до третьего порядка:

Таким образом

2

Ответ. .

			f x						x v
										g u du dt	,
									t0 v0
									x
					f		x g u du ,
									v0
							f x g x .
							2
f			g
	2
				2			.

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11 апреля 2010 г.

	6. (Л.П.Мохрачева) Однородная пластинка ограничена кривой	x2		y2	1. На какое
		a2		b2

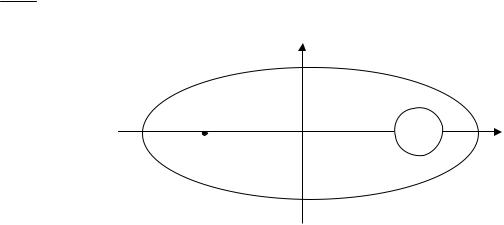
расстояние от цента сдвинется центр масс пластинки, если из неё вырезать круг радиусом

a c

, с центром в одном из фокусов?

2

Решение. Пусть круг вырезан так, как показано на рисунке

F2

.

Из-за симметрии получившейся фигуры центр масс эллипса сдвинется по оси ОХ из центра эллипса. Вычисляем новое положение центра масс

xm	xdxdy		xdxdy
	G		D							,
	dxdy			a c 2
			ab
	G				2
где ab-площадь эллипса, а область D- круг радиуса				a c				с центром во втором фокусе F .
					2			2

Стоящий в числителе интеграл удобно вычислить, если перейти к полярным координатам с полюсом в точке F2

2

a c

2

2

xdxdy d

cos c d

a c

c

.

2

G

0

0

a c 2

c

c a c

2

2

Таким образом xm

.

a c 2

4ab a c 2

ab

2

c a c 2

Ответ. Центр масс сдвинется на расстояние

влево.

4ab a c 2

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11 апреля 2010 г.

7. (Н.В. Гредасова) Доказать неравенство												1		ln		2010				1		.
										2010					2009			2009
Решение.
Способ1. Воспользуемся известным неравенством ex																		1 x,x 0 . Отсюда
следует, что если x 1 0, то ln 1 x x. Таким образом,
2010			1		1		2009			1					1		, т.е.			2010				1
ln		ln 1					и ln		ln 1											ln					.
			2009							2010					2010									2010
2009					2009		2010													2009

Способ2. Воспользуемся формулой Лагранжа ln2010 ln2009 1 2010 2009 1, 2009,2010 .

Тогда	1		1		1	и неравенство доказано.
	2010				2009

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11апреля 2010 г.

8.(Г.Л.Ходак) Вершины квадратного бильярда находятся в точках: 0,0 , 0,1 ,

1
1,0 , 1,1 . Шар запускается из точки		,0		и последовательно отражаясь от
2
сторон x 0,y 1,x 1 попадает в точку		0,0 . Чему равна длина пути шара?

Решение. Классическое рассуждение. Три раза отобразим симметрично квадрат как показано на рисунке.

По закону геометрической оптики: свет выбирает кратчайший путь, в нашем случае прямую E0 A .

	A	D		A
		E3
	B	E2			B				C
		C	E1
								E0
		D		A					D
Длину пути находим по теореме Пифагора			2	2	5 2				41	.
						2			2
Ответ.	41.
	2

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11апреля 2010 г.

9.(Н.В. Гредасова) Решить уравнение

2y y

2

y

2

y

x

.

x2 1

Решение. Заметим, что y

2

y

2

y

2

y

2

y

. Тогда

y

2yyy

2y y

2

x

1

2

y

y

1 x2

dx

2ln x

1 C1 .

2

1

3

3

3

2

3

3

2

Так как y

y

3 y

, то

y

2ln x

1 C1

и y

2

ln x

1 dx C1x C2 .

Интеграл от логарифма берём по частям

2x2

ln x

2

1 dx xln x

2

1

dx

x2 1

xln x

2

1

2x2 2 2

dx xln x

2

1 2x

2

dx

x2 1

x2 1

xln x2

1 2x 2arctgx C.

Таким образом, окончательно имеем y3 32 xln x2 1 3arctgx C1x C2 .

Ответ. y3 32 xln x2 1 3arctgx C1x C2 .

Уральский государственный технический университет – УПИ им. первого Президента России Б.Н.Ельцина

Олимпиада по математике

11апреля 2010 г.

10.(Б.М.Веретенников) Пусть fn x и gn x - многочлены степени n 1,

причём коэффициент при старшей степени у fn x положителен. Найти предел

1

lim fn x gn x .

x

Решение. Стандартным образом преобразуем предел

1

ln fn x

lim

ln fn x

lim fn x

0

lim e gn x

ex

gn x

gn x

. Стоящий в степени

x

x

предел

xlim

ln fn x

xlim

fn x

0 .

gn x

fn x g x

1

Значит

lim fn x

e0

1.

gn x

Ответ.

x

1.