Тензорная функция Грина, Яцук

СТРУКТУРА ТЕНЗОРА ГРИНА ДЛЯ ЦИЛИНДРИЧЕСКОЙ ОБЛАСТИ

Напомним, что тензорным произведением двух векторов Α и Β, определяемых компонентами Α1 , Α2 , Α3 и B1 ,B2 ,B3 , н6азывается тензор, компоненты которого строятся следующим образом:

A1B1			A1B2				A1B3
Α Β = A	2	B	A	2	B	2	A	2	B	3
		1
A	3	B	A	3	B	2	A	3	B	3
		1

Анализируя тензорные произведения собственных векторных функций в выражение (24), убеждаемся в том, что из 9 возможных компонент тензорной функции Грина от нуля отличаются всего 5, и тензор Грина имеет следующую структуру:

G11	G12	0
G (r r′)= G12	G22	0		(32)
	0
0		G33

Упражнение Расписывая подробно тензорные произведения собственных функций в

выражении (24), докажите, что тензор Грина для цилиндрической области имеет структуру, определяемую матрицей (32).

ЭЛЕКТРИЧЕССКАЯ ФУНКЦИЯ ГРИНА ПРЯМОУГОЛЬНОГО ВОЛНОВОДА

Запишем в явном виде компоненты электрической функции Грина для волновода прямоугольного поперечного сечения a ×b (a и b – размеры широкой и узкой стенок волновода). Свяжем с волноводом прямоугольную систему координат x, y,z, как показано на рис.4

20

z

b	x
	a

y

Рис.4

Найдем компоненты тензора Грина, подробно расписывая тензорные произведения в выражении (24). Электрическая функция Грина должна строиться на базе векторных функций (13), удовлетворяющих на боковой поверхности волновода тем же граничным условиям, что и электрический вектор Грина. Его тангенциальная составляющая обращается в нуль на идеальном металле, следовательно, скалярные функции χ (r ) и ψ (r ), на базе

которых строятся векторные функции (13), должны удовлетворять граничным условиям (15). А это значит, что решения уравнений (14) принимают вид:

χ mn (x, y)= sin

mπx

sin

nπy

;

a

b

(33)

ψ mn (x, y)= cos

mπx

cos

nπy

;

a

b

Поперечные собственные

числа αχ2

и αψ2 ,

сообщающие функциям

mn

mn

αχ2

(x, y)

и αψ2

(x, y) с одинаковыми индексами m,n

принимают одинаковые

mn

mn

значения

αχ2 =αψ2

mn

=α2 = (mπ a)2 +(mπ b)2

mn

mn

То же справедливо и для продольных чисел γχmn

и γψmn

γχmn = γψmn = γmn = k2 −αmn2

Поэтому функции fmn (z, z′)

и gmn (z,z′)

в выражении (24) оказываются

тождественно равными друг другу, так как они удовлетворяют, по сути, одним

21

и тем же уравнениям (23) с одинаковыми граничными условиями. Следовательно, в выражении(24) можно положить gmn (z,z′) = fmn (z,z′). Собирая с учетом всего сказанного коэффициенты при одинаковых тензорных произведениях ортов x0 , y0 ,z0

G11∂

= ∑εmεn

cos

mπx

cos

mπx′

sin

nπy

sin

nπy′

fmn (z, z′);

a

b

b

m,n

ab

a

G22∂

= ∑

εmεn sin

mπx

sin

mπx′

cos

nπy

cos

nπy′

fmn (z, z′);

(34)

b

m,n

ab

a

a

b

G33∂

= ∑

εmεn sin

mπx

sin

mπx′

sin

nπy

sin

nπy′

hmn (z, z′);

m,n

ab

a

a

b

b

G∂

= G∂

= 0.

12

21

где εm =(2 −δom );

εn =(2 −δon );

δom ,δon

– символы Кронекера.

Функции

f (z, z′) и h(z, z′) для бесконечного, полу бесконечного волноводов и резонатора определяются соответственно формулами (27), (28), 929).(30) и (31).

Как следует из (34), тензорная функция Грина прямоугольного волновода является диагональной. Это значит, что токи, совпадающие по направлению с координатными линиями, порождают векторы Герца того же направления.

Упражнения

1.Обоснуйте выбор граничных условий для скалярных функций ψ mn ,χ mn при

построении:

•Электрической тензорной функции Грина для волновода;

•Магнитной тензорной функции Грина для волновода

2.Проделайте подробный выбор формул (34), определяющих компоненты электрической функции для прямоугольного волновода.

22

МАГНИТНАЯ ФУНКЦИЯ ГРИНА ПРЯМОУГОЛЬНОГО ВОЛНОВОДА

Вслучае магнитной функции Грина граничные условия для пар функций

ψ(x, y)иχ (x, y),f (z,z′)и h (z,z′) взаимно меняются местами по сравнению

со случаем электрической функции Грина. Следовательно, и сами функции в этих парах взаимно поменяются местами.

Чтобы получить компоненты магнитной функции Грина, достаточно в выражениях для компонент электрической функции Грина произвести взаимную замену синусов и косинусов, а также функций f (z, z′) и h(z, z′).

Запишем, к примеру, выражения для компонент магнитной функции Грина бесконечного волновода:

G11M

=

2π∑εmεn sin

mπx

sin

mπx′

cos

nπy

cos

nπy′

e−iγmn (z−z′);

a

a

b

ab m,n iγmn

b

G22M

=

2π∑εmεn cos

mπx

cos

mπx′

sin

nπy

sin

nπy′

e−iγmn (z−z′);

(35)

ab m,n iγmn

a

a

b

b

G33M =

2π∑εmεn cos

mπx

cos

mπx′

cos

nπy

cos

nπy′

hmn (z, z′);

ab m,n iγmn

a

a

b

b

G∂

= G∂ = 0.

12

21

Упражнения

1.Запишите выражения компонент магнитной функции Грина для прямоугольного волновода по аналогии со случаем электрической функции Грина. Обоснуйте эту аналогию.

2.Запишите вид функций f (z, z′) и h(z, z′) в случае магнитной функции Грина для бесконечного, полу бесконечного волноводов и резонатора.

	Методические указания для
	самоконтроля
	В случае полу бесконечного волновода множитель	2π	exp{iγmn		z − z′		} в
		iγmn

выражениях (35) для G11M и GM22 следует заменить функцией h(z, z′),

определяемой формулой (29, а в выражении для G33M – функцией f (z, z′),

23

определяемой формулой (28). В случае прямоугольного резонатора следует сделать аналогичную замену, пользуясь выражениями (31) и (30) для функций h(z, z′) и f (z, z′).

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИСПОЛЬЗОВАНИЮ ТЕНЗОРНОЙ ФУНКЦИИ ГРИНА В ЗХАДАЧЕ ВОЗБУЖДЕНИЯ ПРЯМОУГОЛЬГНОГО ВОЛНОВОДА ЩЕЛЬЮ

Задание В боковой поверхности прямоугольного волновода (бесконечного, полу

бесконечного или закороченного с двух концов) прорезана узкая щель, на поверхности которой по заданному закону распределено электрическое поле. Необходимо найти электромагнитное поле, возбужденное щелью внутри волновода.

Ход выполнения задания Нужно воспользоваться теоремой эквивалентности, на основании которой

электрическое поле в щели можно заменить эквивалентным ему поверхностным током, плотность его j Μ определяется соотношением

j	Μ			(36)
		= eщ,n ,

где eщ – тангенциальная составляющая электрического поля на поверхности

щели, n - орт нормали к поверхности щели, обращенной внутрь области, где определяется поле.

Магнитный ток(36) можно рассматривать как источник электромагнитного поля, возбуждаемого щелью в волноводе. Задача сводится к нахождению с помощью функции Грина (35) магнитного вектора Герца ΠΜ , определяемого в соответствии с (8) и (36) выражением

ΠΜ =	1	∫	j M GΜ (r r′)ds	,	(37)
	4πiωμ Sщ

и дальнейшему нахождению искомых векторов Η и Ε с помощью соотношений

(3). Выражение для вектора Герца можно получить из (37), если известны геометрия системы и явный вид функцииeщ , которые определяются по – своему

в каждом конкретном случае.

Далее следует рассмотреть возбуждение бесконечного прямоугольного

24

волновода продольной и поперечной щелям. Найти в каждом из этих случаев проекцию магнитного поля на ось щели, возбуждающей это поле. Поле Η нужно искать в области волновода, находящей саму щель, т.е. в области источника.

		1. Возбуждение волновода поперечной щелью
	Свяжем с волноводом систему координат					x, y, z , а со щелью U ,V ,n ,как
показано на рис.5. Обозначим :
					a,b – размеры широкой и узкой
	0	0	z		стенок волновода,
		x			2l,d	-длина и ширина щели,
	V
		n			x0	–	смещение центра	щели
y
	x	U			относительно узкой стенке волновода.
		Рис. 5			Координаты x, y, z и −U ,V ,n
					связаны между собой соотношениями:
			U = X − X ;
			V = −z;					(38)
			n = y.
	Поле eщ представим в виде
			eщ = v0 V cos	πu ,				(39)
			d	2l
где	V – амплитудный		коэффициент,		имеющий		смысл напряжения	между

краями щели в сечении U = 0 . Такая аппроксимация поля на щели допустима в случае приблизительно полуволновых узких щелей, для которых справедливо

соотношение d 2l <<1	(0,35λ << 2l << 0,65λ).Подставим (39) в (36),находим
	j M = X 0 jΜ ,		(40)
	k
где	jx = V cos	πu .
	d	2l

25

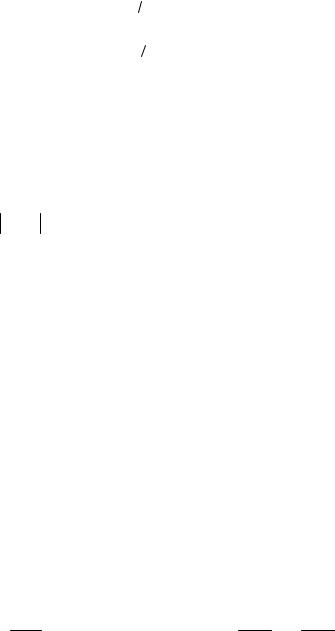
Используя это выражение для плоскости магнитного тока, перепишем выражение (37) в следующем виде:

ΠΜ = X 0ΠΜx ,

(41)

где

		V	d 2	l	πU ′
Μ			∫	∫cos			Μ	′ ′
Πx	=								(42)
		4πiωμa			2l	G11 du dv .
			−d 2 −l

В процессе интегрирования необходимо учесть, что y′ = 0 ( щель расположена в стенке, совпадающей с этой координатной поверхностью).Кроме того, в выражении для G11Μ , определяемой в (35), следует от переменных перейти к переменным U ′,V ′. При интегрировании функции, содержащей множитель exp{−iγmn z − z′}, интервал интегрирования следует разбить на два

участка: на первом интервале−z > z′ во всех точках наблюдения, поэтому интервал интегрирования разбивать не нужно.

После выполнения интегрирования не составляет принципиальных трудностей определения искомых компонент магнитного и электрического полей.

Получим в явном виде выражение для вектора Герца (41), пользуясь алгоритмом (3), можно определить искомые компоненты магнитного и электрического полей.

Приведем для примера выражение на ось щели вектора возбужденного ею магнитного поля.

V

4l

∑

ε

ε

mπx

2

mπ 2

Ηx = −

m2

n sin

0

k

−

×

a

a

iωμabd

π m,n

γmn

.

(43)

×F maπl 1−cos γmn ze−iγmn (d2) sin maπx cos mbπy

Здесь функция	F	mπl		, записанная для некоторого обобщенного аргумента η ,
	a

принимает следующий вид:

26

		F (η)=	cosη					.	(44)
				2			2
			1−		η
				π
В выражении (44) η =	mπl		εm ,εn даны в обозначениях в формуле
		. Символы
	a
(34).

Интересно отметить, что амплитудные коэффициенты при собственных функциях поперечного сечения s in maπx cos mbπy в области расположения щели довольно сложным образом зависят от координаты z . За пределами щели эта зависимость определяется множителями e iγmn z (верхний знак для z > z′, нижней - для z < z′). Такой же эффект можно будет проследить и в случае продольной щели.

2. Возбуждение волновода продольной щелью

Продольная щель длиной 2l, шириной d расположена в широкой стенке

прямоугольного волновода сечением						а × b. Тангенциальная		составляющая
0				z		электрического	поля		на	щели
			X0			определяется	выражением			(39).
						Координаты U, V,		n	связаны		с
	n		u
		v				координатами	x,	y,	z (рис.		6)
y						соотношениями:
	x
						U = z;
						v = x − x0 ;
			Рис.6							(45)
						n = y.

Магнитный ток, определяемый выражением (36), как в предыдущем случае, направлен вдоль оси щели, в данном случае вдоль оси z:

j M = z0 jzM .

Поэтому магнитный вектор Герца, возбуждаемый продольной щелью, имеет единственную компоненту ΠMz :

		V	d 2	l	πU ′
Μ			∫	∫cos			Μ	′ ′	(46)
Πx	=
		4πiωμd			2l	G33 du dv .
			−d 2 −l

27

В процессе интегрирования следует пользоваться методическими указаниями, изложенными в предыдущем подпункте. Искомые компоненты поля Η и Ε по – прежнему следует определять в соответствии с алгоритмом (3).

Запишем выражение для компонентыΗz вектора магнитного поля, возбужденного продольной щелью:

	V	∑εmεn cos	mπx		mπd			mπd
Ηz = −			0	sin						×
			a			2a		2a
	iωμab m,n

1

2

π

2

πz

2

×

k

−

cos

+ αmn

(π 2l )

2

2l

2l

mπx

mπy

×cos

cos

a

b

π cos γ				z		−iγ
			mn		e		l	×	(47)
							mn
2l		iγmn

Вопросы и упражнения

1.В чем заключается принципиальное различие выражений для полей, возбужденных щелью в области ее расположения и за ее пределами? Что можно сказать о характере типов волн, возбуждаемых симметрично расположенной поперечной щелью в широкой стенке прямоугольного волновода?

2.Пользуясь методическими указаниями, данными в настоящем разделе, получите

выражения (43) и (47) для полей Ηx и Ηz со всеми промежуточными выкладками.

3.Постройте алгоритм решения задачи возбуждения прямоугольного волновода продольной щелью в узкой стенке волновода.

СПИСОК ЛИТЕРАТУРЫ

1.Морс Ф.М.,Фешбах Г. Методы теоретической физики. Т.1. 1958. -930с., т.2. 1960. -886 с. М: Изд-во Иностр. лит.

2.Марков Г.Т., Панченко Б.А. Тензорные функции Грина прямоугольных волноводов и резонаторов. Изв. вузов Радиотехника, 1964, т.7, с.34-41.

3.Панченко Б. Тензорные функции Грина уравнений Максвелла для цилиндрических областей. Радиотехника. Республ. межвед. науч.-тех. сб., 1970, вып. 15, с. 82-91.

28

4.Y.Rahmat-Samii. On the Question of Computation of the Dyadic Green's Function for at the Source Region in Waveguides and Cavities. IEEE Trans. 1975, vol. MTT-3, N. 9, p. 762-765.

5.Chen –Tai, Powel Rozenfeld. Different Representations of Dyadic Green's Functionsfor a Rectangular Cavity. IEEE Trans. 1976, vol. MTT-4, N. 9, p. 597-601.

29