RF_5

7.4.Примеры решения задачи о колебании струны с различными граничными

иначальными условиями

Теперь конкретизируем задачу о колебании струны, конкретизировав функции f (x) и g(x) определенные значения.

ПРИМЕР 16. Найдем функцию u(x, t), описывающую

процесс колебания струны с закрепленными концами и начальными условиями

u(x, 0) = f (x),		∂u	(x, 0) = 0.	(38)
		∂t
Решение. Функция f (x)	задает начальное положение

струны, условие ∂u∂t (x, 0) = 0 говорит о том, что струна отпу-

щена без толчка. Эта модель описывает движение гитарной струны.

В соответствии с изложенным ранее, функция u(x, t) за-

дается формулой (35), в которой нам нужно найти коэффициенты an и bn так, чтобы выполнялись начальные условия

(38). Из условия

∂u

(x, 0) = 0 и формул (36) следует, что

bn = 0,

∂t

2

l

πnx

an =

Z0

f (x) sin

dx.

(39)

l

l

Поэтому

∞

u(x, t) =

an cos πnαt

sin πnx .

X

n=1

l

l

Используя формулу тригонометрии

sin α cos β =

1

(sin(α + β) + sin(α − β))

2

71

запишем решение в виде
1 ∞	πn	1 ∞	πn
u(x, t) = 2 n=1 an sin	l (x + αt) +	2 n=1 an sin	l (x − αt).
X		X
В силу (39) заключаем, что первая сумма представляет
собой разложение в	тригонометрический ряд функции
f (x + αt), а вторая функции f (x − αt).
Значит
u(x, t) =	1
	2 [f (x + αt) + f (x − αt)] .
Эту формулу называют формулой Даламбера. Она позволя-
ет представить решение в виде полусуммы ¾волны, бегущей
влево¿ f (x + αt) и ¾волны, бегущей вправо¿ f (x − αt).
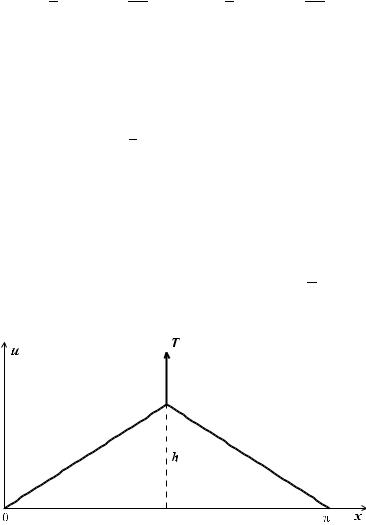
ПРИМЕР 17. Найдем функцию u(x, t), описывающую про-
цесс колебания струны, закрепленной на концах x = 0, x = π
и возбуждаемой оттягиванием ее в точке x =			π на величи-
			2
ну h (рис. 37). Начальная скорость равна нулю.
Рис. 37. Начальное положение струны из примера 17

72

Решение. Функция f (x) описывающая начальное поло-

жение струны задается формулой

	π x,			если 0 ≤ x ≤ 2			,
		2h				π
f (x) =
		2h		π
		π (π − x),		если 2	< x ≤ π.

Второе начальное условие имеет вид:

∂u

∂t

(x, 0) = 0.

Положения точек струны u(x, t) задаются уравнением (35). Подберем коэффициенты an и bn так, чтобы выполнялись

начальные условия

π	π	π
	2

2

Z

2 2h

Z

Z

0

0

2

an =

π

f (x) sin nx =

π

π

x sin nx +

(π − x) sin nx

=

π

8h sin

nπ

=

2

,

n2π2

2

π

∂u

bn =

Z0

(x, 0) sin nx = 0.

πnα

∂t

Итак, положения точек струны в момент времени t зада-

ются соотношением:

∞ 8h sin			nπ
X		2
u(x, t) =	n2	π2			cos nαt sin nx.
n=1
73

ЗАДАЧА

39. Найти функцию u(x, t), определяющую процесс колебания струны, закрепленной на концах x = 0, x = l, и возбуждаемой ударом молоточка ширины 2δ в точке струны с постоянной скоростью v0. Эта задача описывает колебания

струны рояля.

∞

Ответ

4v0l

1

πnc

πnδ

πnx

39. u(x, t) =

X

sin

sin

sin

sin ωnt,

2

α

2

l

π

n=1

n

l

l

где ωn =

l

, α = r

ρ

.

πnα

T

74

Список литературы

1.Александров В. А. Ряды Фурье: Метод. пособие. Ново-

сибирск: НГУ, 1996.

2.Ландау Л. Д., Китайгородский А. И. Физика для всех.

М.: Наука, 1974.

3.Тихонов А. Н., Самарский А. А. Уравнения математи-

ческой физики. М.: Изд-во МГУ, 1999.

75

Содержание

1. Разложение 2π-периодической функции в ряд

Фурье . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2. Разложение функции, заданной в промежут-

ке [0, π], только по синусам или только косинусам 24

3. Ряд Фурье функции с произвольным периодом . . . . 33 4. Комплексная форма ряда Фурье . . . . . . . . . . . . . . . . . . . 40 5. Равенство Ляпунова . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 6. Дифференцирование рядов Фурье . . . . . . . . . . . . . . . . . 51 7. Применение рядов Фурье для решения дифферен-

циальных уравнений в частных производных . . . . 57 7.1. Вывод уравнения свободных малых поперечных

колебаний струны . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 7.2. Решение уравнения свободных малых поперечных

колебаний струны методом Фурье . . . . . . . . . . . . . . . . 62 7.3. Сила, высота и тембр звука . . . . . . . . . . . . . . . . . . . . . . 69 7.4. Примеры решения задачи о колебании струны с

различными граничными и начальными условиями . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71 Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .75

76