Метода термодинамика(лекции)

Здесь через const обозначены параметры, не зависящие от значения εi и

свойств подсистемы. Формула определяет вероятность того, что слабо взаимодействующая часть некоторого собрания произвольных физических

систем будет находиться в одном из Ω(εi ) состояний с энергией между εi и

εi + δεi , а термостат – в одном из состояний с энергией между E −εi и

E −(εi + δεi ). Но так как состояние термостата не представляет интереса,

для краткости говорят, что w(εi ) – вероятность нахождения подсистемы в одном из состояний с энергией εi . Из определения вероятности следует условие нормировки

∑w(εi ) = 1,	(1.57а)
i

где суммирование ведется по всем возможным квантовым состояниям системы. Отсюда вытекает, что введенный формально коэффициент θ является существенно положительной величиной:

	∂E	> 0 .	(1.57б)
θ =
	∂σ ε =0
	i

Только в этом случае вероятность состояний сколь угодно больших энергий стремится к нулю. Постоянная в (1.56) находится из условия нормировки

const = 1 ∑e−εi 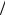θΩ(εi ),

и распределение вероятностей принимает вид

wi	=	e−εi θΩ(ε )		(1.58)
		∑e−εi	θΩ(εi ) .
			i

Оно впервые предложено Дж. Гиббсом (1901 г) для классических систем и получило название распределение Гиббса или канонического распределения.

Сумма, стоящая в знаменателе, играет большую роль в статистической физике, для нее введено специальное обозначение

Z = ∑e−εi θΩ(εi ),

(1.59)

52

и принято называть функцией (интегралом) состояния (статистической суммой). Распределение Гиббса позволяет вычислить среднее значение любой физической величины L(εi ), зависящей от состояния системы:

			= ∑L(εi )w(εi ) =	1	∑L(εi )e−εi θΩ(εi ).	(1.60)
	L
				Z

1.6.3. Квазиклассическое приближение . Переход от квантового описания системы к квазиклассическосму проведем следующим образом. Внутренняя энергия макроскопических систем меняется непрерывно, и квантовые эффекты не имеют существенного значения (см. раздел 1.3 и формулу (1.35) при a → ∞). Из распределения Гиббса следует, что для замены ступенчатой функции e−εi θ плавной – e−εθ необходимо, чтобы интервалы между энергиями ∆εi = εi+1 −εi были малы по сравнению с θ. Это означает, что переход к квазиклассической статистике должен происходить при прочих равных условиях в области высоких температур θ >> ∆εi .

Состояние системы, состоящей из N частиц и имеющей 3N степеней свободы, в квазиклассическом приближении определяется значениями координат (qi ) и импульсов ( pi ). Ее энергия является непрерывной функцией всех координат и импульсов ε(p,q). Это позволяет говорить о непрерывном распределении вероятностей того, что система находится в одном из состояний в интервале энергий между ε(p,q) и ε(p,q) + δε(p,q). Учитывая, что согласно

(1.40), число таких состояний равно Ω(ε)dε = (1 h3N ) (dΓ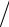dε)dε,

распределение Гиббса в квазиклассическом приближении принимает вид

	dw =		e−ε(p,q) θ				∂Γdε,		(1.61)
			Z h3N
							∂ε
	где
	Z =	1		∫e−	ε(p,q)			∂Γdε	(1.62)
					θ
		3N
		h						∂ε

53

Отличие этой формулы от (1.59) состоит в том, что сумма по состояниям заменена интегралом. Интегрирование ведется по всему фазовому пространству, доступному для системы, т.е. по всем дозволенным значениям координат и импульсов системы.

1.7. Свойства распределения Гиббса

Область применения распределения Гиббса ограничена следующими условиями:

1)система находится в равновесном состоянии;

2)наличие макроскопической системы (термостата), составляющей ее окружение (термостата);

3)слабое взаимодействие между системой и термостатом.

Востальном свойства системы произвольны, в частности, не зависят от характера взаимодействия и ее агрегатного состояния.

Поскольку статистическая температура θ положительная величина (1.57б), то энтропия, а, следовательно, и число состояний (σ = ln Ω) являются монотонно возрастающей функцией энергии. Чем больше частиц содержит

система, тем больше состояний Ω(εi ) , отвечает данному значению интервала энергии (εi, εi +δεi ). С ростом энергии (увеличением квантового числа n )

резко возрастает плотность энергетических уровней (1.35б). Поэтому рост

Ω(εi ) с энергией происходит тем быстрее, чем больше частиц в системе.

Чтобы выяснить характер зависимости распределения Гиббса w(ε) от энергии, необходимо вычислить производную ∂Γ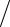∂ε (1.61). Расчеты

проведем для ансамбля молекул идеального газа. Объем части фазового пространства, в котором энергия газа не превышает ε, по определению, равен интегралу

Γ = ∫dp1...dp3Ndq1...dq3N ,

54

где пределы интегрирования следуют из условия

3N

∑pi2 2m ≤ ε(p,q). (1.63)

i=1

Оно не включает координаты молекул, по которым можно интегрировать непосредственно

Γ =V N ∫dp1...dp3N ,

(1.64)

поскольку для каждой молекулы можно написать

V= ∫dq1dq2dq3 .

Сгеометрической точки зрения формула (1.63) определяет в импульсном

пространстве 3N измерений шар, радиус которого равен R = 2mε , а

интеграл в (1.64) представляет его объем. В трехмерном пространстве объем пропорционален R3 , т.е. ~ ε3/2 . Исходя из соображений размерности в 3N –

мерном пространстве он пропорционален R3N . Поэтому из (1.64) следует

Γ = const R3N V N = const ε3N /2 V N .

После дифференцирования имеем

∂Γ	= const ε	(3N /2)−1	V	N	(1.65)
∂ε

Постоянная не имеет особого значения, поскольку оно будет сокращаться с такой же постоянной, возникающей при вычислении Z . Поэтому распределение Гиббса принимает вид

dw = const	e−	ε	3N	−1 V Ndε.
		θ	ε 2
h3N Z

3N	−1	3N
Поскольку множитель ε 2		ε 2

весьма быстро растет с увеличением ε, а

множитель e−θε , напротив, резко убывает, функция распределения Гиббса для макроскопических систем (N ≈ 1023 моль-1) имеет очень резкий максимум, степень его размытости совершенно ничтожна. Это означает, что вероятность нахождения системы в состояниях с энергией, заметно отличающейся от

55

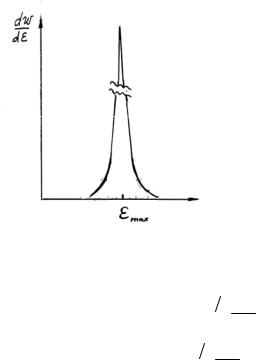
энергии εmax , отвечающей максимуму распределения Гиббса, практически равна нулю (рис. 1.5). Такой характер зависимости позволяет в первом приближении отождествить ее с δ(εmax −ε)–дельта функцией Дирака,

которая определяется для непрерывной функции ϕ(x) при ϕ(x → ±∞) → 0

		операторным соотношением
	dw
	dε	∞
		∫ ϕ(x)δ(x −a)dx = ϕ(a).
		−∞

			В макросистемах εmax практически совпадает
			со средним значением энергии ε . Поэтому
			средняя величина какого-либо физического
	εmax	ε	параметра L(ε) макроскопической системы
Рис. 1.5.			есть функция средней энергии

			∫ L(ε)e	−ε θ ∂Γ
		=			∂ε dε	=	∫ L(ε)δ(εmax −ε)dε		= L(ε) .	(1.67)
	L(ε )
	i				∂Γdε		∫ δ(εmax −ε)dε
			∫e−ε θ
					∂ε
По сути это означает, что состояние с энергией								ε = ε осуществляется с
полной достоверностью,					а при		остальных	энергиях невозможно
w(ε ≠ ε) = 0 .

1.8. Большое каноническое распределение Гиббса

Взаимодействие подсистемы с окружением в общем случае осуществляется взаимным обменом не только энергией, но и частицами. В процессе взаимодействия частицы уходят из подсистемы или приходят в нее, унося или принося при этом соответствующее количество энергии. Обмен энергией и частицами происходит одновременно. В такой ситуации переменной является не только энергия, но и число частиц в ней. При этом

56

выделенная подсистема может побывать во всех квантовых состояниях, отличающихся числом частиц.

Примером систем с переменным числом частиц могут быть капля или кристалл (лед), находящийся в равновесии с паром или расплавом (водой), соответственно. Последние играют роль окружения (термостата). Молекулы с поверхности жидкости переходят в пар, а молекулы из пара конденсируются на поверхности жидкости. Тоже происходит с молекулами на поверхности кристалла. Если систематического перехода частиц из пара в жидкость или обратно не происходит, то в системе установится состояние равновесия, при котором число частиц, переходящих в обоих направлениях, уравнивается. Подобная ситуация имеет место и в равновесной химической реакции. В выделенной подсистеме (например, молекулах соединения AB ) число частиц изменяется: уменьшается за счет реакции распада AB → A +B и увеличивается за счет синтеза A +B → AB .

Для характеристики состояния таких систем необходимо указать не только ее полную энергию, но и число частиц, которое в ней содержится.

Задача заключается в нахождении распределения вероятностей win того, что подсистема находится в i -ом состоянии и содержит при этом n частиц. Ее решение проведем по алгоритму, изложенному в разделе 1.6.2. Отличие состоит в том, что число состояний системы с данной энергией Ω(εi ) следует заменить на Ω(εi,n) , где учитывается число частиц, а число состояний термостата – на Ω0(E0,N0 ) . Поскольку сумма числа частиц в подсистеме и термостате остается постоянной N = n +N0 = const , вместо формул (1.51)

и (1.53) получаем

win ~ Ω0(E −εi,N −n) Ω(εi				,n),
					(1.68)
Ω0(E −	εi,N −n) e	σ(E−εi	,N −n)		.

Так как размеры термостата, его энергия и число содержащихся в нем частиц велики, то для всей замкнутой системы (подсистема + термостат) справедливы

57

неравенства εi << E и

n << N . Поэтому,

как и в разделе 1.6.2, можно

разложить функцию σ в ряд по степеням εi

и n и ограничиться линейными

членами разложения

∂σ

∂σ

n +....

σ(E −ε,N −n)

σ(E,N) −

ε

−

i

i

∂E ε =0

∂N n=0

i

И для вероятности имеем

w

= const e

−

εi −µn

Ω(ε,n).

(1.69)

in

θ

i

Статистическая температура по-прежнему вычисляется по формуле (1.55)

θ = (∂E ∂σ)	. Коэффициент µ называется				химическим (парциальным)
ε =0
	i
потенциалом и определяется выражением
		∂σ		,	(1.70)
	µ = −θ
		∂N n=0

где производная берется при постоянном значении энергии и внешних

параметров. Из условия нормировки		∑∑win				= 1 находится постоянная
			i n
величина
			µn−εi			−1
				Ω(εi
			θ
const = ∑∑e					,n) .
	i n

Искомое распределение вероятностей состояний системы с переменным числом частиц принимает вид

win	=	e−(εi −µn) θΩ(ε,n)		1			−(ε −µn) θ	Ω(εi	,n).	(1.71)
		∑∑e−(εi	−µn) θΩ(εi,n)	= Z e			i
			i

i n

Здесь через Z обозначена функция состояний, которая при постоянном числе частиц в системе n = n совпадает с (1.60). Полученная формула называется

большим каноническим распределением Гиббса. Оно позволяет находить

58

средние значения любой величины L(εi,n), зависящей от состояния системы и числа частиц:

L = 1 ∑∑L(εi,n)e−(εi −µn)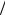

Z i n

θΩ(εi,n) . (1.72)

В частности, среднее число частиц при произвольном значении энергии системы равно

			=	1	∑∑ne−(εi −µn) θΩ(εi,n) = θ	∂	ln ∑∑e−(εi −µn) θΩ(εi,n) = θ	∂	ln Z .
		n
						∂µ		∂µ
				Z i n			i n

(1.73)

Это по существу первый и далеко не единственный пример определения физических параметров через функцию состояний.

Рассмотрим равновесную систему, состоящую из двух подсистем, также находящихся в состоянии статистического равновесия и слабо взаимодействующие между собой (обмениваются частицами и энергией). Для каждой из них можно записать

w	1	= Ae(µ1n1 −εi1 ) θ1	Ω ,	w	2	= Ae(µ2n2 −εk 2 ) θ2	Ω .
		1	1			2	2

Поскольку подсистемы слабо взаимодействуют, то, согласно теореме умножения вероятностей, для вероятности одновременного нахождения первой системы в i -ом, а второй – в k -ом состояниях находим

w′	= w w	2	= Ae(µ1n1 −εi1 ) θ1	Ae(µ2n2 −εk 2 ) θ2	Ω Ω .
12	1		1	2	1	2

Две подсистемы образуют одну равновесную систему с суммарной энергией

(εi1 + εk 2 ) и числом частиц (n1 +n2 ), для которой также справедливо большое каноническое распределение

′′	= Ae	µ(n +n )−(ε	+ε )	θ	Ω.
w12		1 2 i1	k 2

Если подсистемы находятся в состоянии равновесия, то при установлении взаимодействия между ними их состояние не должно изменяться. Поэтому необходимо, чтобы вероятности w12′ и w12′′, определенные последними двумя

59

равенствами, были тождественно равны друг другу w′	≡ w′′	. Отсюда
12	12
следуют равенства
θ = θ1 = θ2 , µ = µ1 = µ2 .		(1.74)

С физической точки зрения, это означает равенство температур и парциальных потенциалов во всех квазинезависимых подсистемах, входящих в состав равновесной системы. Согласно молекулярным представлениям, равенство температур выражает требование, чтобы количества энергии, отдаваемое и получаемое подсистемой, были равны друг другу. В равновесном состоянии при обмене частицами не только совпадает числа приходящих и уходящих из подсистемы частиц, но равны и средние энергии, переносимые этими частицами – об этом свидетельствует равенство парциальных потенциалов. Если бы это было не так, например, уходили только быстрые, а приходили только медленные частицы, то состояние равновесия было бы нарушено.

Статистические температура θ и парциальный потенциал µ определяют состояние термостата. Только в том случае, когда выделенная подсистема является макроскопической, условия равновесия позволяют относить θ и µ к

самой подсистеме. Не имеет смысла говорить о температуре и парциальном потенциале микроскопической подсистемы, например, молекулы.

Вквазиклассическом приближении число состояний системы Ω(εi,n) , как

ив разделе 1.6.3, можно выразить через объем фазового пространства ∆Γn

Ω(ε,n) = ∆Γ	n	h3n .	(1.74)
i

Здесь величина объема фазового пространства в отличие от систем с постоянным числом частиц изменяется с изменением числа частиц (степеней свободы 3n )

∆Γn = ∆q1∆q2...∆q3n ∆p1∆p2...∆p3n .

И большое каноническое распределение принимает вид

dwin	=	1		e−(ε−µn) θdΓn ,	(1.75)
			3n
		Z h

60

где функция состояния выражается следующим образом

Z = ∑∫e−(ε−µn)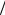θdΓn .

n

Приведенные положения статистической физики и распределения в равновесных системах относятся к широкому классу веществ. Конкретизации найденных закономерностей посвящены следующие разделы книги, где будут рассмотрены различные физические системы с учетом характера движения молекул, квазичастиц, типов взаимодействия. Общность законов статистической физики позволила не ограничивать круг ее рассмотрения чисто тепловыми процессами, но включить в нее самые разнообразные макроскопические свойства тел – оптические, электрические, магнитные, химические и т.п.

61