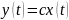- •Тема 1. Теория сигналов.
- •Спектры гармонических сигналов
- •Спектры непериодических сигналов
- •Свойства преобразования ф.
- •Тема 2. Вероятностные методы теории информационных процессов.
- •Моментные функции случайных процессов
- •Свойства корреляционных функций
- •Эффективный интервал корреляции
- •Взаимные моменты случайных процессов
Моментные функции случайных процессов
Математическое ожидание случайного сигнала (по сечению)
Непрерывный сигнал:
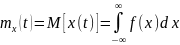
Дискретный по амплитуде (квантованный) сигнал:
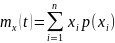
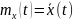
Начальные моменты k-го порядка:
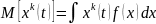
Центральные моменты k-го порядка:
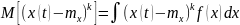
Центральный момент 2-го порядка – дисперсия:
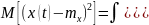
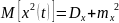
Для описания/моделирования временной взаимосвязи сечений случайного процесса используется:
корреляционная функция:
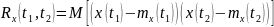
Ковариационная функция
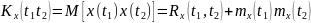
При
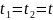
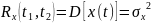
Нормирование корреляционной и ковариационной функции:
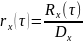
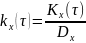
Свойства:
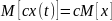
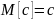
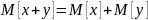
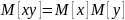
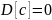
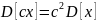
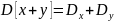
Допущения и упрощения при моделировании случайных процессов:
Стационарность:
В широком смысле:
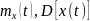 и
и
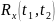 – инвариантны относительно сдвига во
времени:
– инвариантны относительно сдвига во
времени:
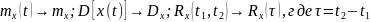
В узком смысле:
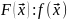 - инвариантны относительно сдвига во
времени.
- инвариантны относительно сдвига во
времени.
Эргодичность:
Моментные функции, полученные для сечений с вероятностью, стремящейся к 1, совпадают со средними значениями, полученными на оной реализации по времени наблюдения
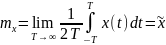

Для
характеристики стационарных в широком
смысле случайных процессов в частотной
области используется
 – спектральная плотность стационарного
случайного процесса – преобразования
Ф от корреляционной функции (в комплексной
форме):
– спектральная плотность стационарного
случайного процесса – преобразования
Ф от корреляционной функции (в комплексной
форме):

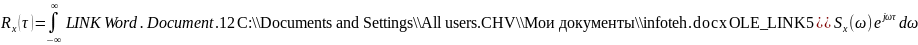
Физический
смысл
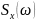 -
разложение средней мощности случайного
сигнала по частотам.
-
разложение средней мощности случайного
сигнала по частотам.
Действительная форма спектрального разложения:
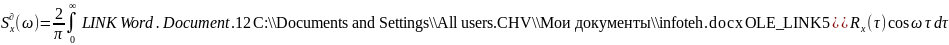
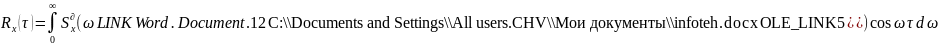
При
этом
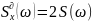 при
при
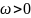
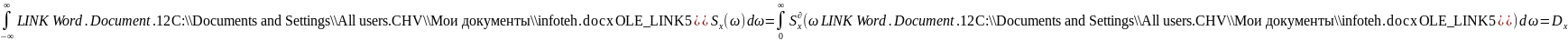
Свойства корреляционных функций
Для стационарных процессов:
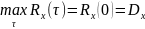 или
или
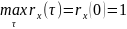
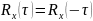
Для эргодических процессов:
Эффективный интервал корреляции
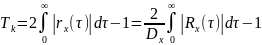
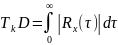
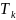
 –
неслучайная
функция,
–
неслучайная
функция,
то
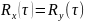 не изменится.
не изменится.
т.к.
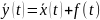 ,
то
,
то
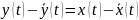 и т.д.
и т.д.
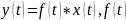 -
неслучайная функция,
-
неслучайная функция,
то
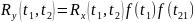
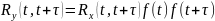

Взаимные моменты случайных процессов
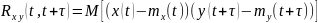
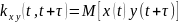
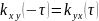
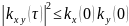
Произвольная функция, не обладает свойством четности или нечетности.
Если
один из процессов центрированный, то
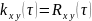
Коэффициент корреляции двух процессов характеризует степень линейной зависимости процессов при сдвиге τ:
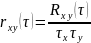
Статистическая
зависимость
для двух случайных величин: мера их
линейной статистической связи –
коэффициент корреляции
 :
:
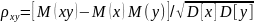

В
частном случае, если
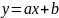 ,
то
,
то
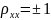 .
.
При
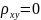 случайная величина некоррел., т.е.
случайная величина некоррел., т.е.
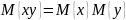
Линейные преобразования случайных функций.
Если
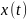 c
c
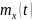 и
и
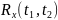 преобразуется однород. линейным
оператором
преобразуется однород. линейным
оператором
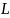 в случайную функцию
в случайную функцию
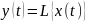 ,
то
,
то
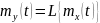
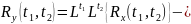
Однородное линейное преобразование применить дважды, сначала по одному аргументу, затем по другому.
Сложение случайных функций:
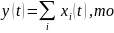
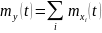
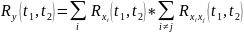
Умножение на неслучайную функцию
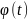 :
:
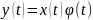
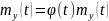
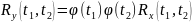
Стационарная линейная система с частотной характеристикой
 :
:

Если
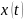 – детерминированная функция, то
– детерминированная функция, то
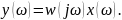
Если
– случайная функция, то
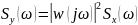
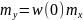
New Version
Эффективный интервал корреляции
Нормирование случайных процессов и корр. функции.
Нормированная случайная функция:
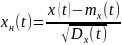
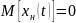
Центрированная
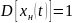
Нормированая корр. функция:
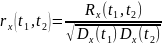
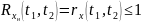
Эффективный интервал корр.:
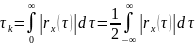
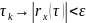
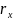
Эффективная ширина спектра
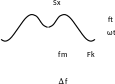
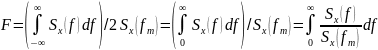
Аналогично
для
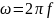 .
.
Взаимные моменты случайных процессов
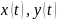 – например,
вход-выход
– например,
вход-выход
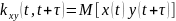
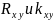 в целом не обладают
свойствами четности или нечетности, но
в целом не обладают
свойствами четности или нечетности, но
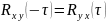 ,
если один процесс центрированный, то
,
если один процесс центрированный, то
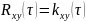
Статистическая зависимость случайных величин
Мера линейной статистической связи - коэффициент корреляции:
Пример:
при
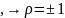 .
.
При
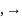 случайная величина
случайная величина
 ,
т.е.
,
т.е.
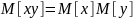
Каноническое разложение случайных процессов
Понятие простейшей случайной функции:
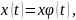
– детерминированная функция
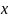 – случайная
величина.
– случайная
величина.
Тогда
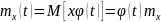
Если
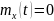 ,
то
– элементарная случайная функция. Для
нее
,
то
– элементарная случайная функция. Для
нее

Любую
центрированную случайную функцию
 можно представить в виде взаимно
некоррелируемых случайных элементарных
функций
можно представить в виде взаимно
некоррелируемых случайных элементарных
функций
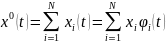
Из
взаимной некорр.
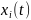 следует некоррелируемость
.
следует некоррелируемость
.
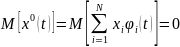
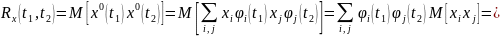
В
силу взаимной некорр.
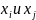 остается один член при
остается один член при
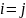 ,
равный
,
равный
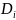
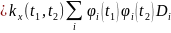
Произвольная нецентрир. случайная функция:
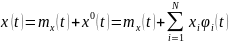
Это и есть каноническое разложение.
- коэффициент разложения,
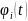 -
координатные функции.
-
координатные функции.
При
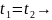

Таким образом, зная каноническое разложение , можно сразу получить каноническое разложение ее корр. функции, и наоборот.
Преобразование случайных процессов

Линейная система
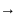 ее реакция на
входные сигналы
ее реакция на
входные сигналы
Аддитивная (принципы суперпозиции)
Однородная (принципы пропорционального подобия)
Аддитивность:
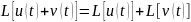
Однородность:
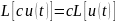
Примеры
Умножение на заданную функцию:
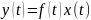
Дифференцирование:
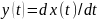
Интегрирование:
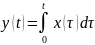
Если c и преобразуется однород. линейным оператором в случайную функцию , то
Однородное линейное преобразование применить дважды, сначала по одному аргументу, затем по другому.
Сложение случайных функций:
Умножение на неслучайную функцию :
Частотное представление:

Связка:
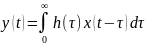
Для реализации:
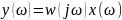
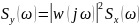
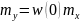
Функция преобразования случайных величин с точки зрения функции распределения вероятности
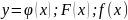
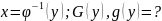
Область монотонности:

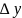
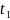
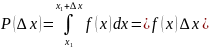
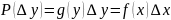

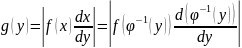
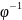 – обратная функция.
– обратная функция.
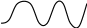
Примеры:
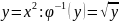
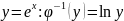
Математические модели искажения сигнала шумом
Аддитивный шум

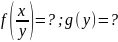
Сигналы
и шум независимы. Исходим, что
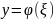 при заданном значении
.
Т.е., например,
при заданном значении
.
Т.е., например,
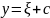 ,
,
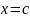 .
.
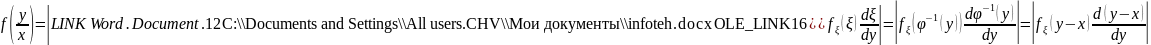
Т.к.
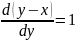
То:
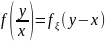
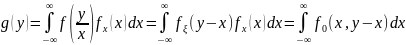
В
общем виде для зависимых
и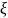 :
:
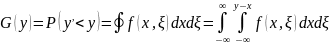
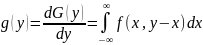

Многомерный случай

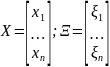
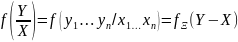
Пусть
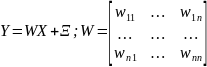

Мультипликативный шум
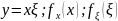
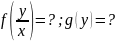
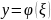 при заданном
значении
при заданном
значении
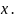
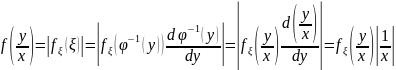
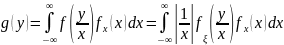
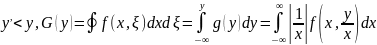


Влияние шума (искажения) при передаче квантованных (дискретных по значению) сигналов

Наиболее общая
характеристика (модель) – матрица
вероятностей совместного появления
сигналов
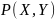
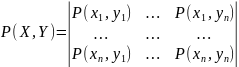
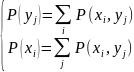
Формула Байеса:
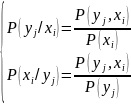
Специальные (типовые) виды (модели) случайных сигналов
Белый шум (аналог белого света = ∑ всех спектральных составляющих, имеющих одну интенсивность). Белый шум = ∑ гармонических колебаний всех частот, имеющих одну и ту же дисперсию амплитуды.
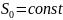 – ст. белый шум
– ст. белый шум
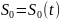 – нест. белый шум
– нест. белый шум
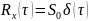
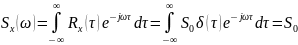
Приближенный аналог белого шума:
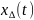 – дискретный белый
шум. Значения
на
различных интервалах
– дискретный белый
шум. Значения
на
различных интервалах
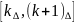 - независимы.
- независимы.

Обозначим
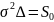 ,
если
,
если
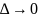 и при этом
и при этом
 возрастает
так, чтобы
,
то
возрастает
так, чтобы
,
то
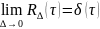
Ограниченный по полосе белый шум
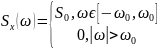
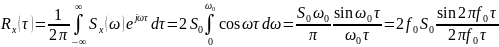
RC-шум - результат прохождения белого шума через RC-цепь (апериодическое звено)

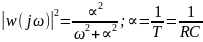
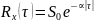
Гауссовский шум – результат ∑ статически независимых белых шумов:
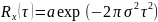
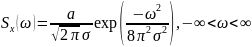
Эффективный
интервал корреляции
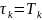 :
:
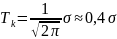
Эффективная ширина спектра:
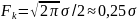

Гауссовские случайные сигналы (процессы) –
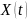
Для
любого набора
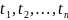 все
распределения вероятностей подчиняются
нормальному закону, в том числе
многомерные.
все
распределения вероятностей подчиняются
нормальному закону, в том числе
многомерные.
Композиция гауссовских процессов порождает гауссовский процесс. Плотность вероятности любых сечений :
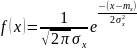
Гауссовский
процесс однозначно определяется
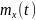 и
и
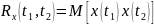
Многомерное нормальное распределение:
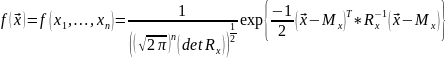
Где
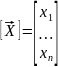 ;
;
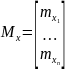 ;
;
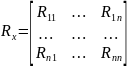
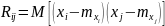
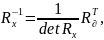
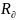 – матрица
алгебраических дополнений.
– матрица
алгебраических дополнений.
Частный
случай – случай независимых отсчетов.
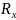 ,
следовательно, преобразуется в
диагональную матрицу:
,
следовательно, преобразуется в
диагональную матрицу:
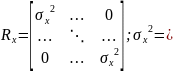

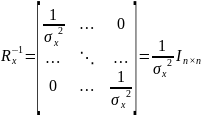
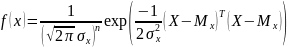
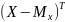 -
строка,
-
строка,
 –
столбец.
–
столбец.
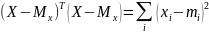
Для
стационарных и эргодических процессов
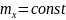 .
.
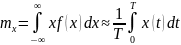
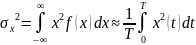
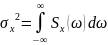
Следовательно, для любого нормального процесса его любая характеристика может быть определена по и
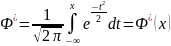
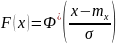
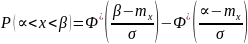
Нормальный случайный процесс полностью определяется своим математическим ожиданием и корреляционной функцией, которые могут быть вычислены по двумерной функции распределения.
Для случайного процесса с независимыми значениями (отсчетами) достаточно задания одномерного закона распределения.
Любое линейное преобразование нормального процесса распределено нормально.
Случайный телеграфный сигнал.
Случайный
телеграфный сигнал
– это сигнал
,
который меняет свои значения в случайные
и независимые моменты времени, а внутри
интервалов времени сохраняет значения
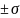 .
.
Случайный
параметр – значение
переменного знака сигнала за интервал
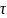 .
Этот параметр распределен по закону
Пуассона:
.
Этот параметр распределен по закону
Пуассона:

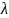 – интенсивность
переключений.
– интенсивность
переключений.
Моменты переключений не зависят от текущего и будущего поведения процесса. Вероятность того, что не произойдет ни одного изменения состояния:
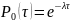
Вероятность того, что изменение произойдет хотя бы один раз:

Интервал времени между последовательными изменениями есть случайная величина с плотностью распределения и математическим ожиданием соответственно:
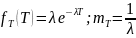
Для телеграфного сигнала (он полностью определен процессом Пуассона) и при этом стационарен и эргодичен:

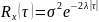
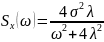
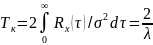
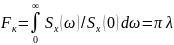
Вывод:
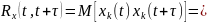
Произведение
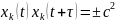 в зависимости от совпадения знаков.
в зависимости от совпадения знаков.
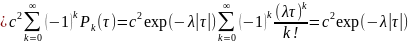
Синусоидальный случайный процесс:
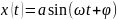
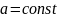 ,
,
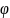 – случ. и равно-распр. на
– случ. и равно-распр. на
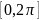
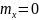 ,
,
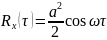
Процесс стационарен и эргодичен.
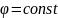 ,
,
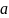 - случайная величина с
- случайная величина с
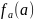
,
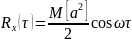
Процесс стационарен, но в целом не эргодичен.
Марковские сигналы (процессы без последействия)
Введем
обозначение:
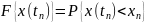 .
Дискретный или непрерывный случайный
процесс
называется Марковским, если для любого
набора
.
Дискретный или непрерывный случайный
процесс
называется Марковским, если для любого
набора
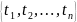 .
.
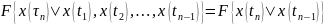
т.е.
если для
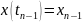 ,
то значение
,
то значение
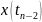 ничего не добавляет (никакой информации)
для определения распределения
ничего не добавляет (никакой информации)
для определения распределения
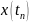 .
Т.е. Марковский процесс определяется
своим распределением вероятности
второго порядка и, следовательно, может
быть задан распределением вероятности
первого порядка + вероятностями перехода.
.
Т.е. Марковский процесс определяется
своим распределением вероятности
второго порядка и, следовательно, может
быть задан распределением вероятности
первого порядка + вероятностями перехода.
Дискретный Марковский процесс с дискретным временем называют цепью Маркова. Цепь Маркова имеет вид:
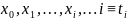
– случайная
величина, принимающая значения из
множества
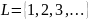
Марковские цепи есть модель схемы независимых испытаний, когда существует зависимость исхода любого состояния только от исхода предыдущего.
Имеем
систему с дискретными состояниями. Если
система в момент времени
(т.е.
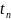 )
находилась в состоянии
)
находилась в состоянии
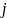 ,
то вероятность перехода в состояние
в момент
,
то вероятность перехода в состояние
в момент
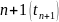 зависит в общем случае от
зависит в общем случае от
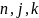 и не зависит от того, в каких состояниях
система находилась в момент времени до
и не зависит от того, в каких состояниях
система находилась в момент времени до
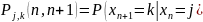
Следовательно, цепь Маркова определяется через условные вероятности того, что система осуществит длинный переход.
Цепь Маркова называется однородной, если переходные вероятности не зависят от времени, т.е.
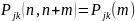
Обозначим
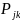 - вероятность
перехода за один шаг. Тогда цепь Маркова
будет описываться матрицей переходных
вероятностей:
- вероятность
перехода за один шаг. Тогда цепь Маркова
будет описываться матрицей переходных
вероятностей:
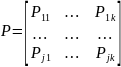
Матрица квадратная, неотрицательная, ∑ вероятностей по любой строке =1.
Многошаговые переходные вероятности.
Необходимо определить вероятность перехода системы из состояния в состояние за шагов. Цепь однородна.
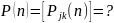
Оказывается,
что для нахождения
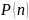 достаточно знать матрицу одношаговых
переходов
достаточно знать матрицу одношаговых
переходов
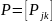 .
Покажем это.
.
Покажем это.
Вводим
промежуточный момент (шаг)
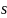 :
:
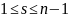 и будем рассматривать переход из
в
в два этапа:
и будем рассматривать переход из
в
в два этапа:
в
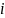 за
шагов,
за
шагов,
в за ) шагов.
Тогда из формулы полной вероятности:
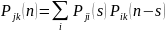
Следовательно
элемент матрицы, полученный как
произведение
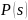 и
и
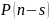 ,
т.е.
,
т.е.
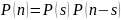 - уравнение
Колмогорова-Чепмена.
- уравнение
Колмогорова-Чепмена.
Т. матрица переходных вероятностей за шагов и ) шагов.
Пусть
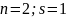 ,
то:
,
то:
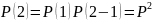
Если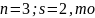 :
:
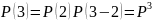 и т.д.
и т.д.
т.е.:
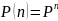
Если представить исходное распределение вероятностей состояний системы в виде матрицы-строки:
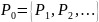 ,
,
то вероятности состояний системы в момент времени :
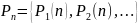
Можно получить из уравнения:
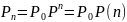
Марковские модели содержат полную информацию о двумерном законе распределения.
Пример Марковского процесса:

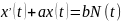
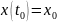
Марковский процесс 2-го порядка:

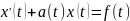
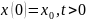
Зафиксируем
,
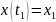 .
Решение определяется уравнением:
.
Решение определяется уравнением:
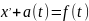 ,
,

Т.е.
от прошлого
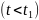 не зависит. Для линейных операторов
второго порядка – нет, для определения
состояния при
не зависит. Для линейных операторов
второго порядка – нет, для определения
состояния при
 необходимо знать не только
необходимо знать не только
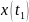 ,
но и, например,
,
но и, например,
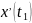 .
.
Классификация состояний
Смежные состояния – возможен переход за один шаг. Граф состояния системы:
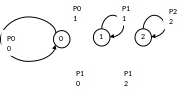
Вершины графа на рисунке – это состояния (все – вершины на шаге ), дуги – направление и вероятность перехода между смежными состояниями.
Для построения графа Марковской цепи удобно использовать матрицу смежности.
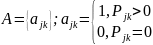
Состояние
достигнуто из состояния
,
если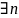 такое, что
такое, что
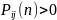 .
.
Пользуясь
графовым представлением Марковского
процесса, легко определить множества
состояний, достижимых из фиксированного
состояния
.
Для этого нужно найти матрицу достижимости
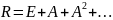 ,
где
,
где
 - единичная матрица,
- матрица смежности.
- единичная матрица,
- матрица смежности.
Состояния
и
называются сообщающимися,
если
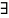 такое
и
такое
и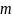 ,
что
,
что
 .
Состояние
называют несущественным,
если
такое состояние
.
Состояние
называют несущественным,
если
такое состояние
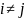 ,
которое достижимо из
,
но состояние
недостижимо из
.
,
которое достижимо из
,
но состояние
недостижимо из
.

Все существующие состояния цепи естественно разбиваются на классы так, что все состояния принадлежащие одному классу, сообщаются, а разным классам – не сообщаются.
Цепь Маркова называется неприводимой, если существует (ей соответствует) единственный класс сообщающихся состояний.
Подмножество С состояний цепи Маркова называют замкнутым если никакое состояние вне С не может быть достигнуто ни из какого состояния, входящего в С.

Отражающий экран:

Поглощающий экран:

Эргодические цепи Маркова.
При
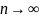
 становится независимой от состояний
и стремится к предельной вероятности:
становится независимой от состояний
и стремится к предельной вероятности:
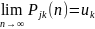
Распределение
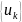 называется стационарным распределением
вероятностей эргодической цепи Маркова,
т.е.
называется стационарным распределением
вероятностей эргодической цепи Маркова,
т.е.
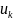 - вероятность того, что система будет
находиться в состоянии
при
- вероятность того, что система будет
находиться в состоянии
при
 .
При этом:
.
При этом:
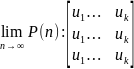
Алгоритм нахождений - решение системы линейных уравнений:
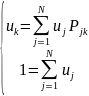
Дискретный Марковский процесс с непрерывным временем.
- случайный процесс с дискретным множеством состояний (конечным) и непрерывным временным параметром.

Переключения могут происходить в любой момент времени. Моменты переключений заранее не известны и их совокупность - случайный поток событий (управляющий поток событий).
Поскольку мы рассматриваем процесс без последствия (т.е. М.), то характеристики потока (с управлением) не могут быть любыми.
Марковское свойство:
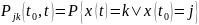
 не зависит от того,
как протекает процесс до
не зависит от того,
как протекает процесс до
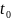 ,
в частности, как долго до
процесс находился в состоянии
.
Оказывается, что единственным решением
данной задачи, является поток событий,
в котором интервалы времени между
соседними событиями распределены по
показательному закону. Такой поток
случайных событий называется Пуассоновским
потоком.
Для него
,
в частности, как долго до
процесс находился в состоянии
.
Оказывается, что единственным решением
данной задачи, является поток событий,
в котором интервалы времени между
соседними событиями распределены по
показательному закону. Такой поток
случайных событий называется Пуассоновским
потоком.
Для него
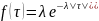
Распределение вероятностей
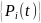 состояний дискретного
Марковского процесса с непрерывным
временем. Считаем, что с каждым состоянием
системы связан пуассоновский поток с
состояний дискретного
Марковского процесса с непрерывным
временем. Считаем, что с каждым состоянием
системы связан пуассоновский поток с
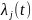 .
Обозначим
.
Обозначим
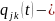 условная
вероятность перехода из
условная
вероятность перехода из
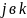 при условии появления события в
-м
управляющем потоке. Тогда, используя
формулу полной вероятности при
при условии появления события в
-м
управляющем потоке. Тогда, используя
формулу полной вероятности при
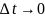 , получим для любого
:
, получим для любого
:

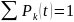
Или
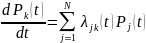

Получили уравнение Колмогорова. Ценность – обыкновенное дифференциальное уравнение первого порядка.