Лесотранспортная логистика. Решение задач

спрос на 14-й месяц, нужно дождаться получения фактических данных о 13-м месяце ит.д..

2.1.4. Метод скользящего среднего.

Прогнозные оценки определяются путем расчета среднего арифметического нескольких последних наблюдений.

y(m+1) =( ym+ym-1+ym-2+ ym-3+ym-4 )/5

(2.27)

2.2. ПРИМЕР ПРОГНОЗИРОВАНИЯ РАЗВИТИЯ МАТЕРИАЛЬНОГО ПОТОКА.

Исходные данные:

Спрос на продукцию лесопромышленного предприятия за предыдущие 12 месяцев составляет:

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
Спрос в
условных	180	198	209	208	220	250	210	220	223	240	210	260
единицах

Выполнить:

Установить план производства на первые три месяца следующего периода с вероятностью 0,98 и 0,95.

Прогнозирование выполнить методами наименьших квадратов, методом Чебышева. Оценить погрешность. Представить графики и дать выводы.

2.2.1. Прогнозирование развития методом наименьших квадратов.

Определение уравнения регрессии первого порядка.

Построив график изменения спроса за предыдущий период, делаем пред-

положение, что эмпирическая линия регрессии имеет вид линейной функции, которая представлена в виде: y=at+b, где a и b определяются по формулам:

	n
a =	∑(ti − mi )( yi − my )
	i=1						(2.28)
	n
	∑(ti − mi ) 2
	i=1
	b = my − mi × a						(2.29)
где i- порядковый номер наблюдения
				n
				∑ti
	mi	=		i=1			(2.30)
					n
				n
			∑ yi
	my	=	i=1				(2.31)
				n

где yi – фактическое значение спроса; ti- номер периода в наблюдении (номер i); n- количество рассматриваемых периодов.

Для выполнения расчетов воспользуемся таблицей в программе MS EXCEL (смотри рисунок 2.1).

Рис. 2.1. Определение параметров прогнозирования по методу наименьших квадратов.

Определяем α и b по формулам (2.28) и (2.29)

α=546,22/126,50=4,3 b= 219-6,5*4,3= 191,05

Эмпирическая линия регрессии имеет вид:

y = 4,3t + 191,05

Так как параметр α=4,3 делается вывод о том, что спрос в течении каждого месяца увеличивался в среднем на 4,3 единицы. Параметр b=191,05 показывает, что средний сглаженный спрос в начале базового периода при t=0 был 191,05 условных единиц. Подставив в формулу

y = 4 ,3t + 191 ,05

значения t=13,14,15 получим средний ожидаемый спрос на 13,14 и 15 месяцы.

y13= 4,3*13+191,05 =246,95 y14= 4,3*14+191,05= 251,25 y15= 4,3*15+191,05= 255,55

Произведем оценку погрешности прогноза. Для этого определим стандартное отклонение, которое в первом приближении можно принять в качестве оценки среднего квадратического отклонения ошибки прогнозирования.

						1 / 2
			n	2
			∑ ( y (ti ) − yi )			(2.32)
S	y	=	i =1
			n −1

где y(ti)- расчетное значение в i-ой точке, вычисленное по полученной формуле y= 4,3t+191,05, yi- фактическое значение спроса в i-ой точке, взятое из таблицы исходных данных. Для определения параметра Sy воспользуемся таблицей (рис. 2.1).

Подставив значение y(ti) и yi получим:

Sy =(2758/11) ½=15,8

Принимая во внимание, что ошибка прогнозирования подчиняется нормальному закону распределения, можно считать, что с вероятностью, близкой к 1, фактический спрос в каждой точке ti будет находиться в ин- тервале(y(ti)-45; y(ti)+45) по правилу 3σ, а с вероятностью 0,95 в диапазоне

(y(ti)-30; y(ti)+30) по правилу 2σ.

Данные зависимости спроса от времени представлены в таблице

(табл. 2.3).

Таблица 2.3.

Данные зависимости спроса от времени по методу наименьших квадратов с учетом погрешности с вероятностями 0,95 и 0,98.

X	1	2	3	4	5	6	7	8	9	10	11	12
Y	180	198	209	208	220	250	210	220	223	240	210	260
Y(ti)	195	200	204	208	213	217	221	225	230	234	238	243
Y(ti)-s(0.98)	150	155	159	163	168	172	176	180	185	189	193	198
Y(ti)+s(0.98)	240	245	249	253	258	262	266	270	275	279	283	288

Y(ti)-s(0.95)	165	170	174	178	183	187	191	195	200	204	208	213
Y(ti)+s(0.95)	225	230	234	238	243	247	251	255	260	264	268	273

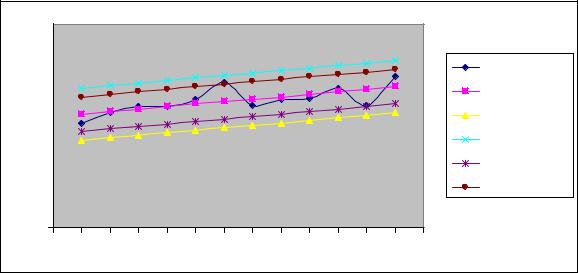
По рассчитанным параметрам строятся графики (рис. 2.2.)
350
300													Y
250
													Y(ti)
200													Y(ti)-s(0.98)
150													Y(ti)+s(0.98)
100													Y(ti)-s(0.95)
													Y(ti)+s(0.95)
50
0
0	1	2	3	4	5	6	7	8	9	10	11	12	13
Рис. 2.2. График зависимости спроса от времени с учетом погрешности по мето-

ду наименьших квадратов с вероятностями 0,95 и 0,98.

Определение уравнения регрессии второго порядка.

Для определения параметров эмпирической зависимости, выраженной уравнением регрессии второго порядка в виде

y = a0 + a1 x + a2 x 2

необходимо составить систему уравнений:

	n		2		n
			n
na0 + a1 ∑ xi + a2			∑ xi =		∑ yi ;
	i =1	2	i =1		i =1
	n			n	3	n
		n
a	0 ∑ xi + a1	∑ xi	+ a2 ∑ xi = ∑ xi				yi	;
	i =1	i =1	i =1			i =1		(2.33)
	n	n		n		n
a	0 ∑ xi 2 + a1 ∑ xi 3 + a2 ∑ xi 4 = ∑ xi 2 yi .
	i =1	i =1		i =1		i =1

Суммы, входящие в систему (2.33), удобно вычислять в программе MS EXCEL, пользуясь схемой (рисунок 2.3).

Рис.2.3. Расчет параметров уравнения 2-ой степени по методу наименьших квадратов.

Определив суммы, входящие в систему уравнений, получим:

12 * a	0	+ 78 * a + 650 * a			2	= 2628
			1
78 * a	0	+ 650 * a		+ 6084 * a			2	= 17702
			1
650 * a		0	+ 6084 * a + 60710 * a						2	= 149964
				1

Далее решаем систему уравнений MS EXCEL.

Решение будет заключаться в умножении обратной матрицы коэффициентов при неизвестных на матрицу свободных членов. Эти операции можно выполнить последовательно, т.е. сначала определить обратную матрицу коэффициентов при неизвестных при помощи функции МОБР, а затем полученную обратную матрицу умножить на матрицу свободных членов, при помощи функции МУМНОЖ, в диалоговом окне которой вызывается встроенная функция у первого массива, где в свою очередь вызывается функция обращения и вводится матрица коэффициентов. Для второго массива диалого-

вого окна функции МУМНОЖ вводится диапазон матрицы свободных членов. Ввод заканчивается комбинацией клавиш <Shift>+<Ctrl>+<Enter>. Например для нашего случая (рис.2.4.), матрица коэффициентов записана в диапазоне С27:Е29, а матрица свободных членов- в диапазоне Н27:Н29, формула выглядит следующим образом:

{=МУМНОЖ(МОБР(С27:Е29);Н27:Н29)}

Рис.2.4. Решение системы линейных уравнений.

В результате уравнение регрессии второго порядка имеет следующий вид:

y = a0 + a1ϕ1 (ti )+ a2ϕ2 (ti )= 180,68 + 8,67t - 0,33t 2

Определяем прогноз на 13 месяц:

y13 = 180,68 + 8,67 ×13 - 0,33 ×132 = 237,62

Погрешность определяется так же, как для уравнения первой степени.

2.2.2. Применение метода Чебышева для прогнозирования спроса.

Для построения многочлена воспользуемся вспомогательной таблицей

(табл.2.3.), выполненной в MS Excel:

Таблица 2.3.

Промежуточные вычисления для построения многочлена и определения погрешностей по методу Чебышева.

ti	yi	ti2	ti3	ti4	tiy	ti2y	yi2		yit			(yit-		yit			(yit-
												yi)2					yi)2
1	180	1	1	1	180	180	32400	195			229		189			79
2	198	4	8	16	396	792	39204		199			2		197			2
3	209	9	27	81	627	1881	43681	204			27		204			28
4	208	16	64	256	832	3328	43264	208			0		210			4
5	220	25	125	625	1100	5500	48400	212			56		216			18
6	250	36	216	1296	1500	9000	62500		217			1100		221			853
7	210	49	343	2401	1470	10290	44100	221			125		225			229
8	220	64	512	4096	1760	14080	48400	226			30		229			77
9	223	81	729	6561	2007	18063	49729		230			47		232			77
10	240	100	1000	10000	2400	24000	57600	234			34		234			35
11	210	121	1331	14641	2310	25410	44100	239			814		236			660
12	260	144	1728	20736	3120	37440	67600		243			293		237			546
78	2628	650	6084	60710	17702	149964	580978	2628			2758		2628			2609

Построение многочлена первой степени.

Согласно (2.10)

ϕ 0 (t ) = 1

Находим многочлен ϕ 1 ( t )			по формуле (2.			18)
		n		78
ϕ1 (t) = t −	1	∑ xi	= t −		= t − 6.5 .
	n
		i=1	12

Согласно (2.17)

		n
α1	= −	∑ti	= −	78	= −6.5 .
		i=1
		n
			12

По формуле (2.14) находим α 0

α0 = 2628 = 219 12 .

Уравнение 0 степени будет равно:

y = α 0ϕ0 (x) = 219(1) = 219 .

Найдем а1 по формуле (2.14)

	n	y ϕ 1 (t i )
	∑			620
a 1 =	i = 1		=		= 4 . 34
	n
	∑	[ϕ 2 (t i )]2		143

i = 1

где:

	n		n
	∑ y(ϕ1 )ti	=	∑
	i=1		i=1
	n		2
		(ti	)]
	∑[ϕ1
	i=1

n

(ti yi ) + α1 ∑ yi = 17702 + (−6,5)2628 = 620

		i=1
	n	2
		) + α1 ∑ti = 650 + (−6,5)78 = 143
	= ∑(ti
	i=1

Многочлен первой степени будет равен:

y = α0 + a1ϕ1 (t ) = 219 + 4,34(t − 6,5) .

Окончательно

y=219 + 4,34t - 28,21 = 4,34t + 190,79.

Пользуясь полученным уравнением, определяем в следующем (13) месяце:

y13 = 4,34 ×13 +190,79 = 247 .

Если точность результатов по этой формуле достаточна, обработка на этом может быть закончена.

Построение многочлена второй степени.

Если необходимо построить многочлен второй степени, необходимо сначала отыскать выражение для многочлена ϕ2 (t) и коэффициент a2 .

Для этого по формулам (2.23) находим β2иγ2

β

= −

∑n

ti [ϕ1 (ti

)]2

= −

929,5

= 6,5

2

i=1

n

(ti )]

∑[ϕ1

143

2

i=1

,

γ2

= −

∑n [ϕ1 (ti

)]2

= −

143

= −11,92

i=1

n

12

,

где согласно формулам (2.24):

n

2

n

n

n

[ϕ1 (ti )]

(ti )= 6084 + (− 6,5)650 + (−6,5)143 = 929,5

∑ti

= ∑ti3 +α1 ∑ti2

+α1 ∑tiϕ1

i=1

i=1

i=1

i=1

n

2

n

n

= 650 + (− 6,5)78 =143

∑[ϕ1 (ti )]

= ∑tt2

+α1 ∑ti

i=1

i=1

i=1

Многочлен ϕ2(t) определим по формуле (2.20)

ϕ2 (ti )= (t + β2 )ϕ1 (ti )+γ 2ϕ0 (ti )

ϕ2 (ti )= (t −6,5)(t − 6,5)−11,92 = t 2 −13t + 30,33

Представим многочлен в форме:

								ϕ2 (ti )= t 2 + kt + p .
Определим a2 по формуле (2.14)
				n	(ti )
		=		∑ yiϕ2			= − 454,76 = −0,34
a	2			i=1
				∑n [ϕ2 (ti )]2
							1332,5
				i=1				,
где
n				n			n	n
∑yiϕ2 (ti			)= ∑ti2 yi			+ k ∑ti yi		+ p∑yi =149964	+ (−13)17702	+ (30,33)2628 =
i =1				i =1			i =1	i =1

= −454,76