Северо-Западный государственный

университет им. И. И. МечниковаКафедра медицинской информатики и физики

Малевская И.И. Майоров Е.Е. Тихомирова А.А

Методическое пособие для студентов с примерами и задачами

ОСНОВЫМАТЕМАТИЧЕСКОГО АНАЛИЗА

КРАТКИЙ КУРС

Северо-Западный государственный

университет им. И. И. МечниковаКафедра медицинской информатики и физики

Малевская И.И. Майоров Е.Е. Тихомирова А.А

Методическое пособие для студентов с примерами и задачами

ОСНОВЫМАТЕМАТИЧЕСКОГО АНАЛИЗА

КРАТКИЙ КУРС

СОДЕРЖАНИЕ

Предисловие 3

Часть I

ДИФФЕРЕНЦИРОВАНИЕ

Определение производной. Правила дифференцирования. Таблицапроизводных

ДИФФЕРЕНЦИРОВАНИЕ 5

ПОЛНЫЙ ДИФФЕРЕНЦИАЛ 25

C = 0. 56

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 75

Математические методы имеют существенное значение длябиологии и медицины. Процессы, происходящие в живыхорганизмах настолько сложны и изменчивы, что дляудовлетворительного описания биологического и медицинскогоматериала нужны сложные математические модели, а дляобработки и объяснения результатов могут потребоваться довольносложные математические и вычислительные методы.

Возможно, что студентам, с робостью приступающим кизучению элементов высшей математики и имеющим слабыематематические способности, освоение материала весьмазатруднительно. Но есть надежда, что изучаемый курс математикии статистики даст им возможность разобраться в основахматематического анализа, а также понять роль теории вероятностейи статистики в изучении медицинских и биологических явлений,решать элементарные дифференциальные уравнения при изучениикурса медицинской и биологической физики.

Часть 1

ДИФФЕРЕНЦИРОВАНИЕ

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ. ПРАВИЛАДИФФЕРЕНЦИРОВАНИЯ. ТАБЛИЦА ПРОИЗВОДНЫХ

Определение 1. Производной функции f(x) в точке х называется

Производная - это предел отношения приращения функции к приращениюее аргумента при стремлении приращения аргумента к нулю, характеризуетскорость изменения функции. Функция, имеющая конечную производную,называется дифференцируемой функцией.

Процесс вычисления производной называется дифференцированием.Из определения следуют основные правила дифференцирования:

1. (const)' = с' ⁼ 0.

Производная любого постоянного числа равна нулю.

Примеры:

• (5)' = 0;

• (-8)' = 0;• (232)'= 0.

2. (х)' = 1.

Производная аргумента равна 1.

2. (с u)' = с u'.

Постоянное число можно выносить за знак производной.Пример:

• (5 х)' = 5 х' = 5 • 1=5.

2. (u + v - w + ... + s)' = u' + v' - w' + ... + s'.

Производная алгебраической суммы любого числа слагаемых равна этой жеалгебраической сумме производных слагаемых.Примеры:

• (Зх - 8)' = (Зх)' - (8)' = 3• 1-0 = 3;

5. Если

сложная функция и

, где u — любая функция.

Если u = х, то (хn)' = n хn-1.

Примеры:

Примеры:

Производная синуса сложной функции равна произведениюпроизводной этой сложной функции на косинус этой функции.Если u = х, то (sin х)' = cos х .Примеры:

Производная степени функции un равна произведению показателястепени на функцию, в степени на единицу меньше, на производнуюсамой функции.

Производная косинуса сложной функции равна минус произведениюпроизводной этой сложной функции на синус этой функции.Если u = х, то (cos х)' = - sin х.Примеры:

Производная произведения равна сумме произведений производнойпервого сомножителя на второй и производной второго сомножителяна первый.Примеры:

Пример 1. Найти производную функции у = Зх + 5:Решение:

Пример 2. Доказать, используя лишь определение, что

Доказательство:

что требовалось доказать.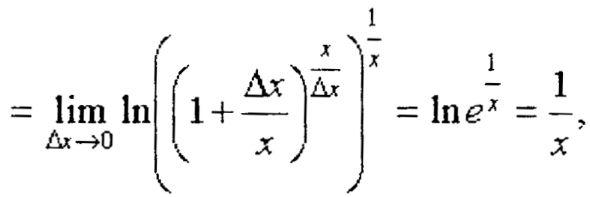

Вынося в последнем равенстве логарифм за знак предела, мы

Заметим, что

воспользовались непрерывностью функции

тоже

условие

гарантирует, что при достаточно малом

что необходимо для существования

будет

ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИ

И

Пусть дана функция

сложная функция аргумента

Считаем, что функции

дифференцируемые по своим аргументам,

находится по следующей формуле:

тогда производная функции

Решение: Обозначим

Пример а). Найдите производную функции

Воспользуемся формулой

Найдем:

Пример в). Найдите производную функции:

Решение:

Решение:

Пример с). Найдите производную функции:

ПРИЕМЫ ДИФФЕРЕНЦИРОВАНИЯ

1. Для функций, представляющих собой громоздкие произведения ичастные различных степенных выражений, удобно, а для показательно-степенных функций, где от переменного зависят как основаниестепени, так и ее показатель, - необходимо применять приемлогарифмического дифференцирования

.

Этот прием основан на соотношении

Пример№1. Найти

где