Семестровые компьютерные задания

22

3. На рис. 3 построен вектор напряженности электрического поля для А = 12 и q > 0. Сначала в точке с координатой y = 0, самой правой по оси x, лежащей на заданном уровне, проведем касательную к эквипотенциальной линии. Вектор напряженности перпендикулярен к этой касательной. Направление вектора

E , в соответствии со знаком в формуле (1), соответствует направлению уменьшения потенциала (от большего потенциала к меньшему).

4. Теперь найдем величину вектора напряженности по формуле (1). Приблизительно модуль напряженности можно рассчитать как

E max min

r r

где - разность потенциалов ближайших уровней, r - расстояние между этими уровнями по линии, совпадающей с направлением напряженности. Таким образом, в нашем случае получаем

Е = 1/0.2= 5

23

3. Переменный ток. Колебательный контур

Краткое теоретическое введение

Как известно, сила переменного тока изменяется во времени по гармоническому закону. По такому же закону изменяется и напряжение в цепи. Начальную фазу всегда можно выбирать произвольно, ни на какие физически значимые результаты это не повлияет.

Существует три различных способа описания цепей переменного тока: а) с помощью комплексных функций от времени; б) с помощью тригонометрических функций времени (как в школьном курсе физики); в) с помощью дифференциальных уравнений.

Первый способ является самым удобным, т.к. позволяет для цепей переменного тока полностью сохранить те же приемы и методы (законы Ома, правила Кирхгофа, метод контурных токов, эквивалентных схем и т.д.), что применяются для цепей постоянного тока. Поэтому в дальнейшем мы будем использовать только метод комплексных функций (см. дополнение, п.1).

Закон Ома для участка цепи переменного тока имеет вполне стандартный

вид

I U / Z .

(1)

Единственное отличие от цепи постоянного тока в том, что сопротивление обозначают Z и называют импеданс, который в общем случае принимает комплексные значения. Чтобы подчеркнуть его комплексный характер, отметим, что импеданс имеет не только действительную часть (обычное активное сопротивление), но и мнимую часть (реактивное сопротивление). Одно и тоже комплексное число можно представить в трех формах (см. приложение 6):

	алгебраической	Z = a + i b;
	показательной	Z =		exp(i ) , где	arctan g	b	;
			a2 b2
						a

и тригонометрической

Z = 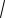a2 b2 cos i sin ,

где мнимое число i = √-1 .

Соответственно импеданс можно записать в одном из трех видах:

Z R iX 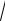R2 X 2 exp i = R2 X 2 (cos i sin ) , (2)

24

где arctg( XR ) . При проведении конкретных расчетов, в зависимости от удобства, выбирается та или иная форма представления комплексных чисел.

Носителями активного сопротивления являются обычные резисторы, а реактивного – катушки индуктивности и конденсаторы. Примем пока начальную фазу напряжения за нуль, т.е. зададим его зависимость от времени в виде

U U0 exp(i t) U0 (cos t isin t) ,

(3)

где - циклическая частота внешнего напряжения. Таким образом, комплексные величины можно интерпретировать как вектора, вращающиеся с течением времени на плоскости xy с частотой ω в системе координат, где по оси х откладываются действительные величины, а по оси y - чисто мнимые. Длины векторов при этом совпадают с амплитудами соответствующих колебаний.

Рассмотрим простейшие случаи приложения напряжения (3) к различным типам импедансов.

1) Если сопротивление участка чисто активное Z = R, то согласно (1)

I	U0 exp(i t)	I	0 exp(i t) .	(4)
	R

Это означает, что амплитуда тока через активное сопротивление от частоты не зависит, а фаза тока совпадает с фазой напряжения.

2) Импеданс катушки индуктивности задается в виде

X L	i L L exp(i		) .	(5)
	2

После подстановки в закон Ома (1) это дает для тока

U		0	exp(i t)			U	0	exp(i t)
I											I0 exp(i t i		) .	(6)
			X									2
				L	L exp i
									2

Из (6) следует, что амплитуда тока через катушку обратно пропорциональна частоте, а фаза тока отстает от фазы напряжения на /2. Другими словами, катушка задерживает ток, как и должно быть из-за явления электромагнитной индукции. При переходе к постоянному току 0 ток формально неограниченно растет. Это также объяснимо, ибо катушка – просто свернутый в кольца хороший проводник и становится активным элементом только тогда, когда магнитный поток (а, значит, и ток) через нее меняется.

3) Импеданс конденсатора задается формулой

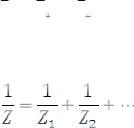
			25
XС		1		1	exp( i		) .	(7)
		i С		С
					2

После подстановки в (1) получаем для тока через конденсатор

I

U0 exp(i t)

U0 exp(i t) C

I0

exp(i t i

)

.

(8)

XC

i

2

exp

2

Из (8) видим, что амплитуда тока через конденсатор прямо пропорциональна частоте, а фаза тока опережает фазу напряжения на /2. При переходе к постоянному току 0 амплитуда тока уменьшается до нуля. И это хорошо объяснимо, т.к. конденсатор – разрыв в цепи, заполненный диэлектриком, и постоянный ток через него не идет.

В общем случае расчет цепей переменного тока может быть проведен в соответствие с обычными правилами последовательного и параллельного соединения элементов. В частности, при последовательном соединении элементов для импеданса цепи имеем

… ,

а при параллельном соединении соответствующая формула принимает вид

При конкретных расчетах в этом случае нужно иметь в виду, что все операции с комплексными числами проводятся по правилам обычной алгебры, с той лишь разницей, что теперь подобные члены собираются с учетом существования действительных и мнимых частей. В частности, пусть

		Z1 = a1 + i b1,		Z2 = a2 + i b2.
Тогда имеем (см. приложение 6)
1)	Z1±Z2 = A+i B,	где	A = a1±a2;	B = b1±b2
2)	Z1Z2 = A+i B,	где	A= a1a2 - b1b2; B = a1b2+b1a2
3)	Z1/Z2= A+i B,	где	A = (a1a2 + b1b2)/C; B = (-a1b2 + b1a2)/C;
			где	C = (a2)2+(b2)2.

В результате для полного импеданса цепи получим комплексное выражение типа (2). После подстановки его вместе с (3) в (1) для тока в цепи имеем

26

	I		U	0		exp(i t i ) .	(9)
			R2 X 2

Как видно из (9), ток, вообще говоря, сдвинут по фазе относительно напряжения. Амплитуда же тока через реактивную составляющую импеданса Х зависит от частоты внешнего напряжения . Вспомним, что переменный ток – это вынужденные электромагнитные колебания под действием гармонической внешней силы U(t). Для таких систем характерно явление резонанса – роста амплитуды колебаний при приближении частоты внешнего напряжения к собственной частоте цепи 0 . Зависимость I( ) называют резонансной кривой, и ее исследование – одно из заданий в данной работе.

Векторная диаграмма – это наглядное изображение колебательного процесса. В таких диаграммах использован тот факт, что длина проекции вращающегося с постоянной угловой скоростью вектора длиной А меняется по гармоническому закону

,

аналогичному закону изменения переменного тока и напряжения. Рассматривая импедансы отдельных элементов и токи в них как векторы и используя правила векторной алгебры, можно рассчитать и изобразить на диаграмме полный импеданс и полный ток в цепи.

0

A

x

При этом по горизонтальной оси можно отложить, например, внешнее напряжение, фаза которого принята за нуль; тогда угол, который образует с горизонтальной осью построенный вектор результирующего тока в цепи, даст сдвиг фаз между током и напряжением, а длина этого вектора – амплитуду тока в цепи.

При расчетах нужно помнить, что применение комплексных чисел обусловлено лишь необходимостью упростить промежуточные расчеты. Результирующие значения напряжений и токов всегда действительны, что подтверждается их измеримостью.

27

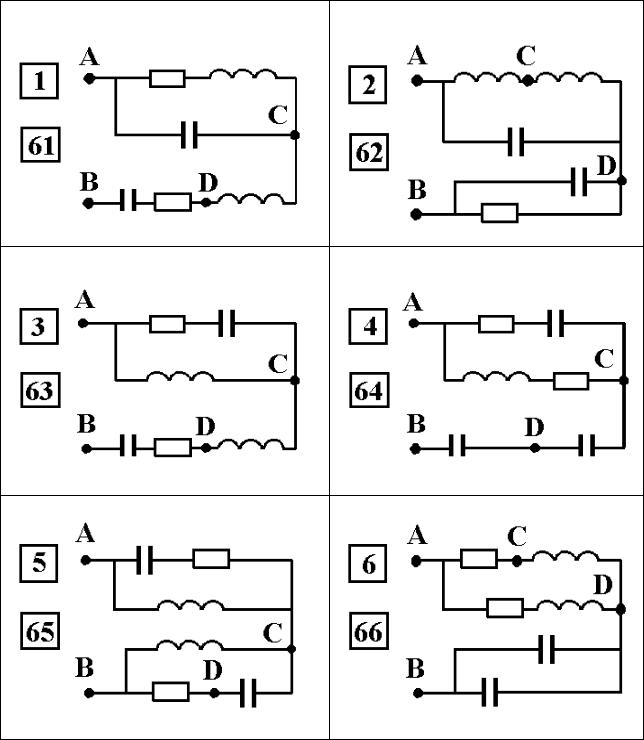
Варианты индивидуальных семестровых заданий

28

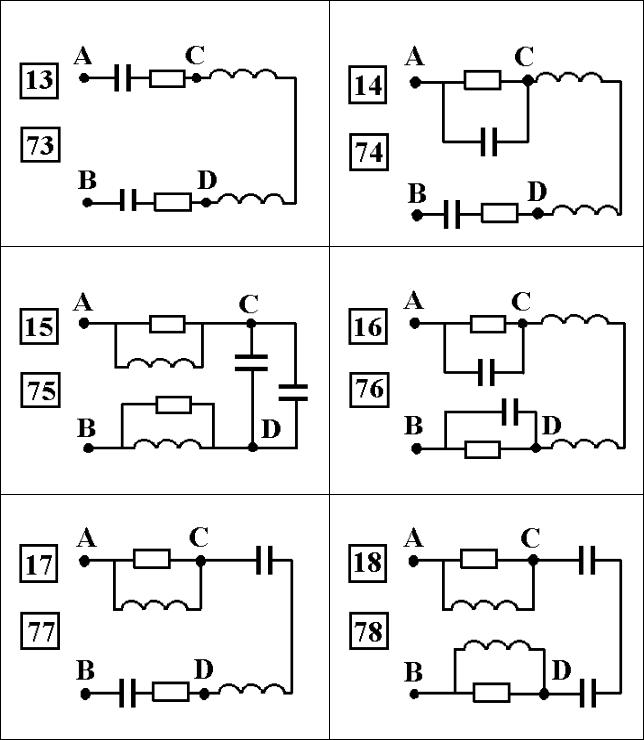
29

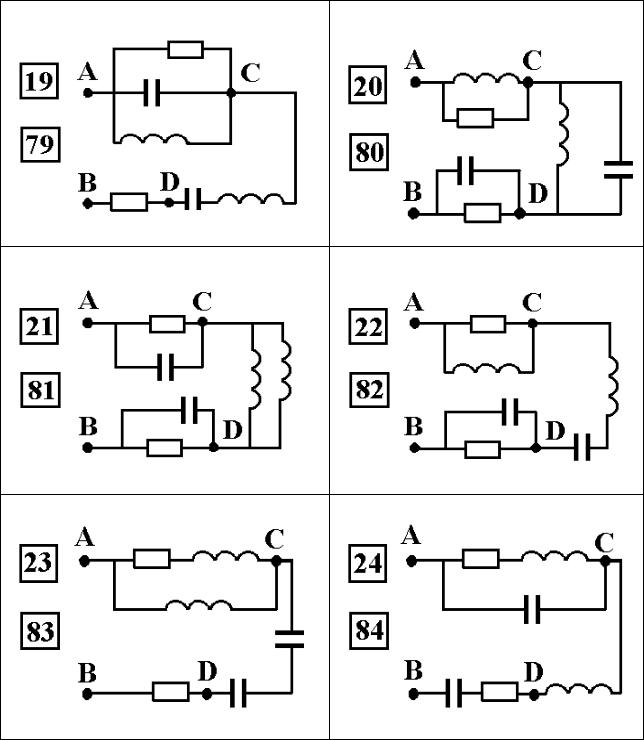
30

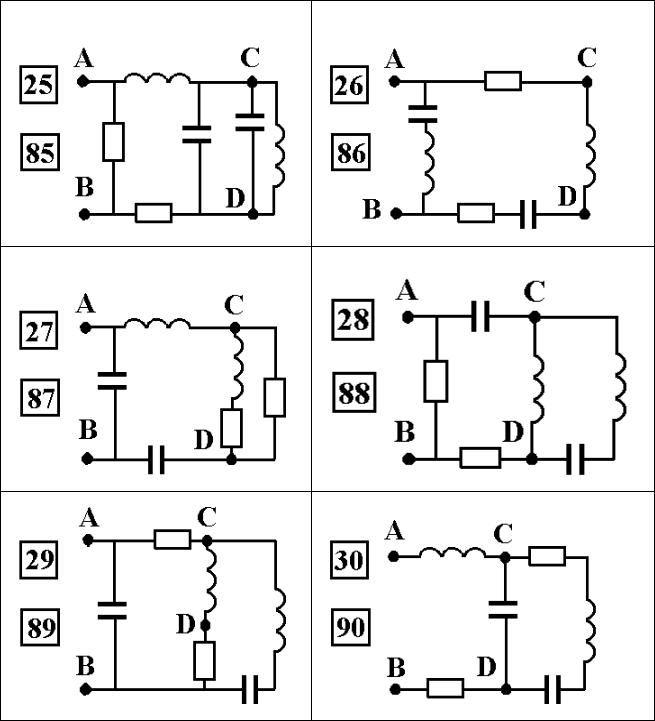
31