Тема 5. Целочисленное программирование Постановка задачи

Значительная часть задач оптимального планирования по смыслу может иметь решения только в целых числах. Такие задачи связаны с определением количества единиц неделимой продукции, например, числа станков при загрузке оборудования, численности работников в структурных подразделениях предприятия и т.д.

Такие задачи решаются методами целочисленного программирования, где общая постановка задачи линейного программирования дополняется требованием о том, чтобы найденные переменные в оптимальном плане были целыми.

Если функция и ограничения в таких задачах линейны и на переменные задачи наложено условие целочисленности, то такие задачи называются задачами линейного целочисленного программирования.

Задача линейного целочисленного программирования формулируется следующим образом: найти такое решение (план) , при котором линейная функцияпринимает максимальное или минимальное значение при ограничениях

Если не на все переменные наложено условие целочисленности, то такие задачи называются частично целочисленными.

В настоящее время наиболее широкое применение находят два основных метода решения задач целочисленного программирования:

а) метод отсечений;

б) комбинаторный метод.

Методы отсечения используют оптимальные решения, найденные для задач линейного программирования, сужая область допустимых решений до целочисленных границ, т.е. отсекая нецелочисленные допустимые планы, получают решения задач целочисленного программирования.

Комбинаторные методы достигают решений задач целочисленного программирования, рассматривая возможные варианты целочисленных ограничений для задачи оптимизации.

Графическое решение задачи целочисленного линейного программирования

Рассмотрим случай, когда число неизвестных равно двум. Для решения задачи графическим методом прежде строят многоугольник решений без условия целочисленности. Условию целочисленности переменных удовлетворяют не все координаты точек области допустимых решений, поэтому область допустимых решений ослабленной задачи (без условия целочисленности) заменяется на выпуклый многоугольник, содержащий только допустимые точки с целочисленными координатами. Чтобы найти максимум или минимум целевой функции на выпуклой оболочке строят вектор градиент С(с₁, с₂). Передвигая прямую Z =c₁x₁+c₂x₂ в направлении вектора С, в результате чего находят точку, в которой целевая функция принимает оптимальное значение. Затем определяем координаты точки экстремума функции и вычисляем значение целевой функции в этой точке.

Пример. Найти максимальное значение целевой функции при заданных ограничениях:

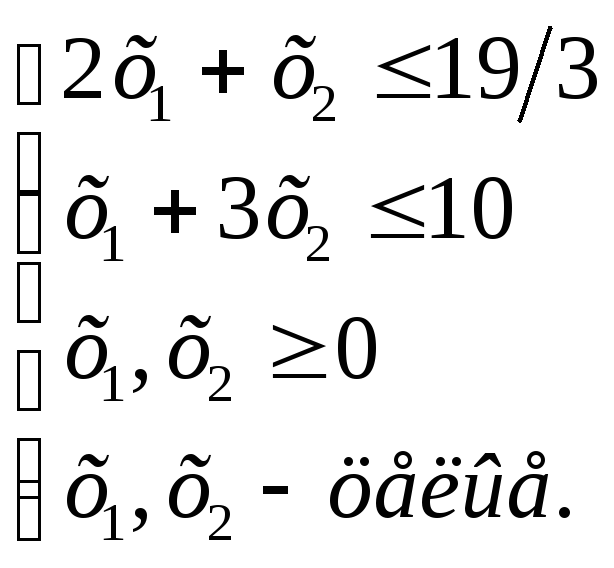
Решение. Поскольку число неизвестных задачи равно двум, то решение данной задачи можно найти графически. Для этого построим многоугольник решений задачи без условия целочисленности.

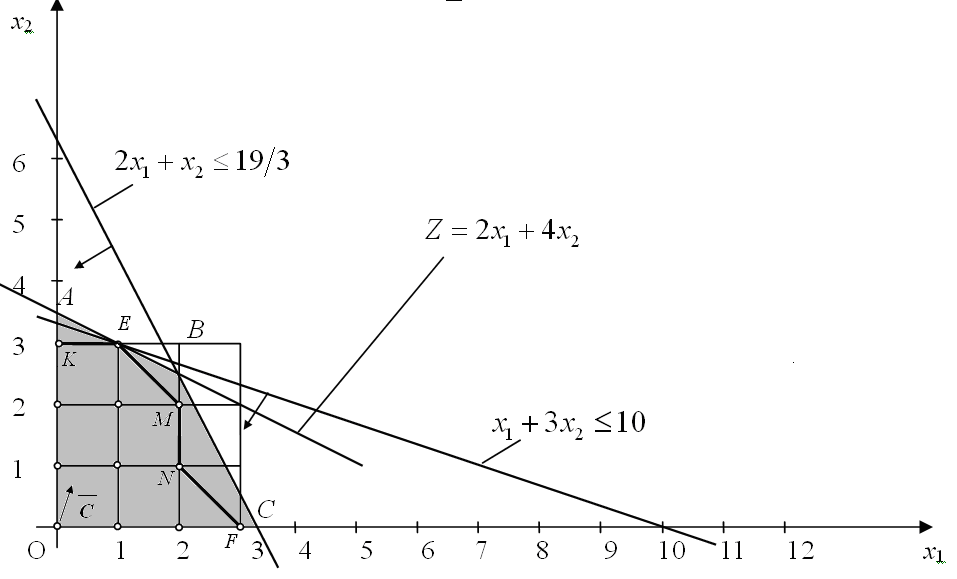
Условию целочисленности удовлетворяют лишь 12 точек, отмеченных на рисунке. Чтобы найти точку, координаты которой определим решение исходной задачи, заменяя многоугольник ОАВС многоугольником OKEMNF, содержащий все допустимые точки с целочисленными координатами.

Для определения максимального значения целевой функции на многоугольнике OKEMNF построим вектор градиент С(2; 4) и прямую . Построенную прямую передвигаем в направлении вектора градиента до тех пор, пока она не пройдет через последнюю общую точку ее с этим многоугольником. Координаты полученной точки Е(1; 3) и являются оптимальным решением задачи, а значение целевой функции в ней F_max=14 является максимальным.