2.1.1. Распределение температур в телах на стационарном режиме.

Теплопроводность плоской стенки .

Однородная стенка. Достаточно просто описывается распределение температур в плоской однородной стенке с постоянным коэффициентом теплопроводности λ. Считаем известными температуры на границах стенки – t₁ и t₂ (рис. 2.2)

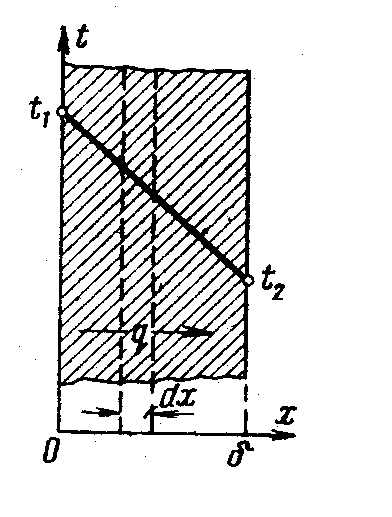
Рис.2.2 Изменение температур в плоской стенке

Выделим на расстоянии х и dx две изотермические поверхности. По закону Фурье :

q = - λ или dt = - dx (2.3)

В условиях постоянства λ и q интегрирование (2.3) дает:

t = -x + С (2.4)

Постоянную интегрирования С найдем из граничных условий (температуры на границах стенки t= t₁ =С при х=0 и t = t₂ при х=δ). Откуда :

t₂ = -δ + t₁ (2.5)

Удельный тепловой поток через стенку определится:

q = (t₁ - t₂) = (2.6)

Видно, что удельный тепловой поток через плоскую стенку прямо пропорционален коэффициенту теплопроводности λ и разности температур наружных поверхностей Δt и обратно пропорционален толщине стенки δ.

Уравнение (2.6) описывает теплопроводность плоской стенки и позволяет по известным трем параметрам найти четвертый:

λ= ; ;

Отношение называют тепловой проводимостью, а обратную величину - тепловым или термическим сопротивлением (из-за аналогии с распространением электричества).

Из уравнения (4) можно получить формулу определения температуры внутри стенки на любом расстоянии х:

t_x = t₁ - (2.7)

Уравнение (2.7) показывает, что распределение температур в плоской стенке линейное (при условии постоянства коэффициента теплопроводности). Если уточнить формулу (2.7), введя линейную зависимость коэффициента теплопередачи (2.2) от температуры, то получим:

q = -λ(t) = -λ₀ (1 + bt) (a)

Разделив переменные и произведя интегрирование, получим:

qx = - λ₀ (t + bt²/2) + C (b)

Подставляя в (а) граничные значения переменных, получим:

x = 0 t =t₁ 0 = - λ₀ (t + bt²/2) +C; (c)

при

x = δ t = t₂ qδ= - λ₀ (t + bt²/2) +C (d)

Вычитая из второго равенства (d) первое (с), получим

, (е)

откуда

(2.8)

Полученная формула (2.8) по сравнению с (2.6) несколько сложнее. При выводе (2.6) принимался постоянным коэффициент теплопроводности λ. Если его заменить осредненным значением λ_{m ,} то из равенства правых частей (2.8) и (2.6) следует:

λ_m = λ₀ = (g)

Следовательно, если λ_m определяется по среднеарифметическому из граничных значений температур стенок, то формулы (2.6) и (2.8) равнозначны. Решая (b) относительно t и подставляя значение С из (с), получим зависимость:

(2.9)

Температура стенки в соответствии с (2.9) изменяется не по прямой, а по кривой. Если коэффициент b положителен, то выпуклость кривой направлена вверх, если же отрицателен, то вниз.

Для большинства инженерных задач толщина стенок мала и с достаточной степенью точности можно считать распределение температур в стенке по линейному закону, принимая осредненное значение λ_m по граничным значениям температур стенок.

Многослойная плоская стенка.

В конструкциях часто встречаются многослойные стенки. Нередко наружная стенка является теплоизолятором для снижения утечек тепла или снижения температуры стенки в случае возможного контакта с кожей человека. Теплоизоляцию вводят для снижения утечек тепла через стены домов и т.д.

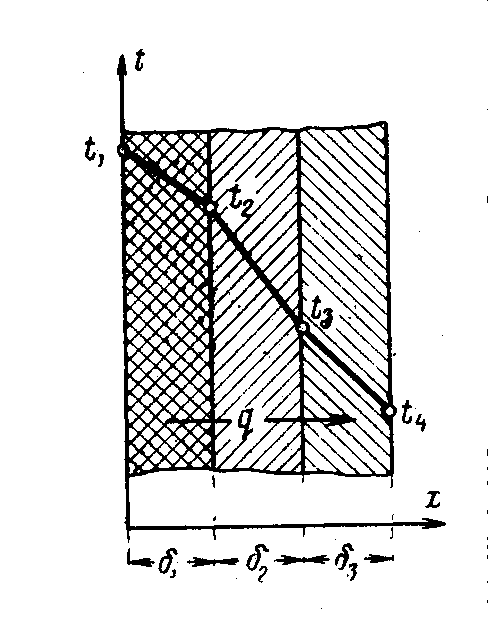
Рис. 2.3. Изменение температур в многослойной плоской стенке.

На рис.2.3 показано сечение трехслойной плоской стенки. Примем, что толщины слоев слева направо имеют обозначения – первого δ₁, второго δ₂ и третьего δ₃. Соответственно коэффициенты теплопроводности слоев обозначим λ₁, λ₂ и λ₃. Кроме того, известны температуры наружных поверхностей соответственно t₁ и t₄. Тепловой контакт между поверхностями считаем идеальным, температуры в местах контакта обозначим t₂ и t₃.

Удельный тепловой поток на стационарном режиме q постоянен и для всех слоев одинаков. Поэтому на основании (2.6) записываем:

;  ;  (h)

. 

Найдем разности температур в каждом слое:



 ( i )



Сумма изменений температур в каждом слое составляет полный температурный напор. Складывая правые и левые части уравнения (i) , получаем:

( j )

Из соотношения ( j ) можно определить удельный тепловой поток:

q = (2.10)

Можно написать в общем виде, для многослойной стенки:

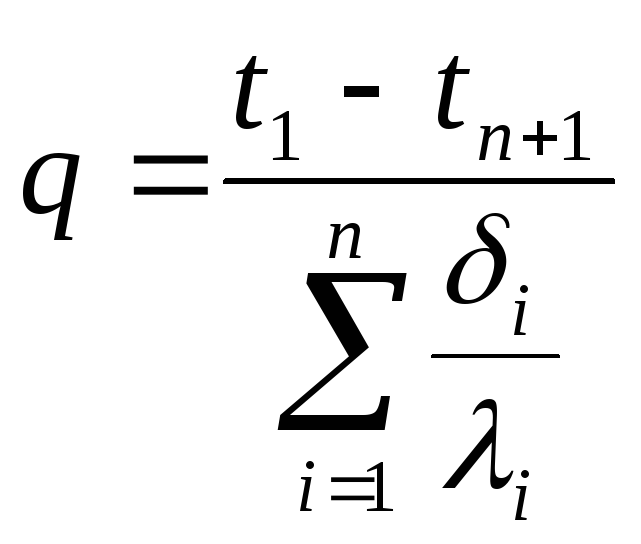(2.11)

Каждое слагаемое знаменателя в (2.10) представляет собой термическое сопротивление слоя, то из уравнения следует, что общее термическое сопротивление многослойной стенки равно сумме частных термических сопротивлений (знаменатель равенства (2.11)).

Можно определить значения неизвестных температур t₂ и t₃, если значение теплового потока из (2.10) подставить в ( i ):



 (2.12)



Внутри каждого слоя температуры меняются линейно, но для всей толщины многослойной стенки – это ломаная линия, тангенс наклона каждого отрезка определяется коэффициентом теплопроводности слоя (рис. 3).

Иногда для оценочных расчетов вводят понятие эквивалентного коэффициента теплопроводности плоской стенки λ_экв , определяемого по зависимости:

(k)

Откуда можно найти:

λ_экв= (2.13)

Зная, например, значение температур в жилом помещении и на улице с помощью эквивалентного коэффициента теплопроводности можно оценить утечки тепла через плоскую поверхность стены.

Надо иметь в виду, что при выводе уравнений тепловых потоков для многослойной плоской стенки предполагалось, что имеет место хороший контакт соприкасающихся слоев. В реальной жизни невозможно обеспечить идеальное прилегание поверхностей и в стыках обязательно будут иметь место воздушные прослойки.

Рассмотрим уравнения тепловых потоков многослойной стенки с учетом контактного термического сопротивления.

Для слоя стенки с коэффициентом теплопроводности λ и толщиной δ уравнение удельного теплового потока записывается

Соотношение λ/δ называется тепловой проводимостью плоской стенки, а обратная величина δ/λ – внутренним термическим сопротивлением.

При наличии контактного термического сопротивления тепловой поток можно записать

Здесь R_к – контактное термическое сопротивление, создающее перепад температур .

Уравнение для разности температур и удельного теплового потока запишется:

,

Откуда

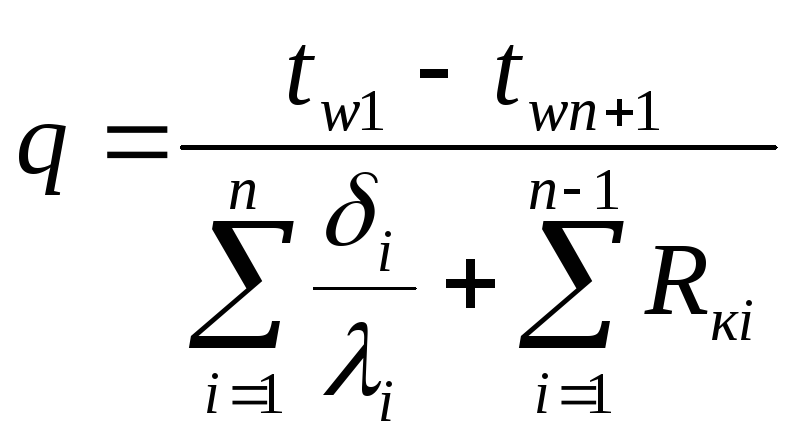
После определения суммарного теплового потока q перепады температур внутри слоев определяются из уравнения q = - (λ/δ)Δt , а скачки температур в стыках q = (1/R_кi )Δt.

Коэффициент теплопроводности воздуха на порядки отличается от теплопроводности твердых строительных материалов. Следовательно, с учетом воздушных прослоек термическое сопротивление многослойной стенки будет значительно выше. Строители сознательно вводят воздушные пустоты для увеличения теплового сопротивления стен.

Теплопроводность цилиндрической стенки.

Однородная цилиндрическая стенка.

Рассмотрим однородную цилиндрическую стенку (трубу) со следующими геометрическими размерами:

длина ℓ;

наружный радиус r₂

внутренний радиус r_1.

Примем, что коэффициент теплопроводности одинаков и равен λ, температуры наружной и внутренней стенок постоянны и равны соответственно t₂ и t₁, причем t₂ < t_1. Если считать, что изменение температуры будет иметь место только в радиальном направлении, то можно говорить об одномерном температурном поле. Говорят, что в этом случае применяются цилиндрические координаты, когда определяющим геометрическим параметром будет расстояние от оси цилиндра.

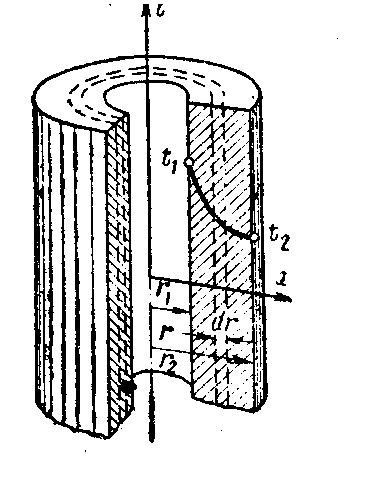
Рис.2.4. Однородная цилиндрическая стенка.

Выделим внутри стенки кольцевой слой текущего радиуса r и толщиной dr, ограниченный двумя изотермическими поверхностями, отличающимися на dt. По закону Фурье тепловой поток через этот слой определится:

Q = - (a)

Произведем разделение переменных:

(б)

Интегрирование уравнения (б) дает:

(в)

Если произвести подстановку значений заданных переменных на границах стенок (при r = r₁ t = t₁ и при r = r₂ t = t₂) и исключить постоянную С, можно получить расчетную формулу для цилиндрической стенки:

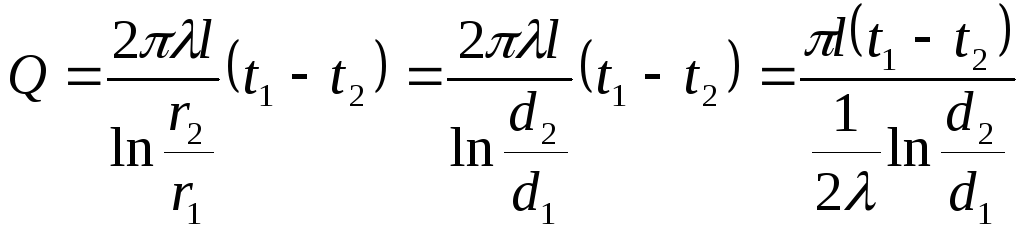(2.14)

Можно отнести для удобства найденный тепловой поток к площади одной из боковых поверхностей – внутренней или наружной или к длине трубы, тогда:

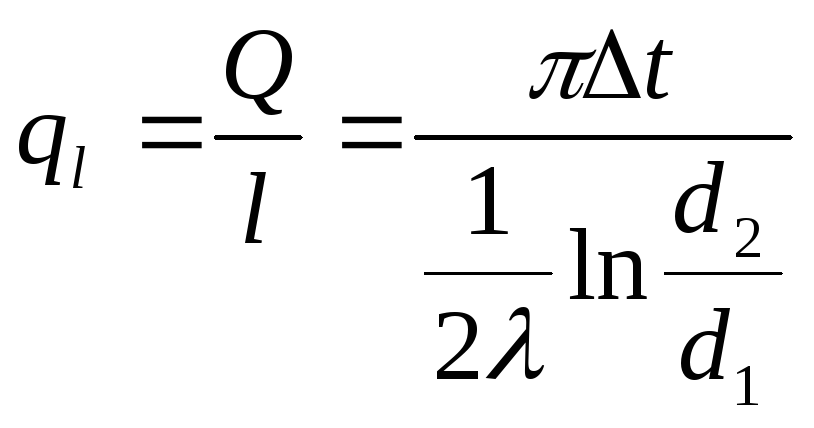; (2.15)

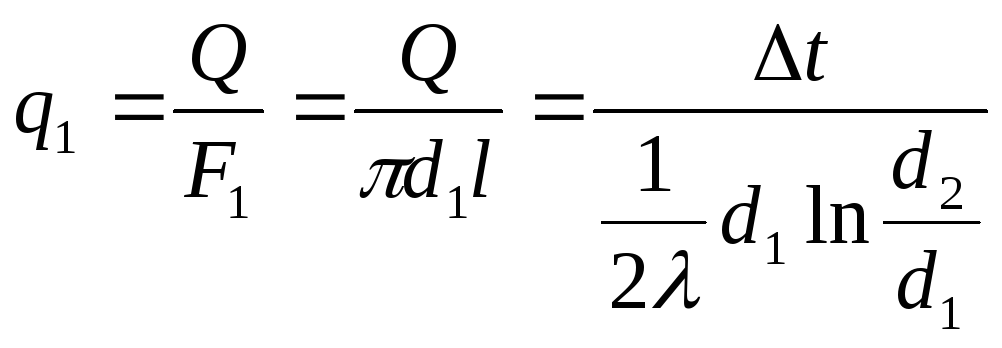; (2.16)

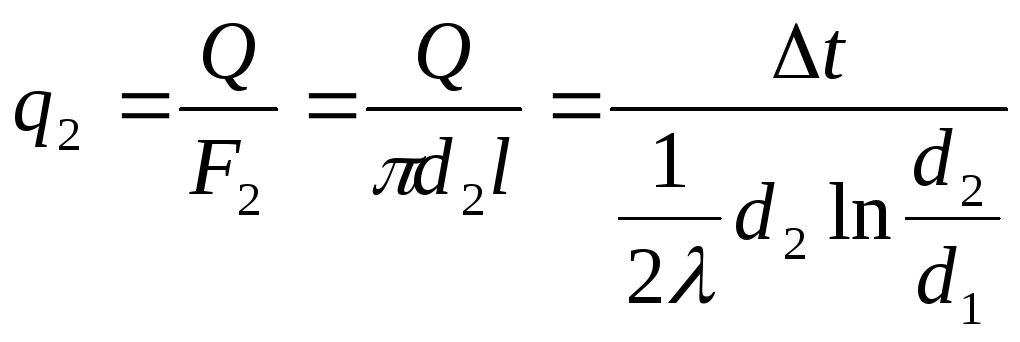(2.17)

Можно сделать вывод, что количество тепла, переданное в течение часа через цилиндрическую однослойную стенку прямо пропорционально коэффициенту теплопроводности λ, длине трубы ℓ и температурному напору Δt = (t₁ - t₂) и обратно пропорционально натуральному логарифму отношения внешнего диаметра d₂ к внутреннему d₁. Формула (2.14) справедлива и при обратном направлении теплового потока, когда t₁ < t₂.

Для цилиндрической стенки плотность теплового потока зависит от того, к какой поверхности мы будем относить суммарное количество тепла – к внешней или внутренней.

Уравнение для температурной кривой в цилиндрической стенке можно получит из (в):

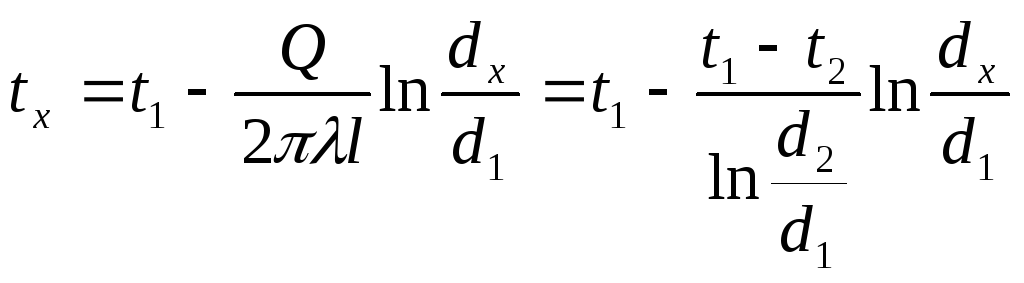(2.18)

При постоянном коэффициенте теплопроводности температура по толщине стенки изменяется по логарифмической кривой. Если принять линейную зависимость коэффициента теплопроводности от температуры, т.е. λ = λ₀(1+bt), то уравнение изменения температуры по толщине цилиндрической стенки примет следующий вид:

(2.19)

Многослойная цилиндрическая стенка.

Примем, что цилиндрическая стенка состоит из трех слоев материалов с разными коэффициентами теплопроводности.

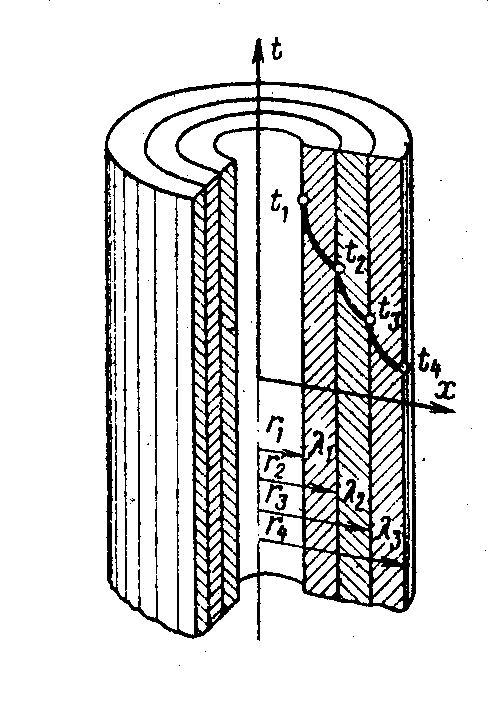
Рис.2.5 Распределение температур в многослойной цилиндрической стенке.

Известны:

радиуса цилиндров всех слоев (r_1, r₂ , r_3, r₄);

теплопроводности всех слоев (λ₁, λ₂ и λ₃);

температура внутренней поверхности стенки t₁;

температура наружной поверхности стенки t₄.

С учетом (15) запишем для каждого из трех слоев :

; 

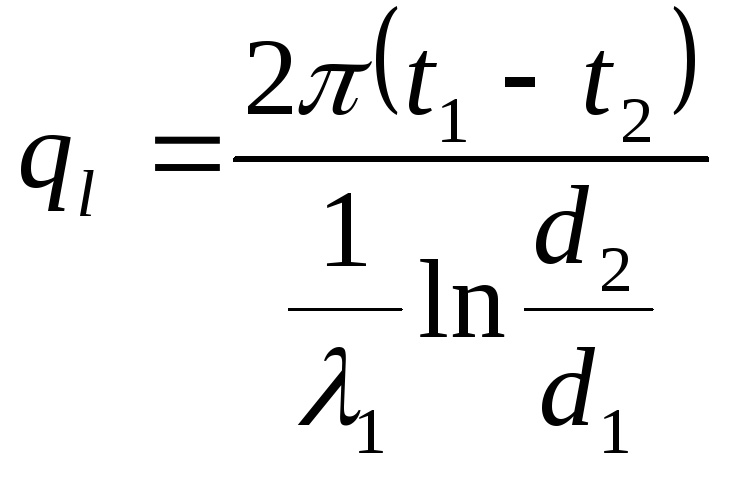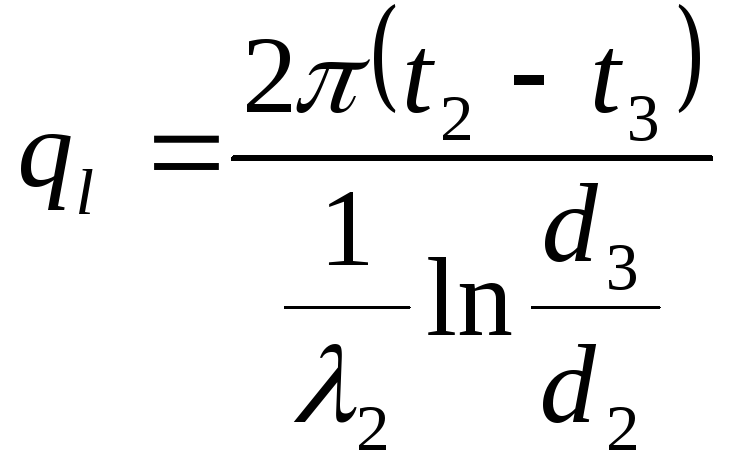;  (г)

. 

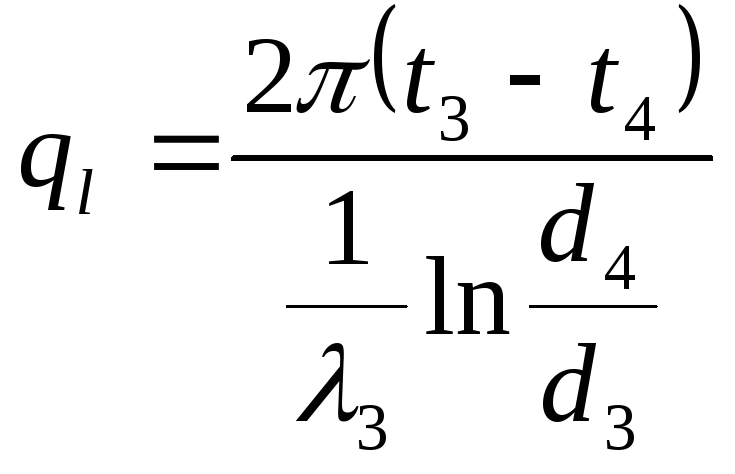Как и ранее найдем перепады температур по слоям

; 

;  (д)

. 

Сумма перепадов температур равна полному температурному напору :

, (е)

откуда определяем тепловой поток:

(2.20)

Для n – слойной стенки :

(2.21)

Значения неизвестных температур t₂ и t₃ поверхностей внутренних слоев можно найти с помощью (д):



 (2.22)

. 

В соответствии с (2.18) температура внутри каждого из слоев изменяется по логарифмическому закону. Для всей толщины стенки получается сложная система ломаных кривых

Однородная шаровая стенка.

Определим распределение температуры в однородном сферическом теле с постоянным значением коэффициента теплопроводности λ , имеющим внутренний радиус r₁,температуру внутренней поверхности t₁, наружный радиус r₂, температуру наружной поверхности t₂, причем t₂ < t₁ .

Рис.2.6. Однородная шаровая стенка.

Изотермические поверхности будут концентрическими сферическими поверхностями. Выделим внутри стенки сферический слой радиуса r и толщиной dr, ограниченный двумя изотермическими поверхностями. По закону Фурье тепловой поток:

(^,)

Разделяя переменные, получим:

(^,,)

Интегрирование второго уравнения дает:

(^,,,)

Подставляя в (^,,,) значения переменных на границах стенки (при r = r₁ , t = t₁ и при r = r₂ , t = t₂), а также исключая константу С, получаем расчетную формулу:

, (2.23)

где - толщина стенки.

Уравнение температурной кривой внутри однородной шаровой стенки можно получить из (^,,,) путем подстановки Q и C :

(2.24)

Распределение температур в шаровой однородной стенке подчиняется уравнению гиперболы.