Практика_5

Задание к практическому занятию № 5

ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ ЛИНЕЙНЫХ САУ

Цель практического занятия: изучение характеристик типовых динамических звеньев линейных систем автоматического управления (САУ).

Краткие теоретические сведения

Связь между выходным и входным сигналами определяется динамическими свойствами элемента управления, которые можно представить в виде передаточной функции W(s). Таким образом,

динамическим звеном называется любой элемент системы автоматического управления, имеющий определенное математическое описание, т.е. для которого известна передаточная функция.

х(t)

у(t)

элемент

а)

X(s)

Y(s)

W(s)

б)

Рис. 1. Элемент (а) и динамическое звено (б) САУ

Звенья, описываемые дифференциальными уравнениями не выше второго порядка, называют типовыми звеньями.

Для анализа характеристик типовых звеньев используются уравнения динамики, которые обычно записываются в виде передаточной функции в

изображениях Лапласа при обозначении s = p
W(s) = W(p) = Y(p) /X(p) =K(Tp+1)/(T22 p2 +T1 p +1).		(1)
Передаточную функцию системы можно представить в виде
произведения простых множителей и дробей:
K, Tp, 1/Tp,	Tp ± 1, 1/(Tp ± 1),
T2p2 ± 2ζTp + 1,	1/(T2p2 ± 2ζTp + 1),	(2)

где K- коэффициент передачи (или усиления), который является постоянным для линейного звена, T – постоянная времени (мера инерционности звена),

ζ – коэффициент демпфирования (затухания).

Сомножители представляют звенья: пропорциональное - K, дифференцирующее - Tp, интегрирующее - 1/Tp, форсирующее 1-го порядка - Tp ± 1, апериодическое 1-го порядка 1/(Tp ± 1), форсирующее 2-го порядка - (T2p2 ± 2ζTp + 1), апериодическое 2-го порядка - 1/( T2p2±2ζTp+1), при 1≤ζ или колебательное - 1/(T2p2±2ζTp+1), при 0<ζ<1.

Для каждого из звеньев могут быть найдены корни для уравнений, записанных в числителе или знаменателе, представляющих их передаточных функций. Корни уравнения, получаемого путем приравнивания нулю числителя передаточной функции (1) называются нулями, а корни уравнения, полученного приравниванием к нулю знаменателя (1) называют полюсами. Корни числителя – нули p0, знаменателя – полюса p*. Для отдельных звеньев корни будут иметь вид:

p

0*

= 0;

p

0*

= - 1/T; p

0*

=

ζ

ζ 2

− 1

;

−

±

,ζ ≥ 1

T

T

p0*

= −

ζ ± j cosϕ

,0 < ζ < 1.

(3)

T

По динамическим свойствам простейшие звенья могут быть подразделены на безынерционные, инерционные и звенья с запаздыванием.

Ряд звеньев называются элементарными, а именно безынерционные, идеально дифференцирующие и идеально интегрирующие.

Рассмотрим подробнее некоторые из звеньев.

1. Безынерционное звено (пропорциональное)

Уравнение динамики безынерционного звена имеет вид

y(t) = K x (t),

где K- коэффициент передачи (или усиления), который является постоянным для линейного звена.

Передаточная функция имеет вид:

W(р)=Y (р)/Х(р) = K;

Переходная характеристика звена

h(t) = L-1[W(p)/p] = L-1[K/p] = K·1(t)

Весовая функция пропорционального звена равна:

w(t) = L-1[W(p)] = K·δ(t)

Частотные характеристики (АФЧХ, АЧХ, ФЧХ и ЛАЧХ) звена:

W(jω) = K = K +0·j

A(ω) = K 2 + 0 2 = K

φ(ω) = arctg(0/K) = 0 L(ω) = 20·lg[A(ω)] = 20·lg(K)

2. Апериодическое звено первого порядка (инерционное)

Уравнение апериодического звена первого порядка имеет вид

T·dу/ dt + y = K·x,

где Т – постоянная времени, обусловленная наличием инерционных свойств элементов системы (масса, момент инерции, индуктивность, емкость и т.д.) и характеризующая продолжительность переходного процесса в ней;

K– коэффициент усиления (передачи).

Применяя преобразование Лапласа при нулевых начальных условиях, получим операторное уравнение

(Тр+1) Y( р) = K Х(р)

Из этого уравнения находится передаточная функция

W(р) = k/(1+Тр)

Переходная функция апериодического звена I-ого порядка имеет вид:

h(t) = L-1[W(p)·1(t)] = L-1[K/(p·(T·p + 1))] = K – K·e-t/T = K·(1 – e-t/T)

Весовая функция апериодического звена I-ого порядка имеет вид:

w(t) = L-1[W(p)] = L-1[K/(T·p + 1)] = (K/T)·e-t/T

АФЧХ, АЧХ, ФЧХ и ЛАЧХ апериодического звена I-ого порядка:

W(jω) = K/(T·jω + 1) = K·(T·jω – 1)/[(T·jω + 1)·(T·jω – 1)] =

= K·(T·jω – 1)/(-T2ω2 – 1) = K/(T2ω2 + 1) – [KTω/(T2ω2 + 1)]·j

K

2

−K T ω

2

K 2

(1+ T 2 ω 2 )

K

A(ω) =

+

=

=

(T 2 ω 2 + 1)2

T 2 ω 2 + 1

T 2 ω

2

+ 1

T 2 ω 2 + 1

−K

T

ω

(T

2

ω

2

+ 1)

ϕ (ω) = arctg

= arctg (−Tω) = −arctg (Tω)

(T 2 ω 2 + 1)

K

		K
L(ω) = 20 lg A(ω) = 20 lg					= 20 lg K −10 lg (T 2ω 2 + 1)
	T 2 ω 2
			+ 1

3. Апериодическое звено II-ого порядка

Апериодическое звено II-ого порядка описывается дифференциальным уравнением второго порядка:

(T1T2)·d2у(t)/dt2 + (T1 + T2)·dу(t)/dt + у(t) = K·х(t) .

Передаточная функция апериодического звена II-ого порядка имеет вид:

W(p) = K/[(T1·p + 1)·(T2·p + 1)],

где K – коэффициент усиления; T1 и T2 – постоянные времени, также характеризующие инерционность системы, т.е. продолжительность переходного процесса в ней. (T1 > 0 и T2 > 0).

Переходная характеристика апериодического звена II-ого порядка имеет вид:

h(t) = L-1[W(p)·1(t)] = L-1[K/[p·(T1·p + 1)·(T2·p + 1)]] =

=K·[1 – (T1/(T1 – T2))·e-t/T1 – (T2/(T2 – T1))·e-t/T2]

Вчастном случае, когда T1 = T2 = T аналитическое выражение для переходной характеристики имеет несколько иной вид:

h(t) = L-1[W(p)·1(t)] = L-1[K/[p·(T·p + 1)2]] = K·[1 – e-t/T – (t/T)·e-t/T]

Весовая функция апериодического звена II-ого порядка имеет вид:

w(t) = L-1[W(p)] = L-1[K/ [(T1·p + 1)·(T2·p + 1)]] =

=K·[(1/(T1 – T2))·e-t/T1 + (1/(T2 – T1))·e-t/T2] .

Вчастном случае, когда T1 = T2 = T аналитическое выражение для весовой функции имеет несколько иной вид:

w(t) = L-1[W(p)] = L-1[K/ (T1·p + 1)2] = (K·t/T2)·e-t/T .

Частотные характеристики (АФЧХ, АЧХ, ФЧХ и ЛАХ) апериодического звена II-ого порядка имеют вид

K (1 − T T ω 2 )

K ω (T + T )

W ( jω ) =

1

2

− j

1

2

(1 + T 2

ω 2 ) (1 + T 2

ω 2 )

(1 + T 2

ω 2 ) (1 + T 2

ω 2 )

1

2

1

2

A(ω ) =

K

(1 + T 2

ω 2 ) (1 + T 2

ω 2 )

1

2

ω

(T1

+ T2 )

ϕ (ω ) = −arctg

1 − T1 T2 ω 2

L(ω ) = 20 lg(K ) − 10 lg (1 + T

2 ω 2 ) − 10 lg (1 + T 2

ω 2 )

1

2

4. Колебательное звено

Колебательное звено описывается дифференциальным уравнением второго порядка:

T2·d2у(t)/dt2 + 2T ξ·dу(t)/dt + у(t) = K·х(t)

Передаточная функция колебательного звена имеет вид:

W(p) = K/[T2·p2 + 2T·ξ·p + 1],

где K – коэффициент передачи (усиления); T – постоянная времени, характеризующая инерционность системы, т.е. продолжительность переходного процесса в ней. (T > 0); ξ – коэффициент затухания (демпфирования), который характеризует рассеяние энергии в звене (0 < ξ < 1). При ξ≥ 1 колебательное звено превращается в апериодическое звено II - го порядка.

Переходная характеристика колебательного звена имеет вид:

h(t) = L-1[W(p)/p)] = L-1[K/[p·(T2p2 + 2T ξp +1)]] =

ξ t

1− ξ

2

ξ

1− ξ

2

= K 1− e−

T

cos

t +

sin

t

T

T

1 − ξ

2

Переходная

функция

имеет

достаточно сложный

вид,

но

наиболее

характерно то, что имеется экспоненциальное затухание переходного процесса с коэффициентом - ξ/T, а также колебательность с частотой

ωк	=		1− ξ 2
					.
			T
		Здесь важно отметить, что частота зависит от коэффициента затухания.
При ξ → 0				ωк → 1/T; при ξ → 1 ωк → 0.

Весовая функция колебательного звена имеет вид:

w(t) = L-1[W(p)] = L-1[K/(T2p2 + 2T ξ p +1)] =

	K e−		ξ t
							1− ξ 2
			T
=						sin				t
	T 1− ξ			2				T

Частотные характеристики колебательного звена имеют следующий вид:

W(jω) = K/(T2·(–jω)2 + 2T ξ ·jω + 1) =

=

K − KT 2ω 2

− j

2KξTω

= U (ω) + j V (ω)

(1− T 2ω 2 )2 + 4ξ 2T 2ω 2

(1− T 2ω 2 )2 + 4ξ 2T 2ω 2

K

A(ω) = U (ω)2 + V (ω)2

=

(1− T 2ω 2 )2 + 4ξ 2T 2ω 2

V (ω)

2ξTω

ϕ (ω) = arctg

= −arctg

2

2

U (ω)

1 − T ω

L(ω) = 20 lg [ A(ω)]

=

2

2

)

2

2

2

2

20 lg K −10 lg (1

− T ω

+ 4ξ T ω

Принципиальное отличие ЛАХ колебательного звена от ЛАХ инерционных звеньев состоит в том, что в районе сопрягающей частоты ωс = 1/T имеется максимум (так называемый "горб"), из-за чего поведение асимптотической ЛАХ в этой области может существенно отличаться от истинной. Это явление называется резонансом. При этом максимум усиления амплитуды достигается при частоте:

ω

=

1 − 2ξ 2

A (ωmax ) =

K

и

max

T

,

2ξ

1− ξ

2 .

Как видно из приведенного выражения, резонанс в колебательном звене может возникнуть только при малых значениях ξ < 22 ≈ 0.707 , т.е. когда рассеяние энергии во внешнюю среду невелико.

5. Интегрирующее звено

Интегрирующее звено описывается дифференциальным уравнением первого порядка:

dу(t)/dt = K·х(t)

Передаточная функция интегрирующего звена имеет вид:

W(p) = K/p = 1/T·p,

где K – коэффициент усиления;

T – постоянная времени (время интегрирования); T = 1/K. Переходная функция интегрирующего звена имеет вид:

h(t) = L-1[W(p)/p] = L-1[K/p2] = K·t = t/T

Весовая функция интегрирующего звена имеет вид:

w(t) = L-1[W(p)] = L-1[K/p] = K·1(t) = (1/T)·1(t)

АФЧХ, АЧХ, ФЧХ и ЛАХ интегрирующего звена:

W(jω) = K/jω = Kω·j/ω2 = 0 – (K/ω)·j = 0 – (1/Tω)·j

A(ω) = 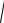0 2 + (−K ω ) 2 = K/ω = 1/T ω

φ(ω) = arctg(-(K/ω)/0) = –arctg(∞) = –π/2 = –900

L(ω) = 20·lg[A(ω)] = 20·lg(K/ω) = 20lg(K) – 20lg(ω) = –20 lg(Tω)

6. Дифференцирующее звено

Дифференцирующее звено описывается уравнением производной от входного сигнала:

у = T·dх(t)/dt

Передаточная функция дифференцирующего звена имеет вид:

W(p) = T·p,

где T – постоянная времени (время дифференцирования).

Поскольку идеальное дифференцирующее звено физически нереализуемо, при этом сама операция дифференцирования часто встречается при описании

процессов разной природы, то на практике часто используют "нетиповое"

реальное дифференцирующее звено. Реальное дифференцирующее звено является соединением двух типовых звеньев - идеального дифференцирующего и инерционного, которые вместе приближённо описывают операцию дифференцирования. Передаточная функция реального дифференцирующего звена имеет вид:

W(p) = T1p/(T2p + 1),

где T1 – постоянная времени дифференцирующей составляющей (время дифференцирования), а T2 – постоянная времени апериодической составляющей. При малых значениях T2, т.е. когда инерционность апериодического звена мала, составляющей T2p в знаменателе передаточной функции можно пренебречь, тогда мы получим приближенную передаточную функцию идеального дифференцирующего звена:

W(p) = T1p/(T2p + 1) ≈ T1p.

Такое звено хорошо работает при низких частотах. Максимальная частота, при которой реальное дифференцирующее звено еще работает "почти как идеальное" равна:

ω = 1/T2.

Переходная функция дифференцирующего звена

h(t) = L-1[W(p)/p] = L-1[T] = T·δ(t)

Весовая функция дифференцирующего звена

w(t) = L-1[W(p)] = L-1[T·p] = T·dδ(t)/dt

Частотные характеристики

W(jω) = T·j·ω = 0 + Tω·j

A(ω) = Tω

φ(ω) = arctg(Tω/0) arctg(∞) = π/2

L(ω) = 20lg[A(ω)] = 20lg(Tω).

Задание:

1.Используя навыки, полученные при выполнении практических заданий № 3 и № 4, найти аналитические выражения для динамических характеристик типовых звеньев САУ: временных - весовую функцию w(t), переходную функцию h(t) и частотных - АФЧХ, АЧХ, ФЧХ, ЛАЧХ, ЛФЧХ.

2.Построить при помощи компьютерной программы MATHCAD и вывести на печать графики характеристик, найденных при выполнении п. 1 задания.

3.Передаточную функцию W(p), соответствующую типу звена выбрать из табл. 1.

Таблица 1

1

2

3

4

5

k

k

k

1

T1 p

T p +1

T 2 p 2

+ T p + 1

T p

T p +1

2

1

2

Пропорци-

Инерционное

Апериодическое

Интегри-

Реальное

ональное

II – го порядка

рующее

дифферен-

цирующее

4. При вычислениях использовать варианты параметров типовых звеньев из табл. 2, в соответствии с последними цифрами шифра студента.

Таблица 2

Параметры				Номер варианта
звена	1	2	3	4	5	6	7	8	9	0
К	5	10	8	6	4	9	2	3	7	1
T=Т1	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
T2	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1

Методические указания к выполнению задания:

1.Перед выполнением задания ознакомиться с основными определениями и аналитическими выражениями из раздела «Краткие теоретические сведения».

2.Ознакомиться с заданием к практическому занятию и выполнить п. 1 задания.

3.Выполнить пункт 2 задания, используя MATHCAD и задавшись соответствующими масштабами по осям функции и аргумента для построения динамических характеристик типовых звеньев.

4.Оформить отчет, который должен содержать:

-название и цель практического занятия;

-основные определения и расчетные формулы;

-графики динамических характеристик (см. Приложение);

-выводы.

Примечание:

В приложении приведены в качестве примера графики временных и частотных характеристик инерционного звена.

Приложение

Временные характеристики
W(s) :=	K	K := 1		T := 0.2		W(s) :=	1
	T s + 1						0.2 s + 1
w(t) := 5 e− 5 t		h(t) := 1 − e− 5 t			t := 0 , 0.01.. 1
	График весовой функции
	5
	4
	3
	w ( t)
	2
	1
	0
	0	0.2	0.4	0.6	0.8	1
				t
		График переходной функции
	1
	0.8
	0.6
	h( t)
	0.4
	0.2
	0
	0	0.2	0.4	0.6	0.8	1
				t