2.2. Алгебра событий

Поскольку при теоретико-множественном подходе к теории вероятностей события отождествляются с множествами, то над событиями можно совершать те же самые операции, что и для множеств. В частности:

Алгебра событий		Алгебра множеств
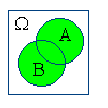
AB	событие А влечет за собой событие В		AB	множество А является подмножеством множества В
A=B	событие А тождественно событию В		A=B	равенство множеств
A+B	сумма событий, означающее, что произошло хотя бы одно из двух событий		AB	объединение множеств
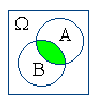
AB	произведение событий, означающее, что оба события произойдут одновременно		AB	пересечение множеств
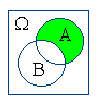
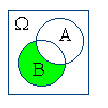
A–B	разность событий, означающее, что произойдет событие А, но не произойдет событие В		A \ B	разность множеств, т.е. мно­жество элементов, принадлежащих А, но не принадлежащих В
=–A	противоположное событие, означающее, что событие А не произойдет		= \ A	дополнение множества А до 

Если события А и В несовместны, то АВ=; если события А₁, А₂, ..., А_k образуют полную группу, то А₁+А₂+...+А_k =. В частности, противоположные события A и несовместны, т.е. А=, и образуют полную группу, т.е. А+=

Действия над событиями становятся более наглядными, если придать им геометрическую интерпретацию в виде диаграмм Вьенна:

A+B	AB	A–B	B–A	

Пример 2.2. Эксперимент состоит в подбрасывании двух игральных костей. Обозначим через X сумму очков, выпадавших на обоих костях. Пространство элементарных событий такого эксперимента можно записать в виде ={2;3;4;5;6;7;8;9;10;11;12}. Описать следующие события A+B, AB, A–B, B–A, если A={X кратно трем}={3;6;9;12}и B={X нечетно}={3;5;7;9;11}. Тогда

A+B={3;5;6;7;9;11;12},	A–B={6;12},
AB={3;9},	B–A={5;7;11}.

Пример 2.3. Пусть имеется колода карт, из которой вынимается одна карта. Описать события AB, B, A+B, A–B, если A={вынутая карта – туз}, B={вынутая карта – черви}.

Ответ:

AB={вынутая карта – червовый туз},

B={вынутая карта – червовая, но не туз },

A+B={ вынутая карта – либо туз, либо черви},

A–B={ вынутая карта –туз, но не черви}.

Пример 2.3. Пусть A, B, C – три события, наблюдаемые в некотором эксперименте. Используя алгебру событий, описать следующие события: а) произошло только событие А; б) произошло одно событие; в) произошло хотя бы одно событие.

Ответ:

а) ,

б) ,

в) A+B+C = .

Операции сложения (объединения) и умножения (пересечения) события обладают рядом свойств, аналогичных свойствам обычных операций над числами:

1а. A+B = B+A,	1б. AB = BA,
2а. A+(B+C) = (A+B)+C,	2б. A(BC) = (AB)C.

Это свойства коммутативности и ассоциативности. При этом, пустое множество  и само базисное множество  аналогичны нулю и единице, соответственно:

3а. A+ = A,

3б. A = A.

Однако некоторые свойства не имеют аналогов в обычных операциях над числами; в частности:

4а. A+A = A,

4б. AA = A.

Это свойства идемпотентности. При введении операций всегда возникает вопрос, какая из двух операций больше "похожа" на сложение, а какая на умножение. Ответ на этот вопрос дают свойства дистрибутивности. Однако для алгебры событий (соответственно, и для алгебры множеств) удивительным образом выполняются оба свойства дистрибутивности:

5а. (A+B)C = AC+BC,

5б. (AB)+C = (A+C)(B+C).

В теоретико-множественной трактовке эти свойства выглядят более симметрично:

5а. (AB)C = (AC)(BC),

5б. (AB)C = (AC)(BC).

Эти равенства характеризуют принцип двойственности алгебры событий и показывают равноправие обоих операций. Так, если будет доказана истинность какого-либо тождества, то истинным будет и двойственное ему тождество, т.е. то, которое получается из данного взаимной заменой символов «+» и «» (или «» и «»), а также  и . Поэтому все приводимые равенства сгруппированы в пары. Запишем еще несколько свойств:

6а. (AB)+A = A,	6б. (A+B)A = A,
7а. A+ = ,	7б. A = ,
8.  = A,
9а.  = ,	9а.  = ,
10а. A+ = ,	10б. A = ,
11а. ,	11б. .	Законы де Моргана

Система подмножеств множества , обладающая приведенными свойствами, называется булевой алгеброй. К булевым алгебрам относятся алгебра множеств, алгебра событий и алгебра логики.

Пример 3.4. Покажите, что события A, и образуют полную группу несовместных событий.

Решение. Покажем, что сумма данных событий образует достоверное событие. Используя законы де Моргана и другие свойства событий, получим:

.

Следовательно, данные события образуют полную группу. Чтобы доказать несовместность данных событий, найдем их попарные произведения:

,

,

.

Таким образом, данные в задаче события попарно несовместны. Следовательно, эти события образуют полную группу несовместных события, т.е. образуют пространство элементарных событий.